1. Introduction

In modern science and engineering, chaos and fractal theory have emerged as vital tools for understanding the behavior of complex systems. The phenomenon of chaos, first observed in meteorology and physics, reveals that even in seemingly deterministic systems, minute variations in initial conditions can lead to vastly different outcomes, highlighting the sensitivity and unpredictability inherent in such systems. Fractal theory, introduced by Benoît Mandelbrot in the 1970s, emphasizes the ubiquity of self-similarity and complex structures in nature. Fractals hold immense significance not only within the realm of geometry but also in a wide array of fields such as biology, image processing, and geographic information systems. Through the lens of fractal geometry, we can better describe and analyze nonlinear and complex phenomena found in nature. In recent years, the intersection of chaos and fractal research has garnered increasing attention from scholars and researchers. Numerous studies have demonstrated that the fractal characteristics of chaotic systems can provide profound insights into their dynamic behavior. For instance, chaotic attractors often exhibit intricate fractal structures, which not only influence the stability of the system but also have a profound impact on the predictability of its long-term behavior. Therefore, a deep and rigorous analysis of the relationship between chaos and fractals is imperative, as it contributes to unveiling the inherent laws and underlying mechanisms of complex systems, ultimately advancing our understanding of these systems and their behavior.

From the Chaos, Dynamics, and Fractals, people can get a basically knowledge of them [1]. Chaos system, in the mathematical context, refers to a deterministic system that exhibits seemingly random and irregular motion, characterized by uncertainty, non-repeatability, and unpredictability [2]. This phenomenon, known as chaos, is an inherent trait of nonlinear dynamical systems. A chaos system is a nonlinear dynamical system that displays chaotic behavior, meaning its long-term dynamics are highly sensitive to initial conditions and exhibit complex, unpredictable patterns despite being governed by deterministic rules.

At the heart of chaos theory lies the exploration of how even the simplest mathematical systems can generate complex and seemingly unpredictable behaviors over time. These systems are inherently nonlinear, meaning that the output is not proportional to the input, and minor variations in initial conditions can lead to vastly divergent outcomes over time.

This paper employs a literature review method to analyze the connection between chaos and fractals, delving into their similarities through a rigorous and systematic methodology. By examining existing research and theoretical frameworks, the paper aims to advance the theoretical development of chaos and fractals, exploring the intricate relationships and underlying mechanisms that govern their behavior. Furthermore, this paper seeks to bridge the gap between theoretical understanding and practical application, with the ultimate goal of better applying these concepts to real-life situations and harnessing their potential to solve complex problems in various domains.

2. Chaos

A defining characteristic of chaotic systems is their coexistence of order and disorder. While their behavior may seem random and unpredictable in the long run, they often exhibit underlying patterns and structures that can be uncovered and analyzed using mathematical tools.

Chaos theory finds widespread applications across various disciplines, including physics, biology, economics, and engineering. For instance, in meteorology, chaos theory offers insights into why long-term weather forecasting is inherently limited due to the extreme sensitivity of weather systems to initial conditions. Similarly, in biology, chaos theory has been employed to study the dynamics of population growth and the stability of ecological systems.

And the key characteristics of chaotic systems are as follows. First is aperiodicity. Chaotic systems do not exhibit regular or periodic behavior. Instead, their dynamics fluctuate in a seemingly irregular and unpredictable manner, lacking the strict repetition found in periodic systems. Secondly, chaotic systems are characterised by boundedness. Despite their apparent randomness, chaotic systems typically remain confined within a finite region of the state space. This implies that the system's variables do not diverge to infinity or converge to a single point, but rather fluctuate within well-defined boundaries. In some cases, chaotic systems display fractal patterns, where similar structures repeat themselves across different scales. This self-similarity contributes to the complex and intricate nature of chaotic dynamics. In addition, chaotic systems bear the hallmarks of long-term unpredictability and short-term predictability. Due to the butterfly effect, long-term predictions of chaotic systems are practically impossible. However, within a relatively short time frame, the system's behavior can be accurately predicted using mathematical models and numerical simulations [3]. Deterministic Chaos, despite its apparent randomness, arises from deterministic systems governed by precise mathematical rules. This paradoxical nature of deterministic chaos underscores the intricacies of nonlinear dynamics.

In summary, chaos is characterized by its extreme sensitivity to initial conditions, aperiodic behavior, boundedness within a state space, potential fractal self-similarity, long-term unpredictability, short-term predictability, and its origin in deterministic systems.

3. Fractals

Fractal, a mathematical concept coined by Benoît B. Mandelbrot in 1975, refers to geometric shapes or patterns that exhibit self-similarity across different scales.[4]

Therefore, fractals are an effective mathematical tool for describing complex structures in nature, revealing the self-similarity and structure in nature, and providing us with a new perspective to examine and understand the world. And the Key Characteristics of Fractal can be regarded as Self-Similarity. A fractal is characterized by its self-similarity, which means each part of the fractal resembles the whole, at least approximately, when viewed at a different scale. This property is either exact, statistical, or semi-self-similar.

4. Non-Integer Dimension

Fractals are often described using non-integer dimensions, known as fractal dimensions. This contrasts with traditional Euclidean geometry where objects have integer dimensions (e.g., 0 for a point, 1 for a line, 2 for a plane, and 3 for a solid).

Fractals are typically considered infinitely complex, as they contain detailed structures at arbitrarily small scales. This complexity is captured by their fractal dimension, which quantifies the "roughness" or "complexity" of the shape. Moreover, many fractals can be generated through recursive algorithms or iterative processes, where a simple rule is repeatedly applied to generate increasingly complex patterns.

5. Mandelbrot set

As a classic example of a fractal, the Mandelbrot set is a set of complex numbers for which the iterative function Zn+1 = Zn² + C remains bounded in absolute value [3]. Its boundary displays intricate self-similar patterns.

Mandelbrot sets exhibit complex structures that are similar to the whole when zoomed in locally. This self-similarity is particularly evident from a statistical perspective, where different scales of magnification reveal similar patterns and details. This characteristic makes Mandelbrot a classic example of fractal geometry and chaos theory, as shown in Figure 1.

Figure 1: The Mandelbrot Set [5]

Lorenz attractor is a system of ordinary differential equations first studied by mathematician and meteorologist Edward Lorenz while studying atmospheric convection problems, and it is the original of the chaos, and we found that the typical chaos system seemed to have some relationship with the key character of fractals [6].

Although the Lorenz attractor does not strictly follow the mathematical definition of self-similarity (as it is not a strict fractal structure), it exhibits self-similarity characteristics to some extent. As shown in Figure 2, specifically, the trajectories of Lorenz attractors exhibit complex winding and folding structures in phase space, which may exhibit similar shapes at different time scales and in different regions of phase space. Although this similarity is not strictly mathematical self-similarity, it reflects the inherent laws of complex structures in chaotic systems.

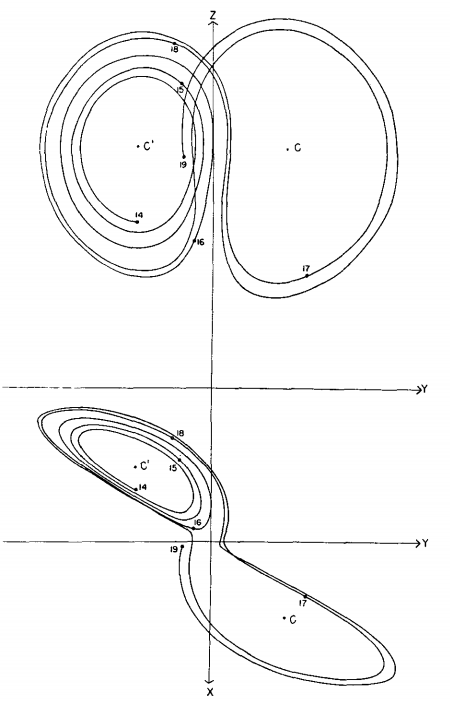
Figure 2: Numerical solution of the convection equations [6]

From the perspective of chaos theory, fractal structure can be regarded as the stable performance of chaotic systems under certain specific conditions. In the phase space of chaotic systems, the system state may evolve along complex trajectories, forming various attractor structures. When these attractor structures have fractal characteristics, it means that the system can exhibit similar complex structural patterns at different time scales. This self-similarity not only reflects the inherent regularity of chaotic systems, but also provides us with new perspectives and methods for understanding and predicting the behavior of complex systems.

The mathematical concepts of fractals and chaos have a profound impact on various fields beyond mathematics, fostering interdisciplinary developments and enhancing our understanding of complex systems. Here's a detailed exploration of their relationship and its implications for other domains:

The connection between the mathematical concepts of fractal and chaos lies in their shared exploration of complex, nonlinear systems that exhibit intricate patterns and unpredictable behavior. Fractals describe geometric shapes that repeat themselves at different scales, displaying self-similarity across various magnifications. Chaos theory, on the other hand, studies systems that are highly sensitive to initial conditions, resulting in unpredictable long-term behavior despite appearing to follow deterministic rules.

6. Impact on Other Fields

In Science and Engineering, firstly, fractals and chaos theory have helped explain phenomena such as turbulence, fluid dynamics, and quantum mechanics. They provide tools for modeling and predicting complex behaviors from the perspective of physics. And applications in engineering include chaos control in communication systems, chaos synchronization for secure transmissions, and fractal geometry for optimizing structures and materials.

In the field of Biology and Medicine, fractals and chaos theory shed light on biological structures and medical imaging. Many natural structures, like blood vessels, lungs, and neurons, exhibit fractal-like properties. These insights aid in understanding biological processes and disease mechanisms. And techniques like fractal analysis are used to detect abnormalities in medical images, enhancing diagnostic accuracy.

In Economics and Finance, chaos theory helps explain the seemingly random fluctuations in financial markets, revealing underlying patterns and predictability within chaos. And fractal analysis can be applied to assess market volatility and risk, informing investment strategies.

In Computer Science and Data Analysis, fractal-based algorithms are used for data compression, image processing, and network design, optimizing performance and efficiency. And chaos theory inspires novel data visualization techniques that reveal hidden patterns and correlations in complex datasets.

In Art and Design, artists harness fractal geometry to create intricate, visually stunning images and installations in the form of fractal art. And chaos theory informs design principles that embrace complexity and uncertainty, leading to innovative products and experiences.

The relationship between fractals and chaos transcends mathematics, driving advancements in diverse fields from physics to finance, biology to computer science. Their interdisciplinary applications underscore the power of these concepts in illuminating the intricacies of our world and fostering innovation across domains.

7. Conclusion

In summary, using chaos methods to explain fractals, we can consider fractals as stable structural representations of chaotic systems under certain specific conditions, which exhibit self-similarity and are influenced by nonlinear dynamical systems. Chaos and fractals, as two important concepts in nonlinear science, are closely related and interact with each other, jointly revealing the inherent laws and essential characteristics of complex systems.

This paper explores the relationship between chaos and fractals solely through literature review and computational derivation, lacking specific experimental verification and deep research, which constitutes a major flaw. To address this deficiency, future research can delve into the simulation of specific models and computational experiments, allowing for more intuitive observation and verification of the interactions and manifestations between chaos and fractals.

Simultaneously, linking chaos and fractal theory with other domains in life is also an important direction for research. It involves exploring the presence of chaotic properties in different fields and attempting to explain and predict these phenomena using the theories and methods of chaos and fractals. For instance, in domains such as physics, chemistry, biology, and economics, there may be hidden laws of chaos and fractals worth delving into.

Notably, the author believes that the field of chaos and fractals has great potential in predicting collective behavior. Due to the similarities between them, it may be possible to utilize the connection between chaos and fractals to predict the actions of extremely large sample populations. This interdisciplinary exploration is expected to provide new perspectives and methods for social science and complex systems research, driving the development and application of related fields.

In summary, future research should focus on experimental verification, deep simulation of specific models, and integrating chaos and fractal theory with other disciplines to discover more applications and values. Additionally, exploring the application of chaos and fractals in predicting collective behavior and other domains is also a worthwhile direction to pursue.