1. Introduction

With the development of global agriculture and increasing environmental pressure, optimizing crop planting strategies has become the key to improving agricultural productivity and achieving sustainable development [1]. In areas with variable geographical environments and complex climatic conditions, such as the mountainous areas of northern China, strategically planning crop planting can maximize the use of limited land resources and thus promote sustainable growth of the rural economy [2]. Effective crop planting optimization is not just about increasing yields; it also includes cost control, maximizing benefits, and reducing market risks. Traditional crop planting optimization methods, including linear programming, dynamic programming, and heuristic algorithms, have been widely used [3][4][5]. However, as the complexity of these problems increases with multidimensional constraints, traditional methods often have difficulty in getting rid of local optimality and lack sufficient global search capabilities. Recently, quantum genetic algorithms (QGAs) [6] have attracted attention for their global search capabilities and fast convergence. By incorporating quantum principles such as superposition, qubits, and revolving gates into classical genetic algorithms, QGAs excel in solving complex optimization problems. Its powerful global search capability effectively prevents premature convergence, making it highly applicable in agricultural optimization. Optimizing crop planting strategies involves many uncertainties, including market demand fluctuations, climate change, and rising production costs [7]. In addition, the substitutability and complementarity of crops also affect planting decisions.

In this study, we propose a crop planting optimization model based on quantum genetic algorithm. By considering various uncertainties (including market demand fluctuations, climate change, and rising production costs) as well as the substitutability and complementarity of crops, we aim to create a more adaptive and resilient planting strategy. The proposed model combines single-objective and multi-objective optimization, using an improved version of QGA to strike a balance between maximizing expected profits and minimizing risks. With this approach, we aim to optimize crop planting strategies and improve agricultural decision-making efficiency.

2. Method

2.1. Quantum Genetic Algorithm (QGA)

The Quantum Genetic Algorithm (QGA) is an optimization method that combines the characteristics of quantum computing with classical genetic algorithms. Compared to traditional genetic algorithms, QGA introduces concepts from quantum computing, such as qubits and rotation gates, enhancing its global search ability and convergence speed. In QGA, an individual’s gene encoding is represented by qubits, each of which can simultaneously represent a superposition of states 0 and 1, significantly increasing the diversity of the solution space and the robustness of the algorithm. In the implementation of QGA, each chromosome is composed of multiple qubits, with the state of each qubit represented by the probability amplitudes \( α \) and \( β \) :

\( |Ψ⟩=α|0⟩+β|1⟩, where {α^{2}}+{β^{2}}=1 \) (1)

The superposition property allows each qubit to exist in both 0 and 1 states simultaneously, thereby providing a larger search space. QGA mainly consists of the following key steps: quantum state initialization, quantum rotation gate operation, fitness calculation, and quantum measurement.

In crop planting strategy optimization, QGA has significant advantages. We apply QGA to optimize crop planting strategies, exploring optimal planting plans under various constraints and uncertainties. Based on this, the QGA algorithm is further improved to meet multi-objective optimization requirements, constructing an optimization model based on the Multi-Objective Quantum Genetic Algorithm (MO-QGA).

2.2. Single-Objective Optimization

In the optimization model, we assume that market demand, planting costs, yield per acre, and sales prices for various crops remain unchanged from 2023. Therefore, we first construct a single-objective optimization model with the goal of maximizing profit to formulate an optimal crop planting plan. The model considers two scenarios: (1) surplus production cannot be sold, resulting in losses, and (2) surplus production is sold at a discounted price.

In scenario 1 (where surplus production cannot be sold), the objective function is to maximize planting revenue, calculated as follows:

\( Max {Z_{1}}=\sum _{t=2024}^{2030}\sum _{n}\sum _{m}\sum _{q=1}^{2}({P_{m}}×min{( {Q_{m}}×{X_{m,n,t,q}},{S_{m}})}-{C_{m}}×{X_{m,n,t,q}}) \) (2)

where \( {P_{m}} \) is the sales price of crop \( m \) , \( {Q_{m}} \) is the yield per acre, \( {S_{m}} \) is the expected sales volume, and \( {C_{m}} \) is the planting cost. \( {X_{m,n,t,q}} \) represent the planting area (in acres) of crop \( m \) on plot \( n \) in year \( t \) and quarter \( q \) . \( {Y_{m,n,t,q}} \) represent a 0-1 variable indicating whether crop \( m \) is planted on plot \( n \) in year \( t \) and quarter \( q \) .

In scenario 2 (where surplus production is sold at a 50% discount), the objective function is:

\( Max {Z_{2}}=\sum _{t=2024}^{2030}\sum _{n}\sum _{m}\sum _{q=1}^{2}( \begin{array}{c} {P_{m}}\cdot min{({Q_{m}}\cdot {X_{m,n,t,q}},{S_{m}})} \\ +0.5\cdot {P_{m}}max{(0,{Q_{m}}\cdot {X_{m,n,t,q}}-{S_{m}})}-{C_{m}}\cdot {X_{m,n,t,q}} \end{array} ) \) (3)

The constraints include: The total planting area on each plot cannot exceed the plot's area.

\( \sum _{m}\sum _{q=1}^{2}{X_{m,n,t,q}}≤{A_{n}}, ∀n,∀t \) (4)

Different types of crops and planting seasons are limited depending on the plot type. For example, on dryland plots, only one season of non-rice crops can be planted per year.

\( \sum _{m∈G}\sum _{q=1}^{2}{X_{m,n,t,q}}≤{A_{n}},∀n∈{J_{1}},∀t \) (5)

Each plot must grow legumes at least once every three years to improve soil quality.

\( \sum _{t=r}^{r+2}\sum _{q=1}^{2}\sum _{m∈B}{X_{m,n,t,q}}≥1,∀n,∀τ∈\lbrace 2024,⋯,2028\rbrace \) (6)

The single-objective optimization model is solved using QGA. By applying quantum superposition and rotation gates, QGA efficiently navigates the solution space to find the optimal planting strategy for both scenarios. The fitness function is evaluated at each generation, and quantum measurement is performed to derive the best solution.

2.3. Multi-Objective Quantum Genetic Algorithm (MO-QGA)

In practical crop planting strategy applications, a single objective is often insufficient to meet all requirements. To address multiple uncertainties, such as market demand, yield per acre, and planting costs, we constructs a multi-objective quantum genetic algorithm model (MO-QGA) with the goal of balancing profit and risk through multi-objective optimization. The multi-objective model primarily considers the following uncertainty factors. Uncertainty in Sales Volume: The sales volume of crop \( m \) in year \( t \) is \( {S_{m,t}}×{ξ_{S}} \) , where \( {ξ_{S}}∼U(0.95,1.05) \) . Uncertainty in Yield per Acre: The yield per acre of crop \( m \) in year \( t \) is \( {Q_{m,t}}×{ξ_{Q}} \) , where \( {ξ_{Q}}∼U(0.9,1.1) \) . Uncertainty in Planting Cost: The planting cost of crop \( m \) in year \( t \) is \( {C_{m,t}}×{ξ_{C}} \) , where \( {ξ_{C}} \) increases by 5% each year. Then, we use orthogonal experimental design to generate various uncertainty scenarios, with the dual objectives of maximizing expected profit and minimizing the worst-case profit. The objective functions for the multi-objective optimization model are:

\( Max {Z_{1}}=\frac{1}{K}\sum _{k=1}^{K}\sum _{t=2024}^{2030}\sum _{n}\sum _{m}\sum _{q=1}^{2}(P_{m,t}^{(k)}×min{( Q_{m,t}^{(k)}×{X_{m,n,t,q}},S_{m,t}^{(k)})}-C_{m,t}^{(k)}×{X_{m,n,t,q}}) \) (7)

\( Max {Z_{2}}={\underset{k∈\lbrace 1,2,…,K\rbrace }{min}{\sum _{t=2024}^{2030}\sum _{n}\sum _{m}\sum _{q=1}^{2}(P_{m,t}^{(k)}×min{( Q_{m,t}^{(k)}×{X_{m,n,t,q}},S_{m,t}^{(k)})}-C_{m,t}^{(k)}×{X_{m,n,t,q}})}} \) (8)

In the multi-objective model, the constraints must hold across all uncertainty scenarios. The constraints on plot area, crop combination, rotation, and intercropping are consistent with the single-objective model, but the multi-objective optimization model requires robustness across different scenarios. In this study, we use the improved MO-QGA to solve the above multi-objective optimization problem. MO-QGA, which incorporates the concepts of the Non-dominated Sorting Genetic Algorithm II (NSGA-II), achieves dual-objective optimization. During evolution, the MO-QGA can more effectively explore the global solution space through rotation and mutation operations of qubits. Non-dominated sorting is used to filter individuals that meet the Pareto optimality criteria, and quantum measurement converts quantum states into planting strategies, ultimately obtaining optimal planting plans under various uncertainty scenarios.

2.4. Crop Substitutability and Complementarity

In crop planting planning, the substitutability and complementarity relationships among different crops significantly impact profits. we calculate crop correlations using Pearson correlation coefficients and groups crops with similar characteristics through hierarchical clustering. Based on this, we introduce substitution variables to quantify substitution effects between different crops, constructing a multi-objective optimization model incorporating crop substitutability and complementarity.

The substitution variable \( {Z_{m1,m2,n,t,q}} \) represents the substitution effect between crops \( m1 \) and \( m2 \) on plot \( n \) , in year \( t \) , and quarter \( q \) , defined as follows:

\( {Z_{{m_{1}},{m_{2}},n,t,q}}∈[0,1] \) (9)

When \( {Z_{m1,m2,n,t,q}}=1 \) , crops \( m1 \) and \( m2 \) are fully substitutable; when \( {Z_{m1,m2,n,t,q}}=0 \) , they are not substitutable at all. Based on the substitutability analysis, the objective function includes comprehensive revenue and substitution benefits:

\( Max {Z_{1}}=\sum _{t=2024}^{2030}\sum _{n}\sum _{m}\sum _{q=1}^{2}({P_{m}}×min{( {Q_{m}}×{X_{m,n,t,q}},{S_{m}})}-{C_{m}}×{X_{m,n,t,q}})+\sum _{m1,m2}{α_{m1,m2}}×{Z_{m1,m2,n,t,q}} \) (10)

\( Max {Z_{2}}=\sum _{m1,m2}{β_{m1,m2}}×{Z_{m1,m2,n,t,q}}-{γ_{m1,m2}}×|{X_{m1,n,t,q}}-{X_{m2,n,t,q}}| \) (11)

The improved MO-QGA solves the multi-objective optimization model with substitutability and complementarity. Pareto optimal solutions with the best substitution benefits are selected using non-dominated sorting, and optimal crop combinations are derived.

3. Experimental analysis

In order to verify the effectiveness of the multi-objective optimization model under different planting strategy scenarios, we conducted an experimental analysis. The experimental data included the basic values of variables such as the market price, expected sales volume, per-acre yield, and planting cost of the target crop, which mainly came from the crop planting data in North China in the past five years. In the multi-objective scenario, we introduced crop complementarity analysis to examine the impact of different crop combinations on the optimization results.

3.1. Experimental results of the multi-objective quantum genetic algorithm (MO-QGA)

In the multi-objective scenario, we introduced uncertain factors such as market demand, yield and planting cost, and used MO-QGA to solve them, aiming to balance the expected return and the worst-case scenario return. The experimental results are shown in Figure 1. It shows the planting strategy in the multi-objective scenario from 2024 to 2030. In this scenario, the model not only considers high-yield crops, but also selects some low-risk crops (such as legumes) to reduce the risks brought by potential market fluctuations. Through multi-objective optimization, the model effectively strikes a balance between maximizing returns and minimizing risks, ensuring that relatively stable returns can be obtained even when market demand fluctuates drastically. In the multi-objective scenario, MO-QGA effectively utilizes the global search capability and multi-objective optimization strategy of quantum algorithms to ensure the stability of the model under multiple uncertainty scenarios. By generating multiple uncertainty scenarios through orthogonal experimental design, MO-QGA achieves the optimal balance between different objective functions. The results show that compared with the single-objective model, the multi-objective model has more advantages in total return and return stability.

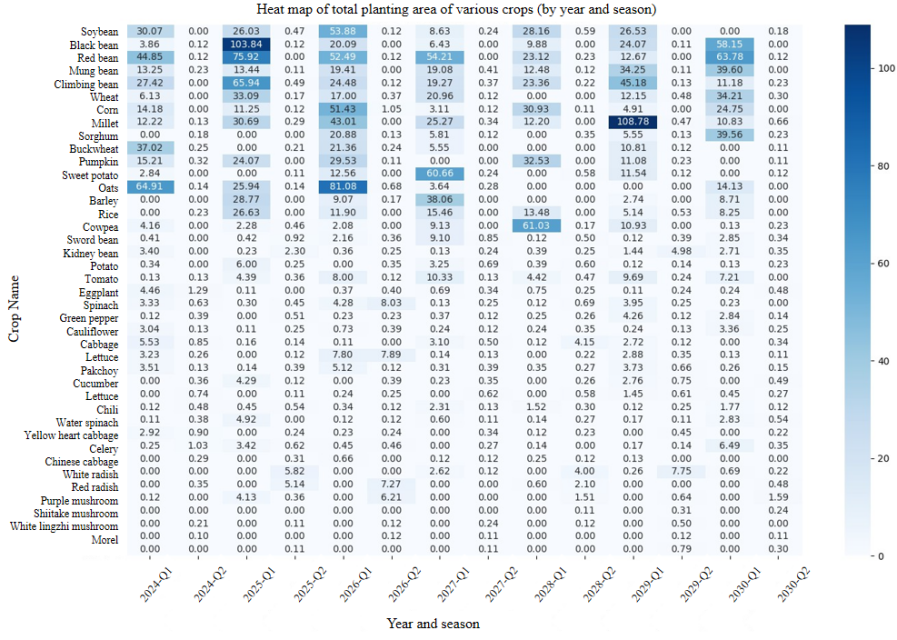
Figure 1: Heat map of optimal planting strategy under multi-objective scenarios

3.2. Complementarity analysis

In addition, we use a bottom-up evolutionary tree clustering method to perform cluster analysis based on characteristics such as crop planting cost, per-acre yield, expected sales volume, and average selling price, as shown in Figure 2. From the clustering results, crops are divided into several different clustering groups. Green group: including "wheat", "corn", etc. The planting cost and expected sales volume of these crops are relatively low, but the yield is high, which is suitable for scenarios with large planting areas. Blue group: including "cabbage", "lettuce", etc., characterized by high per-acre yield and planting cost, usually planted in greenhouses or greenhouses. Red group: There are many types of vegetables and fruits, such as "tomatoes", "eggplants", etc. These crops usually have medium planting costs, moderate expected selling prices and sales volumes, and are suitable for diversified planting.

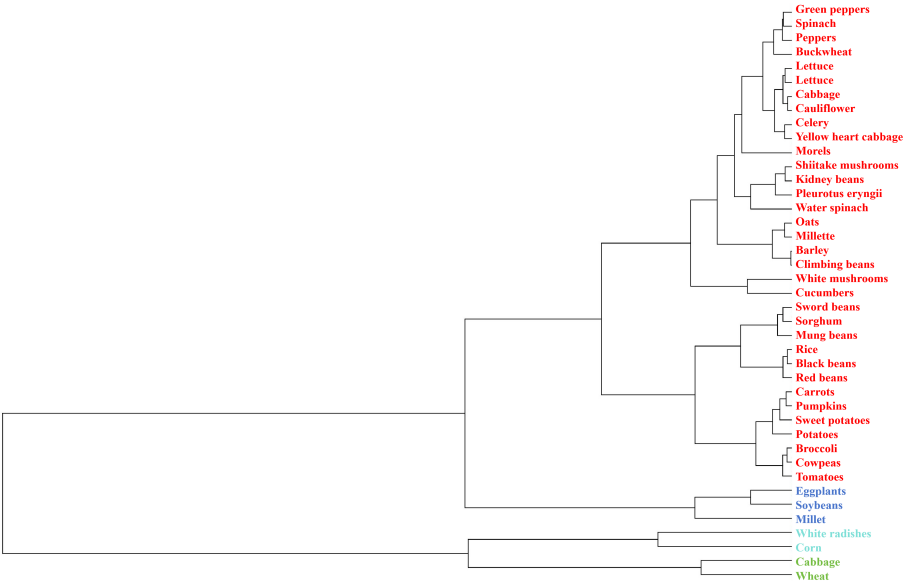
Figure 2: Cluster evolutionary tree diagram of crop characteristics

3.3. Comparative Experimental Analysis

In order to verify the advantages of the improved quantum genetic algorithm (QGA) in crop planting optimization, we designed a comparative experiment with the traditional genetic algorithm (GA) and particle swarm optimization algorithm (PSO). The experiment selected the same initial parameters and uncertainty scenarios, and used total revenue, convergence speed and algorithm stability as the main evaluation indicators to test the performance of the three algorithms under single-objective optimization (no sales and discount sales scenarios) and multi-objective optimization (market fluctuation scenarios).The results are shown in Table 1.

Table 1: Comparative analysis of this method with other traditional methods

The experimental results show that the improved QGA is superior to the traditional GA and PSO in total revenue and convergence speed. Especially in the multi-objective optimization scenario, QGA shows better stability with lower variance, which is suitable for dealing with complex uncertainty factors in agricultural planting.

4. Conclusion

In this study, we demonstrate the great potential of enhanced quantum genetic algorithm (QGA) for optimizing crop planting strategies under uncertain conditions. By combining single-objective and multi-objective optimization models, we show that QGA can effectively balance profitability and risk, providing an effective solution for modern agricultural decision-making. Compared with traditional optimization methods such as genetic algorithm and particle swarm optimization, the improved QGA outperforms them in terms of total benefits, convergence speed, and stability under multiple uncertain scenarios.