1. Introduction

Black holes are of enormous mass and gravity and thus serve an essential function in understanding the construction and evolution of the universe. According to general relativity, space and time are so curved by black holes that nothing can escape their gravitational pull, not even light, hence it has no color [1]. The concept started to take shape in the 18th century, drawing inspiration from the writings of some physicists, but it was Albert Einstein's theory that established the foundation for modern black hole physics [2].

In 1916, Karl Schwarzschild discovered the solution to Einstein's field equations pertaining to a static, spherically symmetric black hole, which is currently known as the Schwarzschild solution. These black holes, known as Schwarzschild black holes, possess mass but lack both spin and charge. In 1963 Roy Kerr gave an extension to his work by putting up a solution for rotating black holes: the Kerr black holes, which allowed angular momentum—the kind of characteristic that one expects for most astrophysical black holes [3].

Another important black hole under investigation by researchers is Sgr A*, a supermassive black hole founded at the center of the Milky Way galaxy [4]. Due to its significant influence on surrounding stars, Sgr A* serves as the optimal black hole for studying its properties and testing general relativity. Important insights into the structure of Sgr A* were derived from more recent Event Horizon Telescope (EHT) observations [5].

The central question that this paper tries to answer is whether or not Sgr A* should be considered to mimic more closely a Schwarzschild or a Kerr black hole. The author states that by computing its Schwarzschild radius and through other evidence—the topic of gravitational wave detections and outflow emissions—it can be established whether Sgr A* shows significant spin. This study enhances our comprehension the significance of black holes in the formation of the universe.

2. Literature Review

2.1. The Classification and Formation of Black Holes

2.1.1. Classification of Black Holes

Black holes are typically categorized based on their mass, spin, and charge. Among the common types are Schwarzschild black holes, which have neither charge nor spin [6]; Reissner-Nordström black holes, which are charged [7]; Kerr black holes, which possess spin but lack charge [8]; and Kerr-Newman black holes, which exhibit both spin and charge [9]. The Schwarzschild black hole is often viewed as an idealized model, while the Kerr black hole is considered more realistic, as most stars retain angular momentum prior to their collapse [10].

2.1.2. Formation of Black Holes

Black holes can arise through various mechanisms, primarily influenced by their mass. The most common way that stellar black holes are formed is at the conclusion of the life cycle of massive stars [11]. When a star exceeds 20 solar masses and exhausts its nuclear fuel, it loses the thermal pressure necessary to counteract gravitational collapse. As a result, the core of the star succumbs to gravitational force, and if the center's mass surpasses the limit [12] (approximately 2-3 solar masses), it will continue to collapse, ultimately resulting in the formation of a black hole.

The phases of this procedure typically include:

• Supernova Explosion: The star's outer layers are expelled as the core collapses inward.

• Formation of Neutron Stars or Black Holes: If the remnant core is massive enough, gravitational attraction triumphs over all other forces, resulting in black hole formation.

Exactly how supermassive black holes like those in quasars are actually formed is largely an area for active research today. A number of hypotheses have been put forward to describe their formation:

• Direct Collapse: Huge gas clouds in the early universe just fell into black holes without first forming stars.

• Accretion Growth: Formed from stellar implosions, small black holes could increase in size through time by merg­ing with others and accreting gas.

• Primordial Black Holes: According to some ideas, the gigantic mass black holes originated from variabilities in density within the rush minutes after creation with supermasses developing rapidly shortly after the Big Bang. Some theories suggest that supermassive black holes may have formed in the early universe, shortly after the Big Bang, as a result of density fluctuations in the primordial cosmic plasma.

2.2. General Relativity and Space-Time

In Einstein's general theory of relativity, gravity differs from the distant force that Newton conceptualized. Rather, it arises from the bending of space-time due to mass and energy. In this framework, the collapsed star exerts a pull on space-time itself. The event horizon, which marks the boundary for any matter that falls in, is not a tangible surface but rather the point beyond which no return is possible [13].

A fundamental concept of relativity is that light travels at a constant speed in a vacuum, which signifies the ultimate speed limit of the universe. This concept plays a crucial role in comprehending black holes. At the event horizon of a black hole, the speed required to escape exceeds that of light, indicating that nothing can break free, not even light.

2.2.1. Conservation of Light Speed and the Maximum Speed of Light

The core idea of Einstein's special theory of relativity was to address the discrepancies between Newtonian mechanics and Maxwell's electromagnetic theory, which asserted that the velocity of light stays the same. The well-known Michelson-Morley experiment [14] demonstrated this principle, revealing that light maintains a consistent speed irrespective of the observer's velocity. Illustrated in the light cone diagram below, it is determined that no signal or object can surpass the speed of light; at the heart of the idea of the event horizon lies the principle of a limit beyond which nothing can escape.

2.2.2. Equivalence Principle

The principle of equivalence indicates that the impacts of gravity cannot be differentiated from those caused by acceleration [15]. For instance, an observer in a closed box on earth would experience the same force as an observer in a box accelerating in gravity-free space. It is this principle that is crucial to the understanding of how objects behave near black holes: the very intense gravity that makes acceleration seem to mimic it.

It is this principle that allows the laws of special relativity to be applied in small regions of curved space-time. And this is essential in the black hole scenarios for solving Einstein’s field equations.

2.2.3. Curvature of Space-Time

The allocation of mass and energy is connected to the curvature of spacetime through the equations of Einstein field [16]. Near black holes, this curvature reaches extreme levels, resulting in effects like time dilation and gravitational lensing. There are three varieties of curvature: positive curvature, negative curvature, and zero curvature.

• Positive curvature: Space-time curves, which is equivalent to the surface of a sphere.

• Negative curvature: Space-time curves like a saddle.

• Zero curvature: Space-time is flat; that is, space-time has no intrinsic curvature.

At the singularity of black holes, space-time curvature reaches infinity, while the event horizon serves as the boundary where even light cannot escape. The Schwarzschild and Kerr metrics provide the geometric descriptions for static and spinning black holes, respectively.

2.3. Einstein Field Equations and Special Solutions

2.3.1. Equations of Einstein Field

The space-time curvature, represented by the Einstein tensor \( {G_{μν}} \) , is connected to the allocation of mass and energy, which is conveyed through the stress-energy tensor \( {T_{μν}} \) , according to the equations of Einstein field [17]. The general form of the field equation can be stated as:

\( {G_{μν}}={R_{μν}}-\frac{1}{2}{g_{μν}}R=\frac{8πG}{{c^{4}}}{T_{μν}} \) (1)

The curvature produced by the arrangement of mass-energy within space-time is represented by \( {G_{μν}} \) , while \( {T_{μν}} \) illustrates the elements of this distribution, including the energy and momentum associated with matter. The gravitational constant is denoted by G, and c is the light speed.

These equations imply that space-time bends when influenced by massive objects, and this curvature prescribes the paths along which other objects travel. In the absence of matter (in a vacuum), then \( {T_{μν}} \) = 0, the field equations reduce to much simpler forms allowing exact solutions to be found, such as the Schwarzschild and Kerr metrics.

2.3.2. Schwarzschild Solution

The Schwarzschild solution represents the easiest form of equations of Einstein's field, illustrating a static, uncharged black hole [18]. It is spherically symmetric and one of them represents a black hole whose only defining characteristic is mass. The final solution of Schwarzschild metric is indicated in the below equation:

\( {ds^{2}}=-(1-\frac{2GM}{r}){dt^{2}}+\frac{1}{1-\frac{2GM}{r}}{dr^{2}}+{r^{2}}({dθ^{2}}+{sin^{2}}θ{dϕ^{2}}) \) (2)

A key takeaway from the Schwarzschild solution is the Schwarzschild radius, defining the event horizon, marking the boundary beyond which no escape is feasible. The Schwarzschild radius, denoted as \( {r_{s}} \) , is expressed by:

\( {r_{s}}=\frac{2GM}{{c^{2}}} \) (3)

In this context, \( M \) represents the black hole mass, \( G \) denotes the gravitational constant, and \( c \) stands for the light speed. Anything that falls within the Schwarzschild radius will become a black hole.

2.3.3. Kerr Solution

The Kerr solution builds upon the Schwarzschild solution by taking into account rotating black holes [19]. This solution characterizes a black hole that possesses both mass and angular momentum, while excluding any charge or unusual attributes. The presence of an ergosphere complicates the metric for a Kerr black hole; this region exists beyond the event horizon, where the black hole's rotation pulls space-time along with it, a phenomenon also referred to as frame-dragging. The Kerr metric is explicitly expressed in relation to the spin:

\( a=\frac{J}{Mc} \) (4)

where \( J \) represents the angular momentum, \( M \) is the mass, and \( c \) is the speed of light. The Kerr solution is a more authentic representation for real astrophysical black holes since by virtue of the angular momentum from collapsing stars, most black holes are expected to spin. The final Kerr solution is:

\( {ds^{2}}=\frac{{r^{2}}-2Mr+{a^{2}}}{{ρ^{2}}}{(dt-a{ sin^{2}}θ dφ)^{2}}-\frac{{ρ^{2}}}{{r^{2}}-2Mr+{a^{2}}}{dr^{2}}-{ρ^{2 }}{dθ^{2}}-\frac{{({r^{2}}+{a^{2}})^{2}} {sin^{2}}θ}{{ρ^{2}}}{(dφ-\frac{a}{{r^{2}}+{a^{2}}}dt)^{2}} \) (5)

The key differences between Schwarzschild and Kerr black holes are:

• Event Horizon: In a Kerr black hole, the event horizon shrinks with increasing spin.

• Ergosphere: Unique to Kerr black holes, the ergosphere facilitates the retrieval of energy through the Penrose process.

3. Discussion

The properties of Sgr A* are detailed in the following subsection. Based on the observational data currently available, evidence suggests that Sgr A* is more probably a Kerr black hole rather than a Schwarzschild black hole. Additionally, this paper explores the alternative theory that Sgr A* might be considered an ideal Schwarzschild black hole—characterized by the absence of spin or charge—and examines how this model falls short in accounting for the observational data.

3.1. Observations of Sgr A*

Sgr A* was first recognized as a dense radio emitter in 1974 [20], several methods have since been developed to observe and analyze Sgr A*: infrared radiation, X-ray emissions, and most recently, gravitational wave detections [21].

In 2017, the Sgr A* obtained a photograph captured by the EHT, which was made public in the following years [22]. The image, shown in Figure 1, is of the accretion disk that surrounds the black hole horizon event. The Schwarzschild radius of Sgr A* defines the boundary beyond which nothing can escape, including information in the form of light. Matter crossing this event horizon is not observable to distant observers since signals from it would take an infinite time to reach them.

Some researchers at UCLA reported observing Sgr A* to be relatively stationary while surrounded by high-velocity orbiting stars, as shown in Figure 2 [23]. Prime ingredients for such estimates are observations of the type we have just described. It was determined from observational data that the mass of Sgr A* is estimated to be 4.1 × 10⁶ M_⊙. The mass was determined, in particular, from measurements of the velocities of orbiting stars.

Figure 1: Image of Sgr A* captured by the EHT in 2017 [22].

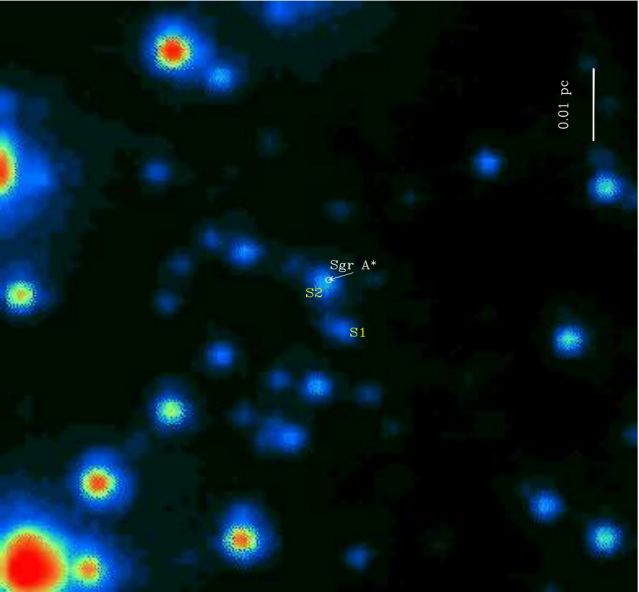
Figure 2: The position of Sgr A* [23].

3.2. Properties of Sgr A* as an Ideal Schwarzschild Black Hole

3.2.1. Measuring the Galactic Centre Mass by Stellar Orbitals

Whether Sgr A* can be entitled to represent an ideal Schwarzschild black hole or not, its mass should first be known. The most accurate way to measure Sgr A*’s mass is by investigating the orbits of stars located near the galactic center, in particular, S0-2 (or S2) because its orbit is well characterized. The paths of various stars orbiting Sgr A* are shown in Figures 3 and 4; these were data as collected by Ghez et al. [24].

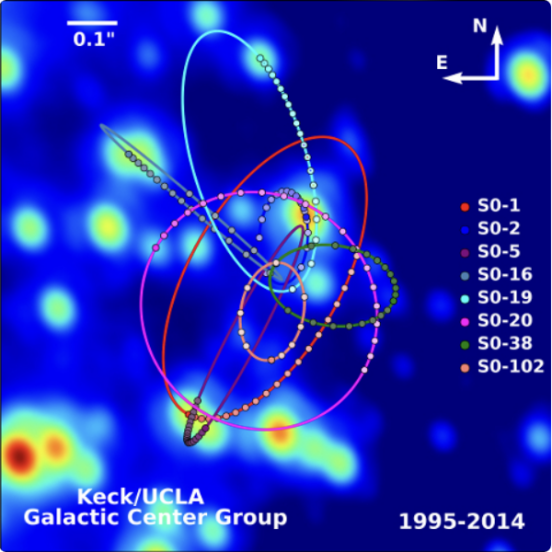
Figure 3: Orbits of stars near Sgr A* [25].

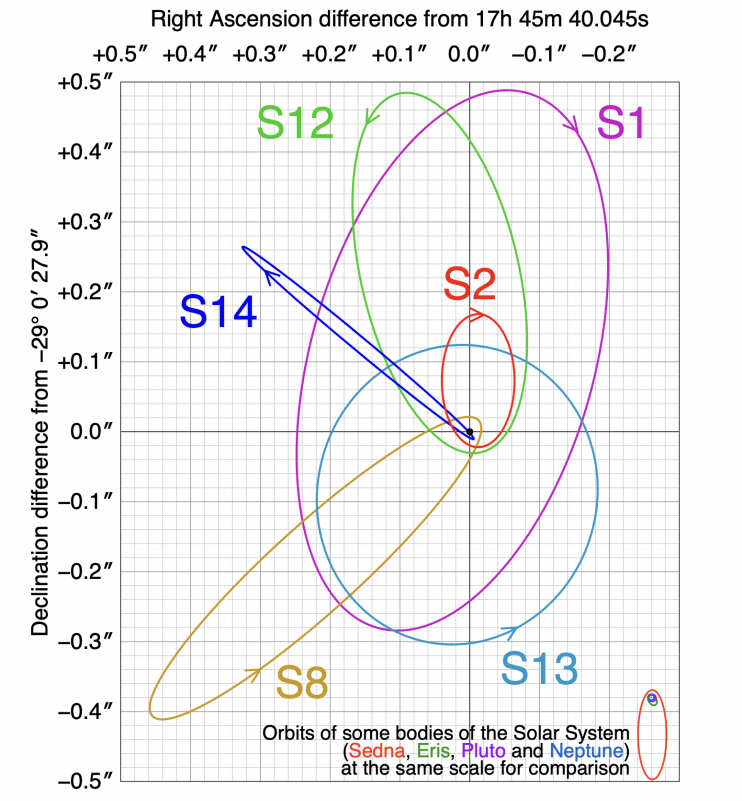
Figure 4: Stellar orbits in coordinate system diagram [26].

The Sgr A*’s mass can be calculated by applying the third law of Kepler [27]. The timeframe of S0-2’s orbit is approximately 15.6 years, with a periapse distance of around 120 AU. The eccentricity of the orbit is about 0.88. See Table 1.

Table 1: Parameters for S0-2 [24].

Based on the third law of Kepler, the calculation of semi-major axes can be performed as follows:

\( a=\frac{120}{1-0.88}=1000 AU \) (6)

The mass of Sgr A* ( \( {M_{Sgr A*}} \) ) is then determined using the equation:

\( {M_{Sgr A*}}=\frac{{1000^{3}}}{{15.6^{2}}}=4.109×{10^{6}}{ M_{⨀}}≈{4.1×10^{6}}{ M_{⨀}} \) (7)

This mass value aligns with previous estimates and allows the calculation of Sgr A*’s Schwarzschild radius.

3.2.2. The Sgr A* Schwarzschild Radius

Once the Sgr A*’s mass is determined, its Schwarzschild radius can be computed using this equation:

\( {r_{s}}=\frac{2G{M_{Sgr A*}}}{{c^{2}}} \) (8)

Substituting the Sgr A*’s mass ( \( {M_{Sgr A*}} \) = 4.1 × 10⁶ M_⊙ = 8.2 × 10³⁶ kg) into this equation yields:

\( {r_{s}}=\frac{2×6.67×{10^{-11}}×8.2×{10^{36}}}{{(3×{10^{8}})^{2}}} \) (9)

This leads to a Schwarzschild radius of:

\( {r_{s}}={1.22×10^{10}} \)

The boundary of the event horizon is characterized by the Schwarzschild radius. Within this surface, neither matter nor light can escape. A spacetime diagram illustrates the light cones both within and beyond the event horizon of Sgr A* (refer to Figure 5). As matter approaches the event horizon, the black hole's powerful gravitational field causes the light cones to bend inward. Its result is trapping light and matter within the horizon.

Figure 5: Spacetime diagram showing light cones outside and inside the event horizon surrounding Sgr A* [28].

While these calculations are useful for viewing Sgr A* as a Schwarzschild black hole and can be pedagogically very illustrative, they are based on assumptions of ideal conditions (e.g., no spin or charge). Observationally, it seems likely that Sgr A* actually has quite a lot of spin, so the Kerr model is somewhat more appropriate.

3.3. The Potential of Sgr A* as a Kerr Black Hole

The astrophysical evidence indicates that Sgr A* is probably not a Schwarzschild black hole. If spin can be evidenced through detections of gravitational waves or outflows, then maybe Sgr A* would belong to the family of spinning Kerr black holes. Angular momentum is a property of Kerr black holes, which makes them entirely dependent on their rotation status, drastically changing their behavior and configuration by, for example, establishing an ergosphere and the frame-dragging effect.

3.3.1. Evidence of Spin from Gravitational Wave Detection

Kerr model for Sgr A* is one of the cases receiving stronger support from evidence, and this proves the detections of gravitational waves (GWs). An event reported by Vázquez-Aceves et al., the gravitational waves coming from a Brown dwarf inspiraling into the massive black hole Sgr A* [29]. The extreme mass-ratio inspirals (EMRIs) system will provide an accurate method for determining the mass and spin of Sgr A* [30].

The spin parameter of Sgr A* had been estimated from GWs data to lie within the interval 0.1–0.9, as summarized in Table 2. We reiterate that the range of spin values indicates that Sgr A* behaves significantly different from a stationary black hole of Schwarzschild. The observation of gravitational waves, particularly through EMRIs, allows for the inference of Sgr A*'s angular momentum. The spin parameter is crucial in determining whether Sgr A* is classified as a Kerr black hole.

Table 2: Data showing the range of possible spin parameters for Sgr A* based on gravitational wave detections [29].

3.3.2. Deduction of Spin from GWs

Gravitational waves, by their very nature, are spatial disturbances caused through the rapid movement of large celestial bodies, like black holes or neutron stars. The GWs detected from the matter around Sgr A* imply that the black hole is spinning. The formula derived from the Kerr solution for spinning black holes allows for the determination of energy radiation within these waves. Consequently, the rotational energy of a spinning black hole can be articulated as:

\( {E_{spin}}=\frac{1}{2}Ω_{H}^{2}If_{s}^{2} \) (10)

where \( {Ω_{H}} \) and \( I \) are the angular velocity and moment of inertia, respectively. As illustrated by the waveform breakdown related to the rotating black hole (refer to Figure 6), a portion of the hole's energy stemming from its spin is being radiated away via time-dependent gravitational waves, further facilitating the process of spin-down for the black hole [31].

These gravitational wave signals themselves, together with what we infer from them based on observation, offer compelling arguments indicating that Sgr A* is truly a Kerr black hole exhibiting significant spin.

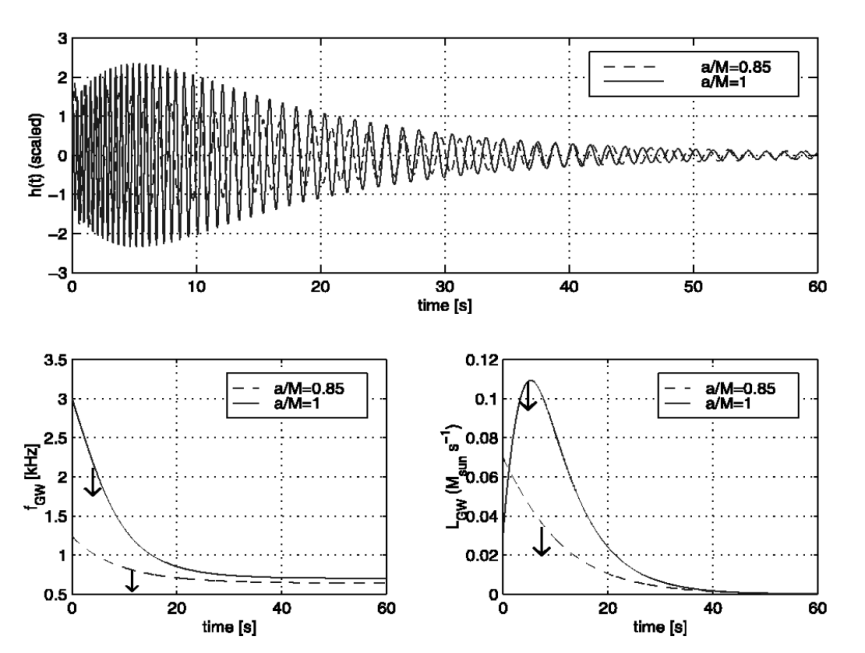
Figure 6: Gravitational waveforms generated by a black hole of Kerr influenced by surrounding matter [31].

3.4. Comparison and Evaluation

The answers of Schwarzschild and Kerr to equations of Einstein’s field represent two black hole models, each with different sets of assumptions and consequent implications. Of the Schwarzschild models, the nonrotation, uncharged hole is just the simplest. While useful pedagogically and quite adequate for many idealized situations, it is becoming more and more evident that it falls far short of explaining fully the observed Sgr A*’s properties.

The Schwarzschild model assumes no angular momentum. This is a significant limitation because in astrophysical reality, it is anticipated that the majority of black holes possess a certain degree of spin. In truth, nearly all black holes are left-over products resulting from the large stars’ gravitational collapse, and in such process, spin is an invariable quantity of gravitational attraction, provided that the ideal initial condition should be absolutely symmetric and without rotation—which is actually an extremely rare case in the universe from statistical viewpoints. Considering that black hole formation processes are highly dynamical and often involve violent events for supermassive black holes, it is quite expected that Sgr A* would show considerable rotational properties.

On the other hand, the Kerr solution that characterizes a spinning black hole provides a more realistic framework in studying astrophysical black holes. The Kerr metric incorporates angular momentum and is distinguished by the existence of an ergosphere, a zone beyond the event horizon where spacetime is pulled along by the rotating black hole. Such effect of frame pulling is one of the principal discriminating features between Kerr black holes and others; and it has profound consequences for how matter behaves in the vicinity of a black hole along with for the generation of phenomena like relativistic jets.

4. Conclusion

This study has probed the properties of Sgr A* and assessed whether it acts more like a Kerr or Schwarzschild black hole. It shows that the properties of Sgr A* are best explained if we assume it to be a Kerr black hole, which is supported by evidence from gravitational wave detections and dual collimated outflows. The large angular momentum gives Sgr A* a physical motivation to be as a black hole of Kerr.

Such implications for the future research on black holes. If indeed Sgr A* is a Kerr black hole, then this may be a near confirmation that many supermassive black holes located in distant galaxies are also endowed with significant spins, possibly affecting interactions with the surroundings. Essential to model improvement in particular is also the spin property of such black holes as Sgr A* in particular.

The astrophysical interest of this study is wider. Having obtained that Sgr A* imitates known rotational features, we can be more certain in our expectations related to the influence of supermassive black holes on the galaxies they inhabit. Processes that can be driven in a galactic core relate to spins of black holes, including jet- and outflow-formation mechanisms, and they eventually contribute to the fine-tuning of regimes for star formation and matter distribution within galaxies. The better we know about the spin of black holes, the more our notions about galaxy formation and evolution will advance along with our models.

In conclusion, while Schwarzschild modeling of Sgr A* may be a useful simplification, increasingly the evidence is suggesting that it is a rotating Kerr black hole. Further progress in observational technology will lead to better refinement of these findings and further consideration regarding the influence of black holes.