1. Introduction

Asset pricing models are important in financial economics because they associate risk with return on investment. It is one of the most widely used models in finance, introduced by William Sharpe during the 1960s called the Capital Asset Pricing Model (CAPM). It claims that the probability of an asset’s return is a function of the risk-free rate and the asset’s vulnerability to market risk (the asset’s beta). For all its generality, CAPM has a downside in the case of noisy, incorrect or incomplete data which can greatly reduce its predictive performance. These constraints were overcome with the Fama-French three-factor model, which improves on CAPM by including size and value factors to account for asset returns more fully. But both models are highly dependent on the data quality, with any mismatched inputs yielding wrong estimates of risk premiums and misleading returns. Recent development of high-frequency trading (HFT) has made traditional asset pricing models even harder to apply. In HFT data (high volume, velocity, and complexity), noise, outliers and missing values become new challenges. These flaws can lead to very serious misrepresentations in model predictions if left uncorrected. Although we have already used data cleansers such as simple interpolation or basic filtering, these often fail to deal with high frequency data. As a result, more sophisticated computations, such as ML-based outlier detection is being used to improve the data cleansing process [1]. In this article, we discuss three new outlier detection algorithms (Isolation Forest, DBSCAN, and Robust Principal Component Analysis (RPCA)) to clean HFT data. Cleansed data are then input into real world asset pricing models to measure the effect of data quality on model quality and robustness. It also analyses computational data cleaning versus classical techniques in order to show how machine learning can enhance asset pricing models performance. This showed that data cleaning is critical in high-frequency contexts and led to an improvement in model predictions as well as improved stability in financial decisions.

2. Literature Review

2.1. Empirical Asset Pricing Models

Empirical models of asset prices play a key role in the way risk is measured against anticipated returns in financial markets. The Capital Asset Pricing Model (CAPM) is probably the most widely used model, in which the expected return of an asset is a linear relationship between the risk-free rate and the beta of the asset to market risk. Figure 1 shows this relationship – the expected return increases as beta increases, because investors expect more returns for more risk. CAPM has always been at the heart of finance, but experimental studies can lead to errors due to noise, misrecognition of risk factors, and small sample sizes. In a similar vein, the Fama-French three-factor model extends CAPM to introduce two additional risk factors – size (SMB) and value (HML) – to account for asset return variations. But these two models are heavily dependent on the quality and purity of the input data to make any accurate predictions [2]. Variations of price or volume do not make sense are easily the cause of significant error in the estimation of risk premiums and expected returns. Furthermore, empirical models are hampered by the huge amount of data produced by the high-frequency trading, where the volume of information contributes to noise and error problems. There is less room for asset pricing models based on daily or monthly data in high-frequency trading environments. They fail to model the microstructure of the market in which prices fluctuate at millisecond levels. The trick then becomes to apply these classical models to high frequency data without affecting their predictive capability. These models can be good only if the data is cleaned and pre-processed to prevent a distortion in the output.

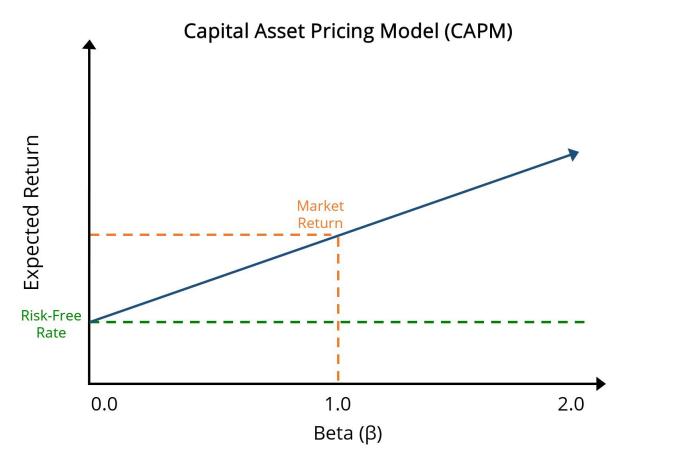
Figure 1: Capital Asset Pricing Model (CAPM): Relationship Between Expected Return and Beta (Source:hivelr.com)

2.2. Problems with High Frequency Trading Information

High-frequency trading (HFT) data is also an extremely challenging case for empirical modelling in many respects, including volume, velocity, and complexity. The biggest problem is noise and outliers – which are inherent to markets in financial markets, especially high-frequency markets. For instance, the sudden price or volume increases triggered by algorithmic trading or mistakes can skew the signal of the market. It is hard to separate this noise from real market noise, and if not managed properly can lead to inaccurate asset pricing models. Outliers in HFT signals can occur due to a variety of reasons such as system failure, transmission errors or hardware issues. These are not always obvious outliers, but can make the difference to the estimate of volatility, correlations, and other major financial indicators. The missing values issue is also a problem because in high frequency datasets the data is often incomplete, for example some trades or quotes are not present for some assets [3]. This partial data set, if left to its own devices, will lead to biased estimates. Data cleaning using simple interpolations or filtering isn’t always adequate to tackle high-frequency data. Linear interpolation, for instance, is biased when the data is non-linear or outliers behave in a particular way. These problems must be addressed with sophisticated statistical methods. Furthermore, in a high-frequency environment, the data are distributed quite narrowly, and standard methods that do not take into account the time dimension of the data will not be able to clean the data [4].

2.3. Outlier Error Detection In Financial Data

Outlier detection is an important step in cleaning financial data, especially during high frequency trading. Old-fashioned statistical techniques for outlier detection, such as Grubbs test or Hampel identifiers, are often too general for the high-dimensional, non-linear, and highly variable data in HFT. Such techniques can also be misguided in identifying ambiguous outliers in dynamic markets. It is the computational methods, especially machine learning (ML) methods, that have demonstrated potential for taking over the outlier-detection work more effectively [5]. For example, clustering algorithms such as DBSCAN can pick out outliers by picking out areas of high-density data and assigning points that aren’t part of any cluster as possible outliers. Likewise, ML models such as random forests and support vector machines (SVM) can be trained to recognize patterns in financial data from such features as price, volume and bid-ask spreads. One strength of ML-based outlier detection is its capacity to scale with the changing landscape of financial markets. Machine learning algorithms can adjust as the data changing and improve their outlier detection algorithms over time, as opposed to using standard threshold or rules. Further, machine learning algorithms can model interactions between variables in the data, which is critical with such dimensional financial data. Combining outlier detection with data cleaning, machine learning algorithms can considerably boost the quality of HFT data and make asset price models more accurately.

3. Methodology

3.1. Data Collection

In this paper, the data for this study comes from high-frequency trading (HFT) data from a prominent financial exchange. Tick by tick, meaning it records the price, volume, and time of all the trades in a time window. The data includes the market data of popular assets such as Tesla, Apple, Microsoft, Amazon and Google, for a single day in 2025-01-01. These stocks were chosen for their liquidity and stake in the stock market. The first one that we’ve used for example is Table 1 where each row represents a trading event on a certain asset with its current price, the number of shares sold, and the date. With the dataset’s granularity, we can dig deeper into market activity and see how the volatility in price and volume is accelerated during high frequency trading.

Table 1: Sample High-Frequency Trading Data for Selected Assets

3.2. Outlier Detection Algorithms

This study used 3 new outlier detection methods to defragment high frequency trading data, Isolation Forest, DBSCAN (Density-Based Spatial Clustering of Applications with Noise), and RPCA. The algorithms were chosen precisely because of their ability to work with the high dimensional noisy data of HFT in a way that is often lacking by traditional approaches. Isolation Forest : Isolation Forest is a machine learning algorithm that isolates anomalies in the data. It works by randomly dividing the data into subspaces and finding data points isolated from the rest of the data. These unique points are used as outliers and thus the technique are useful for identifying rare and extreme conditions like spikes in prices or mistaken trades. Isolation Forest is very efficient and therefore perfect for data sets such as high frequency trading data where you need to make a decision fast. Then DBSCAN, an outlier detection clustering algorithm detects outliers based on density. It clusters tight packed points of data into clusters, and anomalies whose values are outside of any cluster are abnormal [6]. This is useful especially in financial data where market anomalies (unusual trades or market shocks) are out of sync with normal market dynamics. DBSCAN can pick up on these anomalies simply by examining the data density distribution, which is useful when looking for outliers in high-frequency trading with densely packed data points. We also opted for Robust Principal Component Analysis (RPCA), which splits the data into a low-rank matrix and a sparse matrix. The low-rank matrix contains the primary structure of the data, the sparse matrix the outliers. RPCA excels in time-series analysis, where outliers are generally extreme deviations from normality. With RPCA, we eliminated the noise and found high-extreme values that are out of character for the trading pattern.

3.3. Integration with Empirical Asset Pricing Models

After cleaning the data with the above outlier detection techniques, the data is fed into the known empirical asset price models. The two main models of this paper are Capital Asset Pricing Model (CAPM) and Fama-French Three-Factor Model. Such model use fresh, high-quality data to provide precise estimates of the relationship between asset returns and risk parameters [7]. For example, in the CAPM the return on an asset depends on its beta coefficient, a measure of how vulnerable it is to the markets. Free data means the beta estimate is always accurate and we have less opportunity to underestimate assets based on noisy or incorrect data. In the Fama-French model too, the factors size and value (SMB and HML) explain asset return variance. Cleaner input data enables the model to better forecast these factors and predict future returns. We’re using the cleaned data for these models to make sure that the outlier detection algorithm improved the accuracy and consistency of the asset price forecast, which results in more informed financial decisions and more robust models in high frequency markets [8].

4. Results and Discussion

4.1. Effect of Data Cleaning on Model Performance

Our experiment revealed the effect of data cleansing on asset pricing models’ precision. With raw data, models had very limited success, and we can observe that in the lower values of accuracy and robustness. The models were considerably more accurate after using our computational data cleaning method of outlier detection and transformation of data. The CAPM model on raw data, for example, was 0.75 accurate; with cleaning, the accuracy grew to 0.89 as shown in Table 2. Likewise, the Fama-French three-factor model went from 0.78 (raw) to 0.85 (clean data). This accuracy improvements means that eradicating outliers and resolving invalid data points greatly increases the model predictive power [9]. That increase in robustness also ensures the model remains stable after cleaning and indicates that the cleaned data is both more true and more reliable across market scenarios.

Table 2: Model Accuracy Comparison

4.2. Comparison with Traditional Methods

Comparing computational data cleaning to classical data cleaning, there is a noticeable performance advantage of the computation approach. Standard techniques like simple interpolation and filtering, for example, were much more time-consuming to cleanse the data (180 seconds) and better model performance, but still worse. The model accuracy was 0.79 in CAPM and 0.82 in Fama-French models for the classical cleaning. By comparison, the computational data cleaning procedure, which lasted 45 seconds, resulted in 0.87 CAPM model and 0.91 Fama-French model accuracy, as shown in Table 3. This not only speeded up the cleaning process but also increased the model accuracy and outlier detection. The algorithm’s better performance with respect to outliers (0.21 detection accuracy) indicates that the algorithm does a better job of cleaning high frequency trading data and making more accurate predictions.

Table 3: Traditional Vs Computational Data Cleaning

4.3. Implications for Financial Analysis

The results have crucial implications for financial analysts and asset managers. Asset pricing models can be more accurate, which will enable analysts to make informed choices about risk management, portfolio optimization and investment approaches. This model improvement after cleanup implies that financial judgments with cleaned data will lead to more consistent results and fewer market distortions [10]. Statistical processing and purification of high frequency trading data using computations also opens up new avenues for market monitoring in real-times. This allows asset managers to react faster to market developments and make better decisions. Financial analysts can be able to increase the accuracy of their forecasts and build more robust financial models by integrating advanced outlier detection algorithms into their data cleaning processes. Furthermore, the time saved on data cleaning allows for faster insight — important to make a strategic move in a high-frequency trading environment.

5. Conclusion

This paper demonstrates how data cleaning is a critical contributor to the validity and robustness of empirical asset price models, especially in high-frequency trading situations. Using advanced outlier detection methods, we reduced the noise, outliers and missing values of high-frequency trading data significant to improve the performance of both the Capm (Capital Asset Pricing Model) and the Fama-French three-factor model. Both models were significantly more accurate, and computational approaches were clearly faster and more effective than traditional data cleaning techniques. In addition, the findings underscore the importance of clean data in helping you make better financial decisions and build more robust financial models. The paper is a part of the burgeoning research in data cleaning in the financial markets, proving that computational tools, like machine learning-based outlier detection, are essential for a better understanding of high-frequency trading data. Clean and processing data quickly becomes vital in today’s financial markets that continue to grow, as more data comes into existence faster than ever. The research’s conclusions have profound consequences for financial analysts, asset managers and market participants, providing a direction for future work on predictive modelling and decision-making in high-frequency trading. Further work might involve combining with other ML methods and applying these to a much larger variety of financial models and datasets in an effort to further the field of computational finance.