1. Introduction

The brachistochrone problem, a classic optimization problem, originates from the exploration of the shortest path in time for an object to fall freely from one point to another under the effect of gravity. This problem holds significant importance in physics and has been widely applied in fields such as mathematics and engineering [1]. Recent studies have explored the brachistochrone problem using tools like variational methods and Euler-Lagrange equations, especially in various physical contexts. However, gaps remain in optimizing the fastest path in complex media and real-time optimization in dynamic systems [2]. This paper explores the basic principles of the brachistochrone problem and its practical applications, especially in engineering. In addition, it simplifies traditional answers to the problem by examining variational and parametric methods, demonstrating how these approaches can optimize path design because of their ability to optimize path design. The paper also examines how brachistochrone theory applies to different media, addressing optimization issues encountered in engineering. Therefore, this study aims to investigate how to construct the most efficient path for descent by using this theory and to simplify the process of solving equations by utilizing parametric techniques. Through the presentation of these methods, it may provide valuable insights for future dynamic optimization challenges.

2. The Basic Principle and Solution Methods of the Brachistochrone Problem

2.1. Problem Definition and Physical Background

The brachistochrone problem concerns determining a curve under the influence of gravity along which a particle travels from an initial point \( A(0,0) \) to point \( B({x_{f}},{y_{f}}) \) , as shown in Figure 1. Here, points A and B are not on the same horizontal plane, and and the curve connecting these two points is the one to be determined. In the context of physics, the problem assumes that the particle starts at point A with an initial velocity of zero and moves freely along the curve under the influence of gravity. Notably, this problem depends not only on the geometric shape of the curve but also on the effects of gravitational acceleration. In this context, minimizing the total duration of descent, the major optimization variable, is the primary goal. Theoretically, the total time can be computed by integrating the curve’s arc length with respect to the particle’s velocity. However, achieving time minimization requires constructing an appropriate optimization model. Specifically, this problem is typically addressed using the calculus of variations to identify the curve that satisfies the optimality conditions [3].

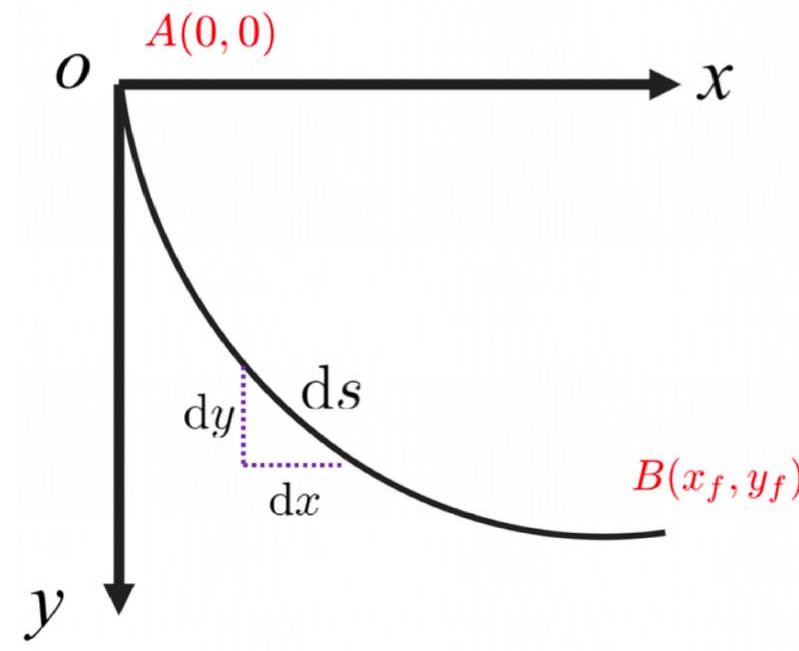
Figure 1: Differential Diagram of the Brachistochrone Path

2.2. Objective Function and Variational Method

To solve the brachistochrone problem, the first step is to define the objective function. The velocity v of the falling object is determined by the relationship between gravitational acceleration g and the vertical position y [4]. If the velocity of the object at position y is given by \( v=\sqrt[]{2gy} \) , then the time element \( dt \) can be expressed in terms of the arc length \( ds \) and the velocity v as:

\( dt=\frac{ds}{v}=\frac{ds}{\sqrt[]{2gy}} \) (1)

In this case, the total time t is the integral of the time required to travel along the path from point A to point B. The goal is to minimize this total time. To achieve this, the variational method can be applied, solving the Euler-Lagrange equation to obtain the path that minimizes the time. The Euler-Lagrange equation is a commonly used tool for solving optimization problems, and in this problem, it helps derive the specific expression for the Brachistochrone. It is important to note that the objective function is dependent on the gravitational acceleration g as well as the slope of the route, and the Euler-Lagrange equation indicates the relationship that exists between these two parameters.

2.3. Model Simplification through Parameterization

The application of the Euler-Lagrange equation theoretically leads to the derivation of the equation for the brachistocentric curve. However, the equation involves complex second-order derivatives, which makes the process of finding a solution extremely challenging. Thus, to simplify the solution, it is common to introduce an appropriate parameterization to make the problem more intuitive. In this case, a parameter a is introduced (e.g., let \( y \prime =cot{a} \) ), hence transforming the equation and simplifying the solution process. This technique not only simplifies the computation but also makes the solution more clearly defined. Through this parameterization, a clear expression for the path can be obtained and further solved using standard integration methods. The parameterization approach is crucial in practical problem-solving as it effectively reduces the complexity of the equations and transforms the problem into a more intuitive form, making both analysis and computation more straightforward [5].

2.4. Final Results and Physical Significance

The parametric equations of the Brachistochrone issue can be obtained by applying the procedures described above. One way to describe the end product is as:

\( \begin{cases} \begin{array}{c} x={C_{1}}(2a-sin{2a)+{C_{2}}} \\ y=\frac{{C_{1}}}{2g}(1-cos{2a) } \end{array} \end{cases} \) (2)

where constants \( {C_{1}} \) and \( {C_{2}} \) are determined by the boundary conditions. These equations allow us to clearly describe the specific form of the shortest time path from point A to point B.

The solution to the Brachistochrone problem exposes the natural trajectory of an object when it is subjected to the impact of gravity. This is the reason why this conclusion is significant from a physical standpoint. Along this curve, the object can fall from the starting point to the endpoint in the shortest time. This not only provides a classic solution to an optimization problem in physics but also offers valuable insight into the application of variational methods [5].

3. Innovative Approaches and Numerical Solutions

The problem of particle motion in an inhomogeneous medium is broken down into two distinct approaches: the analogy method and the variational method. Both of these approaches are presented here. It is possible to discover the motion laws of particles in a variety of physical situations by doing a quick analysis of these methods. Furthermore, useful mathematical models and solutions for difficult problems are presented.

3.1. Analogy Method

The Brachistochrone problem can be solved using the analogy approach, which gives a physical perception of the particle’s trajectory. And a particle’s journey in a non-uniform media can be determined using Snell’s law by drawing a comparison to the path of light in an inhomogeneous medium. However, when the problem has complicated limitations, analogy approach theoretical analysis typically fails to produce precise numerical answers. Thus, combining numerical methods to solve the Brachistochrone problem under complex constraints becomes crucial. For instance, traditional analytical methods often fail to solve problems with inhomogeneous gravitational fields, uneven boundaries, or other complex physical situations. In such cases, numerical methods can effectively handle these complex constraints, providing specific path calculations and optimizations. The optimal particle path is obtained by converting complex restrictions into mathematical models using numerical solutions. And common numerical approaches include variational methods with numerical optimization, finite difference methods, and Monte Carlo simulations. These methods can not only handle complex physical conditions but perform precise optimizations in computations to obtain the shortest time path that satisfies the constraints. Combining these numerical methods with the analogy method improves knowledge of the particle’s route in non-uniform medium and solves the Brachistochrone problem under complex limitations in actual applications.

3.2. Variational Method

The variational method describes particle motion in inhomogeneous media based on the law of energy conservation. When assuming that the particle moves in a gravitational field with no other non-conservative forces acting, the law of energy conservation provides a strong constraint on the system. The total energy of the particle comprises potential and kinetic energy, with the initial total energy being solely potential when the particle begins from rest. As the particle traverses the medium, its kinetic energy is observed to increase. The particle’s velocity expression can be derived through the principle of energy conservation. Due to medium resistance, particle velocity fluctuates in inhomogeneous media. The resistance term is added to the dynamical equation if the resistance is proportional to velocity and has a coefficient of k. The conservation of energy and the drag yield the particle’s motion equation. First, the law of conservation of energy is considered. At height \( {y_{0}} \) , the particle is at rest, and the total energy is \( mg{y_{0}} \) . At height \( y \) , the kinetic energy \( K=\frac{1}{2}m{v^{2}} \) , and the velocity expression can be derived from energy conservation:

\( v=\sqrt[]{2g({y_{0}}-y)} \) (3)

Resistance changes velocity v in an inhomogeneous material. Dynamic equation for particle if resistance is proportional to velocity and k is a resistance coefficient:

\( ma=mg-kv \) (4)

Combining with the kinematic formula \( v=v(y) \) (where velocity is a function of height y), this equation transforms into the differential equation:

\( (\frac{mv}{mg}-kv)dv=-dy \) (5)

By integrating this differential equation, the relationship between velocity and position can be derived. Let \( p=mg-kv \) , then the equation becomes:

\( -\frac{k}{m}\frac{mg}{p}dp=dy \) (6)

After integration, the particle’s motion expression is obtained:

\( \frac{g}{k}ln{|p|}+\frac{mg}{k}ln{|p|}=y+C \) (7)

where C is the integration constant. Substituting \( p=mg-kv \) into the equation, the velocity expression for the particle in the inhomogeneous medium is obtained.

The variational method provides a theoretical framework for the Brachistochrone problem, but it needs to be solved with the help of numerical methods under complex constraints (such as irregular boundaries and inhomogeneous media). To compute the shortest path, the variational problem can be discretized into a numerical equation using finite difference, finite element, and other methods. It can handle inhomogeneous gravitational fields and variable resistance with numerical optimization (gradient descent, Newton's method) and determine the optimal path through iterative optimization. Combining the variational and numerical methods overcomes the analytical method's limitations and solves complex constraint problems.

4. Practical Applications of the Brachistochrone Problem

4.1. The Deceleration Problems in Heterogeneous Media and Engineering Applications

The Brachistochrone problem optimizes heterogeneous media deceleration processes, thus making it useful in engineering. In various engineering practices, deceleration problems in heterogeneous media often require finding the optimal path between different materials and media. The theory of the fastest descent provides the theoretical foundation for this process. It is feasible to efficiently slow down energy transfer or speed propagation through optimization design, which lessens the influence on the environment. For example, in open-pit mining, optimal blasting technology may effectively regulate blasting vibrations and mitigate environmental damage by accurate design of blasting timing and explosive quantity. The use of inter-hole non-electric detonator millisecond delay blasting network design can significantly reduce the cumulative vibration effect, thereby protecting the surrounding buildings and facilities [6]. In addition, by optimizing the design and application of flow mitigation structures, effective control of high velocity flood discharge can be achieved, ensuring project safety and environmental friendliness. This optimization approach has shown practicality and reliability in a variety of engineering scenarios, providing a systematic solution to the problem of deceleration in complex media.

4.2. The Brachistochrone Problem in Non-Uniform Sampling and Signal Reconstruction

The brachistocentre problem provides theoretical support for optimizing data sampling and signal reconstruction, especially in the fields of non-processing signals, non-uniform sampling and signal reconstruction. In signal processing, uniform sampling requires optimizing the sampling rate and data volume while ensuring signal quality. In this process, the brachistocentre theory provides a systematic optimization framework. By use of reconstruction techniques and sampling point design, it is feasible to reduce waveform data while preserving signal reconstruction integrity. In picture and video signal processing, non-uniform deceleration sampling techniques can markedly enhance storage and transmission efficiency, particularly in extensive data processing contexts. And the optimized sampling method based on the brachistocentre theory realizes efficient sampling and reconstruction of image signals via block partitioning and adaptive sampling frequency selection [7]. This method can not only significantly reduce the amount of data, but improve sampling efficiency, while ensuring that the reconstruction quality meets actual needs. It is widely used in the rapid processing of static images and video signals. In addition, there is a lot of room for growth and application because comparable optimization methods have already been expanded and used to other rapid storage and data compression issues. Incorporating the brachistocentre theory into data processing offers a fresh perspective on optimizing non-uniform sampling and signal reconstruction.

4.3. The Deceleration and Compression Optimization Techniques in Transportation and Communication Systems

The brachistocentre problem-derived optimization methods in transportation and communication systems can substantially boost system efficiency, reduce resource waste, and optimize the design process. These systems usually deal with complex dynamic problems such as vehicle air resistance, vehicle deceleration design, and antenna compression optimization [8]. The brachistocentre theory helps determine the best deceleration or compression path for these systems. This not only enhances system performance through rational design, but also reduces energy consumption and improves energy efficiency. For instance, the aerodynamic design of high-speed trains can be enhanced by optimizing the windscreen design and incorporating bio-inspired channels to effectively reduce air resistance, thus enhancing transportation efficiency. In communication systems, improving antenna designs reduces size and improves performance. In high-speed train design, numerical simulations based on the SST k-ω model have shown that optimizing the windscreen and aerodynamic shape can reduce air resistance by approximately 8.17%, effectively boosting energy utilization efficiency [9]. The non-uniform compressed antenna design controls medium distribution and compresses the antenna structure to improve gain and beamforming, providing novel antenna design ideas. For example, to reduce greenhouse gas emissions from ships, research on speed optimization and urban planning has also made significant progress. The transportation sector encounters analogous issues with speed optimization and structural design. Research shows that speed optimization, shown by gasoline organization tax, and structural adjustment, such as enforced speed limits, possess distinct advantages and disadvantages. The International Maritime Organization (IMO) is discussing speed optimization and emission reduction as potential short-term measures to reduce greenhouse gas emissions from ships [10].

5. Conclusion

This paper presents a thorough examination of unique research methods and accomplishments related to the brachistochrone problem, including solutions in non-uniform media and under various limitations, as well as their applications. Despite standard analytical solutions offering theoretical support for the brachistochrone problem, resolving it in intricate contexts and under various restrictions continues to pose a considerable difficulty. In recent years, numerical methods based on optimization algorithms have made significant progress, particularly in dynamic environments, non-uniform media, and multi-objective optimization, demonstrating great potential for application. In engineering practice, the brachistochrone problem has been widely applied in various fields such as open-pit mining, signal processing, and traffic systems, providing effective optimization solutions. Future research should focus more on solution methods in complex physical environments and engineering applications, further improving the efficiency and accuracy of algorithms as well as promoting the development of related technologies.