1. Introduction

Black holes are among the most fascinating and extreme objects in the universe, defined by their mass and spin. The spin of a black hole is commonly described by a dimensionless parameter, a* = cJ / (GM^2), which is a function of both the black hole's angular momentum (J) and its mass (M). [3] This parameter greatly affects the dynamics of the accretion disk, relativistic effects in the region near the event horizon, and the generation of high-energy emissions, making it a crucial parameter in the field and theory of black hole physics. [4]

Two principal spectroscopic techniques are used to determine the spin of a black hole: the continuum-fitting method and the relativistic reflection method. [1] The latter is a strong approach that uses the distorted features of the X-ray spectrum from the accretion disk. Both of these are influenced by the system's geometry and the location of the Innermost Stable Circular Orbit (ISCO). The ISCO is a region governed by the black hole's spin and thus provides information about the black hole's spin. [5]

This study investigates black hole spins using the relativistic reflection method. Section 1 focuses on the relativistic reflection method, which analyses distorted X-ray spectra, in particular the broadened Fe Kα line, and highlights black hole spin as a critical parameter influencing accretion disk dynamics and high-energy emission. Section 2 explains the sensitivity of the method to the innermost stable circular orbit (ISCO) and how it affects spectral features such as gravitational redshift and light bending. Section 3 shows that advanced models such as RELXILL improve the accuracy of spin measurements by incorporating ionisation and relativistic blurring. Section 4 presents spin results from 33 black holes, including 14 stellar-mass black holes and, 19 supermassive black holes. Section 5 shows the discussion, confirming the reliability of the method. Section 6 shows the conclusion.

2. The theory of relativistic reflection method

The key benefit of the relativistic reflection method is its capacity to explore the innermost regions of the accretion disk, where relativistic effects are most prominent. The sensitivity of this method to the ISCO makes it an especially effective means of measuring black hole spin. [6] The ISCO, which is dependent on the spin of the black hole, represents the inner boundary of the accretion disk. In the case of rapidly spinning black holes, the innermost stable circular orbit is located in closer proximity to the event horizon, which gives rise to more discernible relativistic effects. The shape and extent of reflection features, particularly the broadening of the iron K-alpha line, are directly associated with the spin parameter, making the relativistic reflection method an effective technique for investigating the angular momentum of black holes. [7]

3. Reflection model development

Developing reflection models has greatly improved the accuracy of measuring black hole spin. Early models such as Diskline and LAOR were fundamental, but lacked precision due to their simplistic assumptions and their inability to fully account for relativistic effects, ionisation of the disc, and the angular dependence. [4] Advanced models such as reflionx and xillver introduced detailed atomic data and ionisation effects. [8] These models greatly improved the accuracy of reflection spectrum analysis. Reflionx provided angle-averaged solutions, while xillver extended this by including angle-dependent solutions that capture emission variations caused by relativistic light bending and disk geometry. The RELXILL model developed by García, Dauser and co-workers represents a major advance. It combines the strengths of reflionx and xillver with relativistic blurring. It self-consistently integrates microphysics, such as atomic interactions and ionisation, with macrophysics, including Doppler shifts and light bending, to analyse reflection features such as the iron line and the Compton hump with high precision. [8] RELXILL also offers versatile configurations, including RELXILLD for high-density discs, RELXILL_LP for lamppost geometry and RELXILL_NK for testing general relativity deviations. By correcting for biases in previous models, RELXILL improves the accuracy of parameters such as black hole spin and tilt angle. Its use with high quality data from XMM-Newton and NuSTAR has produced consistent and precise results, making RELXILL an important tool for studying black hole environments and testing strong field gravity. [4]

4. Spin results distribution of black holes

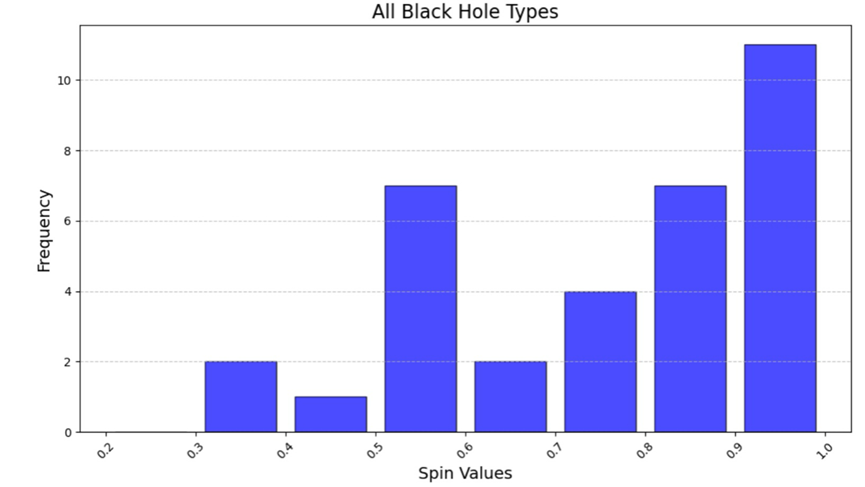
Figure 1: The figure shows the frequency distribution of spin values for 33 different black holes, including 14 stellar-mass black holes and 19 supermassive black holes. The spin data is from [1].

Figure 1 shows the spin distribution for 33 black holes, including 14 stellar-mass black holes and 19 supermassive black holes. The spin values used in Figure 1 were taken from Tables 1 and 2 of [1], which provide spin measurements for black holes. Where a spin value was presented as a range (e.g. a minimum and a maximum), the median of that range was chosen for consistency. In cases where the spin was reported as greater than a certain value (e.g. >0.5), this paper has directly adopted the stated minimum value, e.g. quoting 0.5 for a spin listed as greater than 0.5.

This will ensure that all spin values in the figure are presented in a consistent and comparable format, thus allowing accurate interpretation and analysis of black hole spin distributions. Figure 1 reveals a strong prevalence of high-spin systems (≥0.8), low-spin black holes (<0.4) are rare.

In cases where the spin was reported as greater than a certain value (e.g. >0.5), this paper has directly adopted the stated minimum value, e.g. quoting 0.5 for a spin listed as greater than 0.5. This will ensure that all spin values in the figure are presented in a consistent and comparable format, thus allowing accurate interpretation and analysis of black hole spin distributions. [9] Figure 1 reveals a strong prevalence of high-spin systems (≥0.8), low-spin black holes (<0.4) are rare.

Figure 2: The figure shows the frequency distribution of spin values specifically for stellar black holes, as extracted from Figure 1.

Figure 2 shows the spin distribution of stellar-mass black holes. It reveals a strong dominance of high-spin (≥0.8) systems. [1] This dominance is driven by efficient binary accretion processes. The accretion disk is oriented towards the spin axis of the black hole, due to the transfer of angular momentum from the companion star. Over time, this coherent accretion leads to rapid rotation, especially in systems with stable, long-term accretion. [2]

Moderate spin systems (0.4-0.6) are less common in the distribution, reflecting their association with disordered or chaotic accretion histories. Such systems may experience irregular angular momentum transfer, either due to misalignment of the binary components or to short-lived accretion phases. This limits their ability to sustain high spin rates. [7]

Figure 3: The figure shows the frequency distribution of the spin values for supermassive black holes, which was derived from the data shown in Figure 1.

Figure 3 shows the spin distribution of supermassive black holes (SMBHs), with the majority of them having high spins (≥0.8). This is mainly due to two factors: prolonged disk accretion and aligned mergers. In galaxies without recent mergers, SMBHs acquire high spins due to prolonged and steady accreting gas. The gas flows into the black hole in the same direction for long periods of time. This adds angular momentum and accelerates the black hole's spin. Research such as the Horizon AGN simulation supports this. It shows that SMBHs tend to spin faster in stable environments without collisions. [10] Aligned mergers also play a role in increasing spin. The spin of the new black hole is increased when galaxies or black holes merge, and their angular momentum aligns with the spin axis of the black hole. This alignment maintains or enhances spin after the merger. [11]

Medium-spin (0.4-0.6) and low-spin (<0.4) SMBHs are comparatively rare, being associated with inefficient accretion processes or chaotic growth histories. Spin evolution in these systems is limited by inconsistent angular momentum transfer, misaligned mergers or short-lived accretion episodes. The scarcity of such SMBHs highlights the importance of sustained, coherent accretion and aligned mergers in the formation of high-spin SMBHs. [7]

5. Discussion

The spin distributions in Figures 1, 2 and 3 show consistent patterns across the black hole populations, highlighting a strong dominance of high-spin (≥0.8) systems in both stellar-mass black holes and supermassive black holes (SMBHs). This indicates the efficiency of sustained accretion processes and coherent angular momentum transfer. For stellar-mass black holes (Figure 2), spin is primarily driven by binary accretion, where material from a companion star is aligned with the spin axis of the black hole. For SMBHs (Figure 3), high spin result from prolonged disk accretion or aligned mergers in active galactic nuclei, where large-scale angular momentum transfer favours rapid rotation. Medium- and low-spin systems are less common, reflecting interrupted or chaotic accretion histories in both stellar-mass and supermassive black holes.

High-spin black holes exhibit unique relativistic properties due to the proximity of their innermost stable circular orbit (ISCO) to the event horizon. [12] This proximity enhances gravitational redshift and Doppler effects, causing the Fe Kα line to broaden and shift to lower energies. These distortions in the X-ray spectra are a direct consequence of the extreme gravitational field near fast-spinning black holes. [7]

In addition, steep emission profiles amplify these spectral features. The strong bending of light caused by the intense gravity near ISCO focuses X-rays on the innermost regions of the accretion disk, increasing the reflection fraction. This amplification enhances the visibility of relativistic distortions. This makes the Fe Kα line and the emission patterns reliable indicators of the black hole spin. Together, these observations confirm the utility of relativistic reflection methods for measuring spin and understanding accretion dynamics. [6]

6. Summary

The results of this study highlight the robustness of the relativistic reflection method for the measurement of black hole spin and the understanding of accretion dynamics. Figure 1 highlights the dominance of high-spin (≥0.8) systems in 33 black holes. This reflects the efficiency of sustained accretion processes and the role of angular momentum transfer in shaping black hole evolution. Figure 2, which focuses on stellar-mass black holes, shows that binary accretion is a key driver of high spins, where steady mass transfer aligns the accretion disk with the spin axis. In contrast, Figure 3, which examines supermassive black holes (SMBHs), shows that high spins result from prolonged disk accretion or aligned mergers in active galactic nuclei (AGN), processes that maintain or enhance angular momentum on cosmic timescales.

High spin systems consistently exhibit distinctive spectral features. These include broadened and redshifted Fe Kα lines and steep emissivity profiles. These features are driven by relativistic effects near the innermost stable circular orbit (ISCO). They are reliable indicators of spin. Moderate spin systems (0.4-0.6) are rarer and often associated with chaotic or interrupted accretion. Low spin systems (<0.4) are rare, highlighting the importance of sustained accretion for spin evolution.

This study confirms that the relativistic reflection method, with the support of advanced models such as RELXILL, is effective for both stellar-mass and supermassive black hole populations. Future research should focus on refining these models to account for complex accretion scenarios. It should also test this method on larger samples of black holes. Extending the use of relativistic reflection spectroscopy will improve our understanding of accretion physics and the interplay between spin and black hole evolution.