

Volume 106
Published on May 2025Volume title: Proceedings of the 3rd International Conference on Mathematical Physics and Computational Simulation
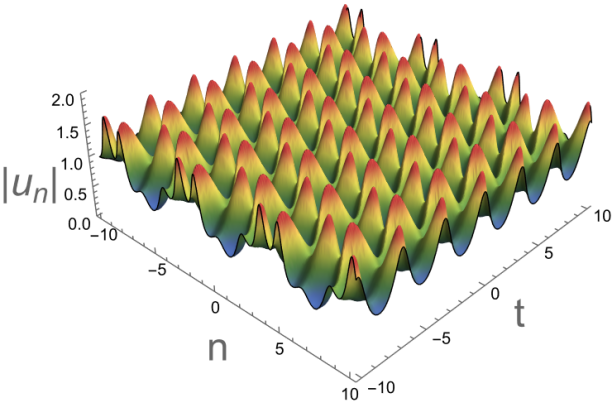
This study employs Hirota’s bilinear method to derive exact solutions for the coupled discrete non-local nonlinear Schrödinger (NLS) equation. The equation under investigation is derived from the non-local reduction of the coupled discrete nonlinear NLS equation, which arises in various physical contexts such as nonlinear optics and Bose-Einstein condensates. Exact solutions of coupled discrete non-local NLS equations are obtained, including bright-bright one-soliton solutions, two-soliton solutions, and dark-dark soliton solutions. For the dark-dark soliton solution, the construction of the solution and the bilinear expansion are derived from the continuous system, but the continuous system solved in this way yields a breathing solution, however, in this coupled discrete non-local NLS equation, under specific parameters, we obtain coupled dark-dark soliton waves. In addition, periodic solutions, singular solutions and double spatial period solutions are obtained by taking different parameters. The soliton dynamics are visualized using mathematical software, providing insights into their behavior and interactions. This work enhances the understanding of soliton solutions in discrete non-local systems and provides a practical approach for analyzing similar nonlinear wave phenomena.

 View pdf
View pdf


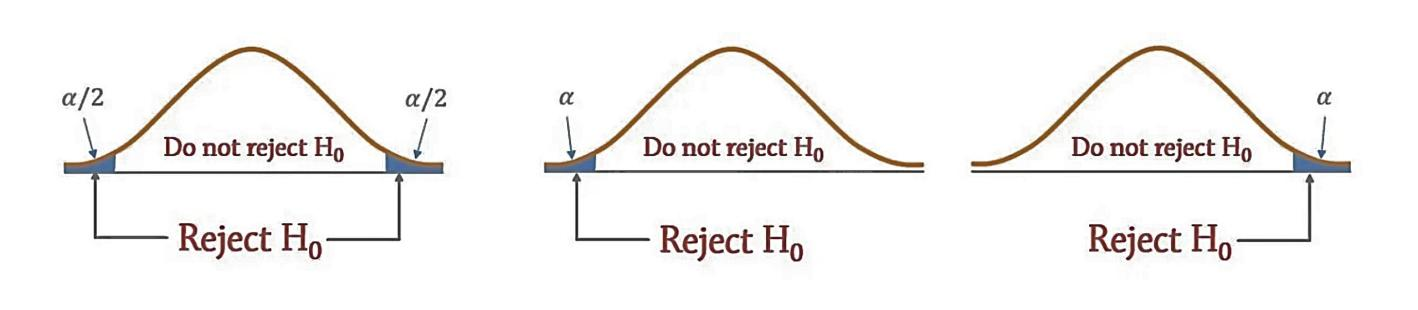
This paper explores the reasons and practical implications of hypothesis testing as an important tool for decision making in today's data-driven world. Beginning with the seminal work of Ronald A. Fisher in the early 1900s, the paper traces how the concepts of the null hypothesis and the p-value evolved into a formal framework. Through applications in fields as diverse as automotive engineering and product development to financial auditing and policy analysis, the focus is on how hypothesis testing can convert data from uncertainty to certainty. The methodology is particularly effective in situations where data are limited and where tools such as t-distributions help to balance the risk of Type I and Type II errors. In addition, the paper highlights the role of hypothesis testing in promoting objective, evidence-based decision making while minimizing personal bias. Finally, it provides a forward-looking perspective on the integration of real-time analytics and increased transparency in research practices, as well as on the development and outlook for future hypothesis testing methods. Overall, the findings suggest that hypothesis testing remains indispensable for resolving uncertainty and guiding reliable decision making in scientific research and common problems.

 View pdf
View pdf


This paper explores two systematic approaches for computing determinants of structured matrices using Laplace Expansion. The reduction (recursion) method leverages recursive expansion to decompose high-order determinants into lower-order counterparts, exploiting structural repetition. This method simplifies complex calculations by iteratively applying Laplace Expansion. The order-increase (edge) method strategically augments matrices with auxiliary rows and columns to transform them into solvable forms. Examples include converting a -order determinant into an upper triangular matrix and extending a -order matrix into a Vandermonde determinant, enabling direct evaluation via established formulas. Both methods highlight how Laplace Expansion, combined with matrix structure insights, streamlines determinant computation. The reduction method is ideal for matrices with recursive patterns, while the edge method benefits determinants missing key rows/columns but amenable to structural augmentation. Practical applications span linear algebra, physics, and cryptography, where efficient determinant evaluation is critical. The paper underscores the pedagogical and computational value of these techniques, offering educators and researchers accessible strategies for tackling high-order determinants. Future directions include integrating these methods with computational tools and exploring broader interdisciplinary applications.

 View pdf
View pdf


The Dirichlet integral is widely used in the fields of mathematical analysis, probability theory and physics. This paper explores the calculation of the generalized Dirichlet integral from zero to infinity. The author focuses on transitioning from special cases to deriving a general formula. The methodology used mainly include substitution and integration by parts. In the simplification of formulas, trigonometric identities and Frullani integral are also used. Moreover, the author obtains the general formula by discussing the odd and even power cases respectively. This paper deduces the general formula of Dirichlet integral by using Euler’s formula and binomial expansion. The result demonstrates that it uses special cases to find a general formula with the different order power and even the particular case of it, which is the same order power. The formula simplifies calculations. The significance of this paper lies in the calculation of Dirichlet integral general formula and various variations and give the answer. It provides an accurate formula for other studies using the this integral, and enhancing the overall body of knowledge in integral calculus.

 View pdf
View pdf


To explore the necessity and application strategies of economic mathematics in the financial and economic field, this paper adopts the literature review method. Based on previous research, the theoretical connotation of economic mathematics is systematically presented, its role mechanisms in risk assessment, investment decision-making, and option pricing are analyzed separately. Additionally, practical case analyses are conducted for rural financial institutions, securities companies, and futures companies. The study shows that through quantitative models and algorithm optimization, economic mathematics can accurately identify potential risks in financial activities, enhance the scientific nature of decision-making, assist rural financial institutions in optimizing credit resource allocation, and aid securities and futures companies in dynamic risk management and decision-making. The study further points out that the integration of economic mathematics with artificial intelligence, blockchain, and other technologies will promote the evolution of the financial and economic field towards intelligence and precision. The conclusions of this paper provide a theoretical basis and practical paths for financial institutions' risk prevention and innovation.

 View pdf
View pdf


Anime-style gacha games with card drawing mechanism as the core have shown great competitiveness in today's market, and pseudo-random algorithm is the core component of this card drawing mechanism. This paper uses data analysis research methods to mainly explore the composition of pseudo-random algorithms and their application in card drawing games. It aims to study the application effect of pseudo-random algorithms in card drawing games and their possible application areas. By analyzing the card drawing data published by game companies, explore the players' acceptance and preference for this algorithm, and then propose optimization solutions or further applications. Explore its application in a wider range of fields through analysis. This paper found that pseudo-random algorithms have played a positive role in the development and operation of card drawing games. On the premise of ensuring the fun of the random card drawing mechanism, it avoids the occurrence of extreme samples in a diversified way, and indeed guarantees the gaming experience of the vast majority of players.

 View pdf
View pdf


This study proposes a comprehensive medal prediction model for the 2028 Summer Olympics, providing valuable insights for the Olympic Committee. To achieve this, we conduct rigorous data preprocessing and analysis, employing K-means clustering to classify countries into distinct groups based on key attributes. We introduce an innovative evaluation framework that quantifies national competitiveness using weighted scores, forming the foundation for our medal prediction model, which integrates regression analysis and the Informer time-series model. A key focus of our research is to explore the relationship between sporting events and national medal counts by comparing Spearman correlation coefficients, while also empirically validating the host nation advantage. For medal table prediction, we implement a stacked ensemble model, combining linear regression, random forest, support vector regression (SVR), K-nearest neighbors (KNN), and XGBoost, ensuring robustness and accuracy. To address the first-time winning country problem, we reformulate it as a binary classification task using logistic regression, evaluating performance through accuracy metrics and confusion matrix analysis. Additionally, we investigate the “great coach” effect by modeling it as a maximum flow problem in graph theory, proving its existence via bottleneck capacity constraints. Furthermore, we conduct uncertainty quantification and hyperparameter tuning to enhance the model’s reliability and predictive performance. Our findings contribute to a data-driven understanding of Olympic medal distributions, offering a novel perspective on factors influencing national athletic success.

 View pdf
View pdf


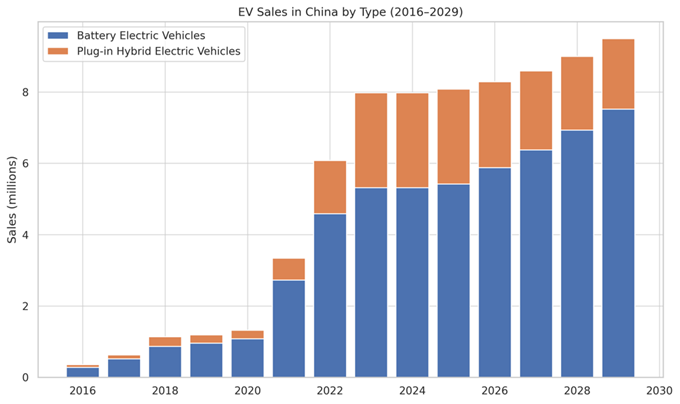
This research has studied how Chinese government subsidy programs affect EV sales throughout the years spanning from 2016 to 2023. The paper evaluates the connection between EV adoption rate increases and yearly public sector financial assistance through descriptive methods and data visualization. The time-based analysis demonstrates that EV sales increased rapidly when government subsidies grew stronger, validating the theoretical framework about subsidies promoting electric vehicle acceptance rates. Battery electric vehicles (BEVs) have taken the leading role in the electric vehicle market, which shows that buying preferences meet government policy objectives. The analyzed data suggests that after 2023, economic connections between government subsidy initiatives and EV market performance may be diminished. Research results demonstrate that subsidies drive market development in its initial phases, but policymakers should transition to long-term sustainable policies. Current market statistical data demonstrates constant BEV dominance, demonstrating the public interest in zero-emission transportation systems. The decreasing government support during 2023 failed to inhibit the continuing growth of EV sales, showing that the market was transitioning toward self-fuelled expansion rather than external incentives.

 View pdf
View pdf


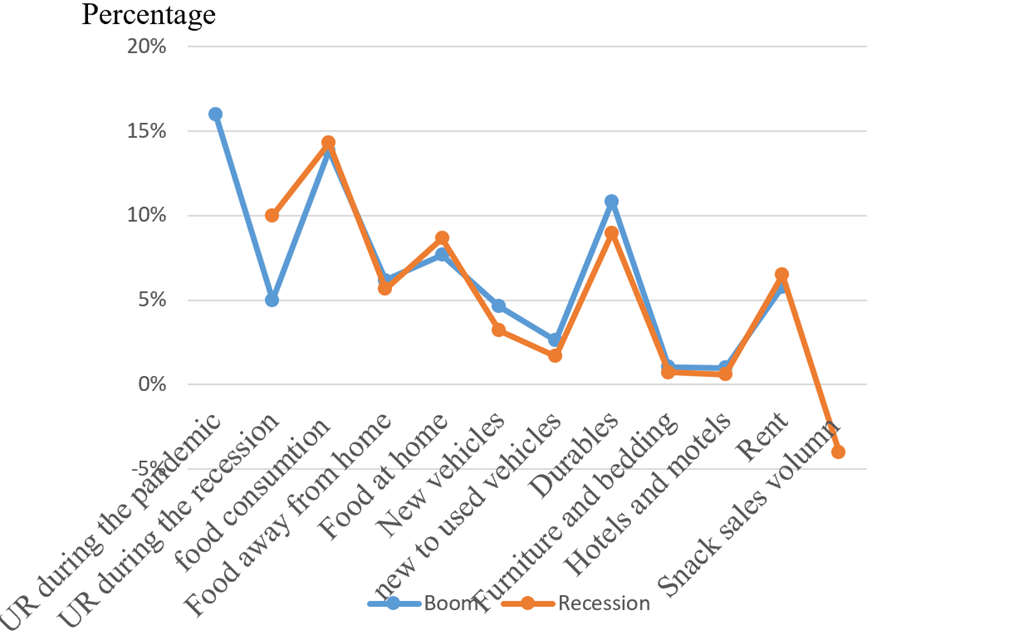
People’s consumption concepts are closely related to income and socio-economic conditions. When facing an economic recession, the recession reflected by the changes in GDP will not only affect the employment rate and the wage rate, but will further affect all kinds of commodities markets. The market can react in advance and minimize their losses if consumers’ perception of consumption and impacts brought through these changes can be predicted by analyzing economic indicators and trends of the economy. The Vector Auto Regression model will be used in this paper to further analyze different economic indicators that can reflect the changes and relationships of these factors that are affected by the economic downturn. These tools will be applied in this article to explore how factors can be affected by the economy and will further determine the market direction with the change of consumption concept under the trade-off and domination of consumers. Through analyzing the model, this paper concludes that the economic downturn can significantly reduce consumers’ willingness to buy and instead pay attention to wealth accumulation. The accuracy of the vertical auto regression model used in this paper does not have a high accuracy in analyzing relationships between each variable, thus it may not be the optimal choice to rely on to analyze the economic trend. Further models and variables should be put into consideration.

 View pdf
View pdf



This study investigates the motion characteristics of microswimmers in low Reynolds number environments through numerical simulation and theoretical analysis. A biomimetic microswimmer with a spherical head and helical tail was designed based on the Magariyama model. Using MATLAB programming, the fluid dynamics equations were solved to calculate the swimming velocity and propulsion efficiency under various helical parameters. The results demonstrate that the tail’s helical angle and wavelength significantly influence the swimmer’s propulsion performance. Furthermore, the study reveals the interplay between inertial and viscous forces at the microscale. These findings provide theoretical support for the application of microrobots in biomedical fields.

 View pdf
View pdf




