1. Introduction
In the game, randomness is everywhere. The results of randomness bring about contingency and uncertainty, which satisfy the players' sense of freshness and ensure the activity of the game. However, complete randomness will lead to differences in player experience. For example, people with good luck can draw rare items several times in a row, while people with bad luck may never draw them. This phenomenon has led to a decline in the experience and willingness of some players to play the game. To address this issue, pseudo-random algorithms are used. Game companies adjust the output of these algorithms to control the probability of item appearance, thereby avoiding extreme outcomes caused by pure randomness.
This approach ensures the relative rationality and fairness of the game mechanism and effectively stimulates players' desire to collect. This paper analyzes the basic principles of pseudo-random algorithms and their application in card drawing mechanisms by extensively referencing materials and data. Through case studies of typical card-drawing games, the paper explores the algorithm's impact on game operations and provides suggestions for optimization and future application. By studying the application and performance of pseudo-random algorithms in card drawing systems, this paper aims to enhance the fairness and enjoyment of games and assist developers in making targeted adjustments to support long-term game sustainability.
2. The basic principle of pseudo-random algorithm
2.1. Overview of basic principles
Pseudo-randomness is mainly achieved through a pseudo-random number generator (PRNG). By inputting a seed, a random number sequence can be obtained. Since this number sequence is generated using a certain algorithm and a certain seed, it means that the same number sequence can be generated through the same initial conditions (such as seeds), which is pseudo-randomness and is also contrary to true randomness, such as random numbers generated by physical processes.
PRNG has determinism and periodicity. Determinism is as mentioned above. Inputting the same seed can make PRNG output the same sequence of numbers. Periodicity means that the sequence will eventually repeat. Although this is not an ideal feature (meaning it is not truly random), PRNG is still used in practice because it is fast in generation and can output a large number of numbers in a short period of time.
2.2. Linear congruential generator
The linear congruential generator (LCG) is one of the oldest and most famous pseudo-random algorithms. It was published by Thomson in 1958 and Rotenberg improved the basic formula in 1960 [1-2]. LCG is defined by the following recursive formula:
\( X\_(n+1)=(aX\_n+c) mod m \) (1)
where X is a pseudo-random number, and
\( m,0 \lt m --the "modulus" \)
\( a,0 \lt a \lt m -- the "multiplier" \)
\( c,0≤ c \lt m -- the "increment" \)
\( {X_{0}},0≤{X_{0}} \lt m-- the "seed" or "start value" \)
When \( m \) is a prime number and c=0, the algorithm is called Lehmer RNG, named and published by D.H. Lehmar in 1951. Lehmer RNG can be regarded as a special case of LCG, with more restrictions than LCG, such as \( {X_{0}} \) must be coprime with \( m \) , etc. [3]. When c≠0, the algorithm is called a mixed congruential generator [4].
The advantages of the LCG algorithm are its concise code and extremely high computational efficiency at the time (the time complexity of generating a pseudo-random number is constant level). Its disadvantages are its pickiness about the parameter m. In actual operations, only the case where m is a power of 2 is considered to avoid a large number of modular operations. In terms of period, it is not as good as the Mersenne Twister algorithm, which has a longer period (usually \( {2^{19937}}-1 \) ), better mass distribution and more efficient operation [5-6].
The following code is a simple implementation of LCG in Python:
def lcg(m, a, c, seed): while True: seed = (a * seed + c) % m yield seed |
Where m, a, and c are Modulus, Multiplier, and Increment in Formula 1, respectively. Seed is the initial value that determines the starting point of the random number sequence. “yield seed” turns the function into a Python generator that continuously generates random numbers instead of calculating all the values at once.
3. The dynamics of probability in games
Pseudo-random algorithms are used in Dota 2 to represent statistical mechanisms for certain effects with a certain probability. The probability of an effect occurring in the Nth test after the last successful trigger is given by the following formula:
\( P(N)=C\cdot N \) (2)
This algorithm is also used in gacha games. Obviously, for each instance where a rare card is not drawn, this algorithm will increase the probability of drawing a rare card next time by the constant C. Constant C is also the initial winning probability, and the counter will be reset every time a rare card is drawn.
Consider that if we use a true random algorithm and set the winning rate to 25%, after 10 draws, there is still \( {(0.75)^{10}}=5.63\% \) of people still get nothing, which greatly affects the game experience of this part of unlucky players. Therefore, the advantage of the algorithm in Dota 2 is that it can stably guarantee the actual winning rate. The relationship between the actual winning probability and the C value is shown in Table 1 below:
Table 1: The relationship between the actual winning probability and the initial setting probability
Actual winning rate | C value |
5% | 0.00380165830355313910175646 |
10% | 0.01474584478107267587705081 |
15% | 0.03222091437308767497511735 |
20% | 0.05570404294978185185839865 |
25% | 0.08474409185231699027527480 |
Back to the assumption mentioned in the previous paragraph. To ensure that the actual winning rate is 25%, according to Table 1, the corresponding C value should be 0.08474409185231699027527480, which is approximately equal to 8.47%. After that, each time a rare card is not drawn, the probability increases by 8.47% and the counter increases by 1, until a rare card is drawn and the counter is reset, and the probability returns to the initial value of 8.47%.
Figure 1 shows the difference in expected draws between this pseudo-random algorithm and the true random algorithm (the blue one is the pseudo-random algorithm). It can be seen that the main function of pseudo-randomness is to concentrate the expected draws of players into one area, avoiding extreme situations and raising the lower limit of player experience in disguise. In contrast, the true random algorithm, in theory, has no upper limit on the number of draws. In the most extreme case, rare cards may never be drawn. As shown in the red part of Figure 1, under the operation of the true random algorithm, the expected draws of some players are far higher than the average, which leads to poor game experience and a decrease in the willingness to play, and ultimately leads to player loss.
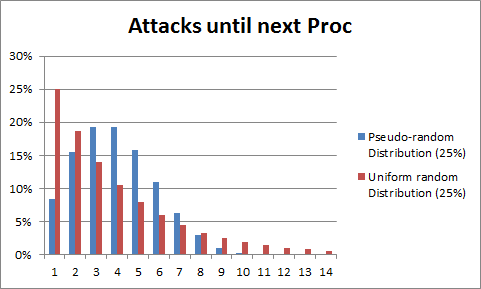
Figure 1: Comparison of expected draw numbers between pseudo-random and true random
4. Case analysis of pseudo-random algorithms in genshin impact
4.1. Basic working principle
In the Gacha game, the card pool contains cards of different rarities. The higher the rarity of the card, the lower the weight and the smaller the probability of winning.
Taking the game Genshin Impact as an example, the basic rate of 5-star characters is only 0.600%, and the basic rate of 4-star characters is 5.100%. When a 5-star character is drawn, there is a 50% probability that it is a limited character of the current period, and the other 50% is a permanent 5-star character. Obviously, the probability of drawing a limited 5-star character is not high, or even very low. In order to satisfy the player's psychology to the greatest extent while promoting player consumption, and to prevent players from being disappointed by not being able to draw rare cards, the game development department introduced a guarantee mechanism in the card drawing system.
4.2. Bottom-line guarantee mechanism
The guarantee mechanism in the card-drawing game can be roughly divided into two categories according to the different objects of the code: soft guarantee and hard guarantee. Soft guarantee means that if the player still does not get a rare character after multiple consecutive card draws, the system will increase the probability of rare items appearing. Hard guarantee means that when the player reaches a certain number of card draws but still does not draw a rare card, the system will force a rare card to drop. As mentioned in chapter 3, if the role of pseudo-randomness is to increase the lower limit in disguise, then the guarantee mechanism is more like a lock.
Back to the example of Genshin Impact mentioned earlier, its guarantee mechanism is a kind of hard guarantee, which is set to obtain a 5-star character for up to 90 card draws and a 4-star or higher item for up to 10 card draws. After adding the guarantee mechanism, the overall probability of obtaining a 5-star character increased to 1.600%.
4.3. Impact and player feedback
Relatively speaking, the guaranteed mechanism balances the experience of some players with bad luck, ensuring that players can stably obtain rare cards in uncertain draws, which in turn has a positive impact on the fairness of the game. At the same time, the novelty and uncertainty of the algorithm also bring more profits to the game. According to Sensor Tower data, Genshin Impact attracted $245 million in the first month of its launch; in the first year of its launch, the total revenue on Google Play and App Store reached $2.3 billion. It is not difficult to see from the data that, as a game that uses card drawing as the main means of profit, the pseudo-random algorithm has a positive impact on players' consumption and willingness to play.
5. Optimization of pseudo-random algorithms
Although the pseudo-random algorithm has greatly optimized the card drawing environment, avoiding too unlucky situations, and adding a guaranteed mechanism to give players a "visible" bottom line. In order to give players a better gaming experience and ensure their satisfaction with the game, the game development team has made many optimizations based on the previous article.
Back to the example of Genshin Impact mentioned above. If the 5-star character obtained in this card drawing is not a limited 5-star character, then the 5-star character obtained in the next card drawing must be a limited 5-star character. Not only that, the development team also added a "capture light" mechanism, with a basic probability of 0.018%. In the case of triggering "Capturing Radiance", the probability of obtaining a limited 5-star character when drawing a 5-star character increases from 50% to 55%, further increasing the probability of drawing the desired character.
6. Conclusion
This paper mainly discusses the application of pseudo-random algorithms in card-drawing games. It proves the significant role of pseudo-random algorithms in attracting players and improving the playability of games. This paper has not yet explored the player satisfaction survey in depth, and has not used methods such as questionnaires to analyze the players' specific acceptance of pseudo-random algorithms and their actual game experience. In the future, pseudo-random algorithms will play a role in various fields, such as algorithm encryption and traffic signal control.
References
[1]. W. E. Thomson, A Modified Congruence Method of Generating Pseudo-random Numbers, The Computer Journal, Volume 1, Issue 2, 1958, Page 83, https://doi.org/10.1093/comjnl/1.2.83
[2]. A. Rotenberg. 1960. A New Pseudo-Random Number Generator. J. ACM 7, 1 (Jan. 1960), 75–77. https://doi.org/10.1145/321008.321019
[3]. Lehmer, D.H. (1951) Mathematical Methods in Large-Scale Computing Units. The Annals of' the Computation Laboratory of Harvard University, 26, 141-146.
[4]. Knuth, D. E. (1997). The art of computer programming (3rd ed.). Addison Wesley.
[5]. Steele, Guy & Vigna, Sebastiano. (2021). Computationally easy, spectrally good multipliers for congruential pseudorandom number generators. Software: Practice and Experience. 52. 10.1002/spe.3030.
[6]. Matsumoto, M., & Nishimura, T. (1998). Mersenne twister: a 623-dimensionally equidistributed uniform pseudo-random number generator. ACM Trans. Model. Comput. Simul., 8, 3-30.
Cite this article
Huang,J. (2025). Application of Pseudo-Random Algorithm in Card Drawing Games. Theoretical and Natural Science,106,40-44.
Data availability
The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.
Disclaimer/Publisher's Note
The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
About volume
Volume title: Proceedings of the 3rd International Conference on Mathematical Physics and Computational Simulation
© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and
conditions of the Creative Commons Attribution (CC BY) license. Authors who
publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons
Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this
series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published
version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial
publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and
during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See
Open access policy for details).
References
[1]. W. E. Thomson, A Modified Congruence Method of Generating Pseudo-random Numbers, The Computer Journal, Volume 1, Issue 2, 1958, Page 83, https://doi.org/10.1093/comjnl/1.2.83
[2]. A. Rotenberg. 1960. A New Pseudo-Random Number Generator. J. ACM 7, 1 (Jan. 1960), 75–77. https://doi.org/10.1145/321008.321019
[3]. Lehmer, D.H. (1951) Mathematical Methods in Large-Scale Computing Units. The Annals of' the Computation Laboratory of Harvard University, 26, 141-146.
[4]. Knuth, D. E. (1997). The art of computer programming (3rd ed.). Addison Wesley.
[5]. Steele, Guy & Vigna, Sebastiano. (2021). Computationally easy, spectrally good multipliers for congruential pseudorandom number generators. Software: Practice and Experience. 52. 10.1002/spe.3030.
[6]. Matsumoto, M., & Nishimura, T. (1998). Mersenne twister: a 623-dimensionally equidistributed uniform pseudo-random number generator. ACM Trans. Model. Comput. Simul., 8, 3-30.









