1. Introduction

Dynamic inverse problems are prevalent in signal processing, fluid mechanics and system control. However, due to their nonlinear and dynamic nature, ordinary analysis cannot easily deal with these issues. For dynamic inverse problems, BPNN (machine learning based) back propagation neural network has gained significant popularity in recent years for its powerful nonlinear fit [1]. But classical EVO still suffers from population sparsity loss, slower convergence, and a lack of dynamical adaptability under dynamic situations. To overcome these issues, this paper suggests evolutionary algorithm that routinely improves BPNN performance with a dynamic population adjustment algorithm, multi-objective optimization model, and environmental adaptability update strategy. The experiment uses nonlinear dynamic system control, dynamic signal reconstruction, and fluid mechanics inverse problems as testing problems, and rigorously tests the algorithm on optimisation, dynamic adaptability, and robustness to bring forth a new method to solve dynamic inverse problems.

2. Literature Review

Scientists studied dynamic inverse problem-solving techniques for many years. Traditional methods like regularization and optimization work well to solve inverse problems when the environment stays stable. The methods work well for basic conditions but struggle with advanced problems when the environment keeps changing. Back propagation neural networks (BPNN) stand out as machine learning tools because they process nonlinear tasks and adjust to various situations better than other methods. The diagram in Figure 1 shows how BPNN processes input data through hidden layers before calculating the output. The main benefit of BPNN comes from its ability to update weights during training thanks to backpropagation which helps the system learn from intricate datasets. Scientists now combine evolutionary optimization algorithms with neural networks to make them work better [2]. Figure 2 shows the basics of Genetic Algorithms with genes arranged in chromosomes that evolve across generations through natural selection and genetic mixing. GA shows strong results with stable tasks yet runs into diversity problems when handling dynamic settings [3]. Particle swarm optimization performs global searches by modeling group behavior yet needs longer time to find solutions when handling many input variables [3]. Although many people use differential evolution it struggles to escape local optima solutions in dynamic inverse problem situations. Although progress has been made in these areas, a significant challenge remains: Finding the best way to solve dynamic optimization problems while maintaining high-quality results and fast completion times.

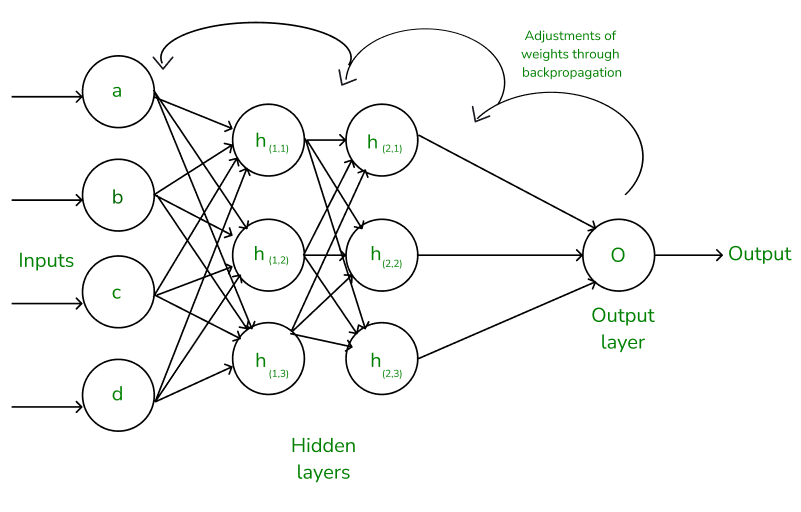
Figure 1: Structure of Back Propagation Neural Network (BPNN) and the Backpropagation Process (Source:geeksforgeeks.org)

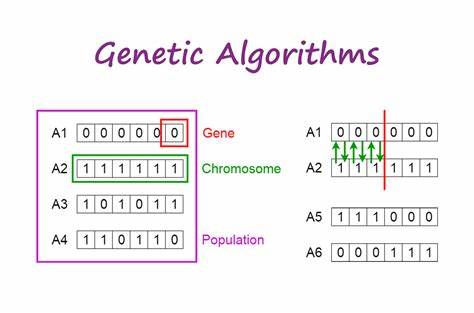
Figure 2: Overview of Genetic Algorithm: Genes, Chromosomes, and Population Evolution(Source: towardsdatascience.com)

3. Experimental Methods and Design

3.1. Improved EVO Algorithm

This study systematically improves the traditional evolutionary optimization algorithm (EVO) to solve the problems of population diversity loss, insufficient adaptability and low optimization efficiency in dynamic inverse problems. First, a dynamic population diversity maintenance mechanism is proposed. The population structure is analyzed in real time and the mutation rate and crossover rate are dynamically adjusted by introducing an entropy-based diversity monitoring method. Secondly, an environmental adaptability update strategy is designed, which combines genetic memory technology with a dynamic perturbation method to quickly adjust the population search direction [4]. Finally, this study constructed a multi-objective optimization framework, taking error minimization, model complexity reduction and convergence efficiency improvement as optimization goals. The optimization is mainly global search in the early stage, and gradually focuses on local optimization in the later stage to achieve a balance between global search and local refinement by dynamically adjusting the weights of each goal in stages. These improvements jointly improve the adaptability and solution efficiency of the EVO optimized BPNN model in dynamic inverse problems.

3.2. Experimental Scenarios and Data Sources

The experimental design covers three typical dynamic inverse problem scenarios to fully verify the effectiveness and robustness of the improved EVO algorithm. The first category is the nonlinear dynamic system control problem, which is based on the Lorenz chaotic system, simulates dynamic parameter changes, and generates input and output data. The second category is the dynamic signal reconstruction problem, which evaluates the optimization ability of the algorithm in the signal processing scenario[5]. This scenario simulates the characteristics of the real signal with constantly changing frequency and amplitude in a dynamic environment, which is used to verify the adaptability and accurate reconstruction ability of the improved EVO algorithm to dynamic data patterns. The third category is the inverse problem of dynamic fluid mechanics. Data is generated through fluid dynamics simulation, and the dynamic characteristics of complex flow fields are reconstructed based on limited observation points [6]. This experimental scenario mainly tests the performance of the algorithm in high-dimensional complex optimization problems, especially the accuracy and efficiency of the reconstruction of flow field boundary conditions. Being derived from standard public data sets and custom simulations, the experimental data ensures the comprehensiveness and objectivity of the results.

3.3. Performance Evaluation Indicators

The improved EVO algorithm in different dynamic inverse problem scenarios, a comprehensive and objective performance evaluation indicator system is designed. First, the convergence speed is an important criterion for evaluating the efficiency of the algorithm, and the time cost of the algorithm to reach the optimal solution is measured by the number of iterations. The design goal of the improved EVO is to significantly reduce the number of iterations while ensuring accuracy. Secondly, the optimization accuracy is measured by the relative error between the objective function value and the actual solution, indicating the algorithm's ability to solve in complex dynamic scenarios. Dynamic adaptability is another key indicator used to evaluate the algorithm's ability. To respond quickly to environmental changes, the stability of the algorithm is reflected by measuring the performance fluctuation amplitude and adjustment time. Finally, robustness is tested through the consistency of multiple sets of experimental results to analyze the impact of different initial conditions on the algorithm results [7]. Table 1 below summarizes key performance indicators for the improved EVO algorithm.

Table 1: EVO Algorithm Performance Evaluation

4. Experimental Results and Data Analysis

4.1. Nonlinear Dynamic System Control

The improved EVO-BPNN showed significant performance advantages in nonlinear dynamic system control experiments. Experimental data shows that the average error of this algorithm is 0.026. Compared with 0.085 of PSO, the optimization accuracy has been greatly improved. At the same time, the convergence speed of the improved algorithm is significantly improved, and a stable solution can be achieved with only 40 iterations, which is about 28% less iterations than traditional EVO. Through the dynamic population diversity maintenance mechanism, the algorithm can effectively maintain the global exploration ability of the population in the early stage of search and avoid falling into local optimality. In the later stage of search, the dynamic adjustment mechanism enhances the accuracy of local search. In addition, experimental results show that even in complex dynamic parameter changing scenarios, the performance of the improved EVO-BPNN still maintains a high degree of stability [8]. This shows that the algorithm not only has good adaptability when dealing with nonlinear dynamic system control problems, but also achieves an effective balance between global search and local optimization. Table 2 shows the performance comparison between the improved EVO-BPNN and traditional EVO and PSO in the nonlinear dynamic system control experiment.

Table 2: Nonlinear Dynamic System Control Performance

4.2. Dynamic Signal Reconstruction

In the dynamic signal reconstruction experiment, the improved EVO-BPNN performed equally well, with a reconstruction error of only 0.012, while the errors of traditional methods were higher than 0.035. The experimental scenario simulated a complex environment in which the signal frequency dynamically changed within the range of [0.5Hz, 3Hz]. The results showed that the improved algorithm could quickly capture frequency changes and achieve accurate reconstruction. Especially in the case of signal mutations, the algorithm shows strong adaptability, and its optimization time is shortened by about 35% compared with traditional methods, reflecting a significant improvement in efficiency. This superior performance is mainly attributed to the introduction of the environmental adaptive update strategy, which not only enhances global search capabilities through the combination of dynamic perturbation and genetic memory, but also improves the ability to respond quickly to local changes in the dynamic environment [9]. Experimental results show that the improved EVO-BPNN can achieve higher optimization accuracy and efficiency in dynamic signal processing, providing a reliable solution. Table 3 shows the performance comparison between the improved EVO-BPNN and the traditional method in the dynamic signal reconstruction experiment.

Table 3: Dynamic Signal Reconstruction Performance

4.3. Inverse Problem of Dynamic Fluid Mechanics

In experiments on inverse problems of dynamic fluid mechanics in high-dimensional complex environments, the performance of the improved EVO-BPNN is particularly outstanding. Experimental results show that the mean error of the algorithm is 0.024 and the standard deviation is only 0.008, which is significantly lower than the mean error (0.038) and standard deviation (0.015) of traditional EVO. This result shows that the improved algorithm not only has higher accuracy but also shows strong stability in high-dimensional dynamic scenes. The dynamic perturbation mechanism can quickly adjust the search direction when the environment changes, and the genetic memory module accelerates the convergence process of the global optimal solution by guiding the population to move closer to the historical optimal solution [10]. In addition, experiments also show that under more complex flow field boundary conditions, the robustness of the improved algorithm is still superior, and the error fluctuation range of multiple experimental results remains at a low level. Figure 3 demonstrates that the improved algorithm significantly outperforms the traditional algorithm in both the mean error and standard deviation metrics, showing higher accuracy and stability.

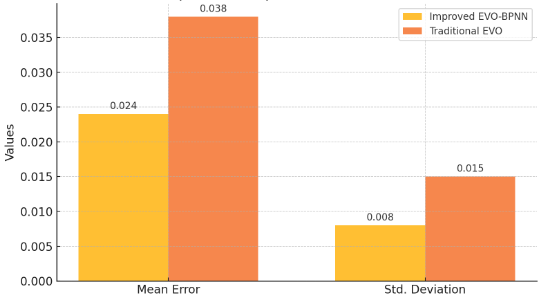
Figure 3: Performance Comparison

5. Discussion

5.1. Algorithm Advantages and Improvements

In this study the improved evolutionary optimization algorithm proposed shows excellent performance advantages in solving dynamic inverse problems. And its innovative design significantly improves the algorithm's global search capability, dynamic response capability, and optimization efficiency. At the same time, the environmental adaptability update strategy significantly improves the algorithm's ability to respond quickly to environmental changes. Ensuring that the population can adjust the search direction in a timely manner in dynamic scenarios and maintain stable optimization performance by combining genetic memory and dynamic perturbation methods [11]. In addition, the multi-objective optimization framework meets the diverse needs in dynamic inverse problems through dynamic equilibrium error minimization, model complexity control and convergence speed, making the algorithm more comprehensively adaptable in complex environments. Remarkable effects in experiments have been shown by these innovative designs, including the verification of the algorithm's wide applicability and efficiency in nonlinear system control, dynamic signal reconstruction, and inverse problems of fluid mechanics.

5.2. Limitations and Future Directions

Although the improved EVO algorithm has achieved significant results in several experimental scenarios, there are still some limitations that need to be further optimized. First, the computational complexity of the algorithm is high, and it relies more on hardware resources when dealing with high-dimensional dynamic problems, which may bring certain challenges to the promotion of practical applications. Second, the selection of dynamic perturbation parameters has a large impact on the performance of the algorithm, and the current parameter adjustment mainly relies on empirical settings, lacks a high degree of adaptivity, and may not perform stably enough in some special scenarios. Therefore, future research can focus on exploring automated parameter tuning strategies to further improve the robustness and generalization ability of the algorithm by introducing adaptive control mechanisms [12]. In addition, in order to reduce the computational cost, trying to combine distributed computing or multi-threading technology, from the hardware and software level to jointly optimize the efficiency of the algorithm.

6. Conclusion

The study significantly enhances the global search capability, dynamic adaptation capability and convergence efficiency of the algorithm by introducing the dynamic population diversity preservation mechanism, the environment adaptive updating strategy, and the multi-objective optimization framework. The experimental results show that the improved EVO-BPNN exhibits excellent performance in nonlinear dynamic system control, dynamic signal reconstruction and hydrodynamic inverse problems, with higher optimization accuracy and adaptability, and the convergence speed is significantly improved compared with the traditional method, which verifies the validity and robustness of the method. This study not only provides an efficient technical solution for solving dynamic inverse problems, but also provides strong support for the development and practice of optimization algorithms.