1. Introduction

The core of the insurance industry lies in risk transfer and allocation, and its mathematical foundation relies on the two pillars of probability theory: the Law of Large Numbers (LLN) and the Central Limit Theorem (CLT). LLN guarantees the stability of long-term expected losses through convergence, while CLT provides a quantitative tool for short-term fluctuations through a normal distribution. Traditional insurance models are mostly based on independent and equally distributed assumptions, while actual risks are often correlated (for example, natural disasters lead to simultaneous claims in multiple regions). This paper explores the adaptability of classical theories in modern insurance scenarios by extending independent risk models and machine learning techniques.

Wang showed that the maximum amount of third-party liability insurance in auto insurance is set at 200,000 yuan, which is behind the joint effect of CLT and LLN [1]. When the number of insured subjects is large enough, the insurance company calculates the extreme probability of payment through CLT, and combines the convergence of LLN to ensure long-term profit stability. This conclusion provides a theoretical basis for the insurance industry's premium limitation. In addition, Tang verified the universality of the law of large numbers through lottery examples, revealing the regularity of random events under large samples, and further supporting the feasibility of insurance risk pooling [2].

The rest of this paper is organized as following. In section 2, the author will introduce the method and theory. Next, section 3 is devoted to results and applications. Finally, the last section gives a conclusion.

2. Method and Theory

2.1. Law of Large Numbers and Central Limit Theorem

By setting independent identically distributed (i.i.d.) random variable sequence \( { X_{1}} \) , \( {X_{2 }} \) ,..., \( {X_{n }} \) , whose expectation is μ, then the sample mean converges to the expectation with probability:

\( \underset{n→∞}{lim}P( | \frac{1}{n}\sum _{i=1}^{n}{X_{i}}-μ| \lt ε)=1.\ \ \ (1) \)

This is the weak law of large numbers. Sinchin's Law of large numbers further relaxes the conditions, only the expectation exists, and is applicable to the thick tail distribution scenario.

For insurance applications, the first is about premium pricing, estimating expected losses from historical claims data E[X], to ensure that premiums cover long-term costs. For example, in the case of auto insurance, Wang predicted the average payout amount through LLN and designed the premium structure combined with the safety additional amount [3]. Second is about risk pooling, the number of subjects when insured n is large enough, the actual loss rate approaches the theoretical probability (such as mortality).

Sequence of random variables for i.i.d. \( { X_{1}} \) , \( {X_{2 }} \) ,..., \( {X_{n }} \) , whose mean is μ, the variance is \( {σ^{2}} \) , Then the standardized sample mean converges to the standard normal distribution according to the distribution:

\( \frac{\overline{X}-μ}{σ/\sqrt[]{n}}\overset{d}{→}N(0,1)\ \ \ (2) \)

The Lindeberg-Levy CLT is its classical form, which requires finite variance. For insurance applications, the first is about reserve calculation, total claims paid \( S=∑{X_{i}} \) , approximate obedience \( N(nμ,n{σ^{2}}) \) , to estimate the probability of extreme losses. Wang proposed that CLT was used to calculate the additional safety factor λ, which ensures that insurance companies avoid losses with a 95% probability [4]. The second is about confidence interval construction, calculating the margin of safety for premium adjustment based on normal distribution.

2.2. Contrast of similarities and differences

The Comparison of theorem of large numbers and central limit theorem is shown in Table 1. As two cornerstones of probability theory, Central Limit theorem (CLT) and Law of large Numbers (LLN) show remarkable commonality in both theory and application. First, both require that the sequence of random variables satisfy the basic assumption of an independent identical distribution (i.i.d.), a condition that provides mathematical rigor for statistical inference. Second, they are both suitable for analyzing the collective behavior of a large number of random variables: LLN characterizes long-term stability through the convergence of the sample mean, while CLT quantifies short-term volatility through a normal approximation. In practice, they have irreplaceable value in risk modeling and data analysis in insurance, finance, medicine and other fields. For example, insurance companies use LLN to predict the long-term average loss ratio to set premiums, while CLT to estimate the extreme loss probability to determine the size of reserves. The synergistic effect of the two forms the theoretical basis of modern actuarial science [3, 5].

Table 1: Comparison of theorem of large numbers and central limit theorem

Although both CLT and LLN are based on the assumption of independent co-distribution, their core concerns and application scenarios are fundamentally different. From the perspective of mathematical connotation, LLN emphasizes that the sample mean converges to the expected value according to probability \( {\bar{X}_{n}}_{→}^{p}μ \) , while CLT reveals that the distribution of the standardized sample mean converges to the normal distribution \( {\bar{Z}_{n}}_{→}^{d}N(1,0) \) . This difference leads directly to the divergence of its application goals: LLN is used primarily to verify theoretical expected values (e.g., mortality, frequency of claims), while CLT is used to construct confidence intervals or calculate the probability of extreme events (e.g., bankruptcy risk). Moreover, the mathematical requirements for the two are different - CLT requires a finite variance to guarantee the validity of a normal approximation, whereas LLN requires only the expected existence (as in Sinchin's Law of large numbers). Taking insurance solvency analysis as an example, LLN can predict the average number of deaths, while CLT further calculates the probability that the number of deaths exceeds the threshold, thus providing a quantitative basis for capital adequacy regulation [4, 6].

Combining the advantages of CLT and LLN, the multi-dimensional analysis of random phenomena can be realized. In the insurance industry, LLN provides a long-term equilibrium benchmark for premium pricing, while CLT quantifies risk exposure through a normal distribution, and the combination of the two can optimize risk management strategies (such as safety add-on factor design). Further, modern risk theories have broken through the traditional assumption of independent and same distribution. For example, Copula model extends the application boundary of CLT by describing the correlation between variables [7], while machine learning techniques (such as random forest) integrate the convergence idea of LLN to improve the accuracy of individual risk assessment. Future research could explore the adaptability of non-parametric CLT in high-dimensional data, or combine deep learning models to enhance the robustness of LLN in non-stationary environments. These advances will promote the application of probability theory in complex systems such as artificial intelligence and climate prediction, demonstrating its interdisciplinary value.

2.3. Extension of independent risk model (Copula theory)

The traditional CLT assumes that risks are independent, but in practice (such as regional disasters) risks are often correlated. Copula model provides a flexible risk modeling tool by separating the correlation structure and edge distribution between variables [8].

Let the marginal distributions of two risk variables X and Y be \( {F_{X}}(x) \) and \( {F_{Y}}(y) \) , respectively, and their joint distributions can be expressed as:

\( {F_{X,Y}}(x,y)=C({F_{X}}(x),{F_{Y}}(y))\ \ \ (3) \)

where \( C(u,v) \) is the Copula function. For a Gaussian Copula, the form is:

\( {C_{ρ}}(u,v)={Φ_{ρ}}({Φ^{-1}}(u),{Φ^{-1}}(v))\ \ \ (4) \)

where ρ is the correlation coefficient and \( {Φ_{ρ}} \) is the bivariate normal distribution function. For application significance, Copula was used to generate relevant risk samples and analyze the distribution of total loss S=X+Y. And the value at risk (VaR) under independent and non-independent hypotheses is compared to reveal the amplification effect of correlation on extreme events.

3. Results and Application

3.1. Auto Insurance Premium Pricing and Risk Reserve

For the problem setting, an insurance company covers 10,000 vehicles, each vehicle annual loss \( {X_{i}}∼Exp(λ) \) , needs to determine the total reserve H so that the probability of underpayment is less than 5%. For the LLN applications, the expected total loss is \( E[S]=n/λ \) . When n is large enough, the actual payout S fluctuates around E[S] [9]. For the CLT applications, By CLT, \( S≈N(n/λ,n/{λ^{2}}) \) . If \( Z=\frac{S-n/λ}{\sqrt[]{n/λ}} \) , then,

\( P(S \gt H)=P(Z \gt \frac{H-n/λ}{\sqrt[]{n/λ}})=0.05⇒H=\frac{n}{λ}+1.645\cdot \sqrt[]{\frac{n}{λ}}\ \ \ (5) \)

As a calculation example, if \( n=10,000,λ=0.01 \) , then \( H= 1,000,000+1.645×316.23≈1,052,000 \) .

Wang further analyzed the limitation of the amount of third-party liability insurance [6]. Assuming that an insurance company underwrites 10,000 policies and the probability of death \( p=0.001 \) , the CLT calculation shows that when the insured amount exceeds 200,000 yuan, the profit of the insurance company decreases rapidly with the increase of the number of deaths. For example, when the number of deaths is 13, the profit corresponding to 200,000 yuan of insurance is 7.61 million yuan, while the loss of 1 million yuan of insurance is 130,000 yuan. This result explains why insurance companies limit the maximum coverage to 200,000 yuan.

3.2. Prediction of Medical Expenses in Health Insurance

For problem setting, 100,000 enrollees in certain area \( {X_{i}}~ Γ(k=2,θ=1000) \) , each annual medical cost A, need to assess the probability that the total cost exceeds 210 million yuan. For LLN Perspective, the long-term average total cost is approaching \( E[S] = nkθ = 2 × {10^{8}} \) [10]. For the CLT calculation, by CLT, total cost \( S ≈ N(2 × {10^{8}}, 2 × {10^{11}}) \) , then

\( P(S \gt 2.1×{10^{8}})=1-Φ(\frac{2.1×{10^{8}} - 2 × {10^{8}}}{\sqrt[]{2 × {10^{11}}}})≈1-Φ(2.236)=1.27\%\ \ \ (6) \)

In conclusion, the probability of extreme overspending is low, which verifies the robustness of the insurance pool.

For simulation method, Gaussian Copula is used to generate random variables X and Y with correlation coefficient ρ = 0.7, whose edge distribution is exponential. A typical example is shown in Figure 1.

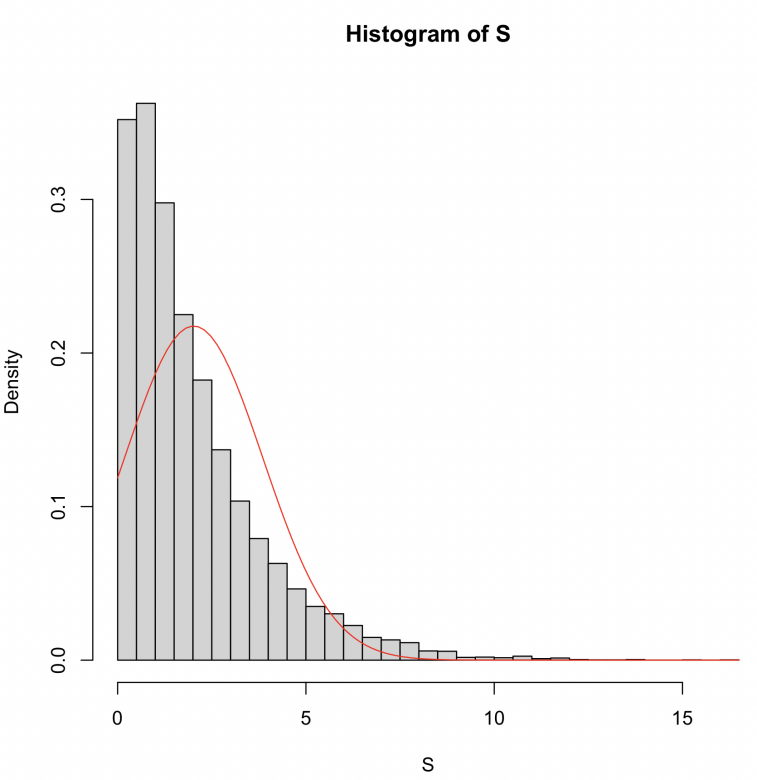
Figure 1: Total loss analysis under the independent risk model.

The results that the right tail of the total loss distribution is thicker than the normal distribution, indicating that the correlation exacerbates the extreme risk. Reserve strategies need to be adjusted to cope with potentially high payouts.

4. Conclusion

The Central Limit Theorem (CLT) and the Law of Large Numbers (LLN) serve as dual pillars in the insurance industry, with LLN ensuring long-term stability through expectation convergence and CLT quantifying short-term risks via normal distribution approximations. By integrating Copula models to address correlated risks and machine learning techniques like random forests for individualized claim predictions, this study bridges classical probability theory with modern data-driven approaches. For example, random forests refine granular risk assessments, while CLT aggregates total risk distributions to calculate extreme payout probabilities, enabling dynamic premium adjustments and efficient capital allocation. Wang’s work further validates that CLT-enhanced safety load calculations and expanded underwriting scales significantly improve solvency, demonstrating the synergy of theoretical rigor and practical adaptability in actuarial science.

Future research should focus on three frontiers, the first one is leveraging Generative Adversarial Networks (GANs) to simulate loss data, enhancing predictive accuracy in low-data scenarios; the second is developing high-dimensional Copula models to unravel complex risk interdependencies (e.g., climate-economic-health linkages); and the final one is deploying reinforcement learning for real-time, adaptive premium strategies. Additionally, as InsurTech advances, ensuring the robustness of CLT and LLN in distributed and heterogeneous data environments will be critical. These innovations, coupled with ethical AI frameworks, could redefine risk governance, enabling insurers to balance profitability with societal resilience. Ultimately, fusing classical theorems with cutting-edge technologies promises transformative breakthroughs in sustainable insurance solutions.