1. Introduction

In recent years, studies on the prediction of kidney stones based on urinalysis have gradually shifted from the detection of traditional biochemical indicators to multidimensional characterization [1]. Existing studies have confirmed that the concentrations of biochemical components such as calcium, oxalic acid, and uric acid in urine are closely related to calcium oxalate crystal formation, but these indicators alone have limited sensitivity and specificity for prediction. Meanwhile, the physical characteristics of urine (e.g., pH, specific gravity, turbidity, conductivity, etc.) are gradually gaining attention. However, most studies are still dominated by single-factor statistical analysis, and the mechanism of multifactorial interaction has been insufficiently explored [2]. In addition, traditional statistical models have bottlenecks in the capture of complex nonlinear relationships, which leads to difficulties in breaking through the prediction accuracy. In recent years, some studies have begun to try to integrate biochemical indicators and physical features, but the data fusion methods and dynamic monitoring techniques still need to be optimized [3].

Machine learning algorithms have shown significant advantages in kidney stone prediction research, especially in dealing with high-dimensional, nonlinear data. First, supervised learning models (Random Forest, Support Vector Machine, Gradient Boosting Tree) are able to integrate urinary biochemical indicators (calcium, oxalic acid concentration) with physical features (pH, conductivity), and reveal the key predictors through feature importance ranking. Second, deep learning models (e.g., convolutional neural networks) can process urine microscopy image data to automatically identify morphological features of calcium oxalate crystals (e.g., birefringence, cluster size), which can make up for the subjective defects of manual microscopy [4]. In addition, reinforcement learning has potential in dynamic monitoring scenarios, such as predicting the risk of stone formation and optimizing intervention strategies by analyzing the temporal changes of patients' urine parameters in real time. In this paper, we optimize the XGBoost algorithm based on the Newton-Raphson algorithm for risk prediction of kidney stones [5].

2. Data set sources and data analysis

This paper conducts experiments using an open source dataset that can be used to predict the presence of kidney stones based on urinalysis. The dataset contains 79 urine specimens to determine if certain physical characteristics of urine are associated with the formation of calcium oxalate crystals. The six physical characteristics of urine are density of urine relative to water, negative logarithm of hydrogen ions, osmolality, conductivity , urea concentration, and calcium concentration. A partial dataset was demonstrated as shown in Table 1.

Table 1: Part of the dataset.

3. Method

3.1. Vector Weighted Average Algorithm

The Newton-Raphson optimization algorithm is an efficient numerical optimization method based on second-order derivative information, and its core idea is to quickly approximate the extreme value point by local quadratic approximation of the objective function. Different from the traditional gradient descent method that only utilizes the first-order derivatives, the method achieves higher precision parameter updates in a single iteration by constructing the second-order Taylor expansion of the objective function and simultaneously considering the function curvature information during the iteration process. Specifically, the algorithm assumes that the objective function can be approximated as a quadratic form in the vicinity of the current iteration point, and determines the search direction and step size of the next step by solving the minima of this quadratic model. This quadratic approximation property allows Newton's method to have quadratic convergence speed when approaching the optimal solution, which is significantly better than the linear convergence property of the gradient descent method [6].

The specific implementation of the algorithm is divided into three key steps: first, the gradient and Hessian matrix of the objective function at the current parameter point are calculated, then the system of linear equations derived from the quadratic approximation model is solved to determine the direction of the update, and finally the parameter update is carried out along this direction. The mathematical expression is:

\( {θ_{k+1}}={θ_{k}}-H-¹({θ_{k}})∇f({θ_{k}}) \)

where H-¹ denotes the inverse of the Hessian matrix matrix.

This updating method essentially zeroes the gradient vector by adjusting the parameters, while using the curvature information of the Hessian matrix to correct the search direction. In particular, when the Hessian matrix is positive, the update direction is bound to point to the local minima, while when it is not positive, the algorithm may converge to the saddle point or the maxima, which requires the regularization of the Hessian matrix or the use of the trust domain strategy in practical applications [7].

3.2. Vector Weighted Average Algorithm

XGBoost is an efficient and powerful integrated learning algorithm based on the gradient boosting framework, which improves model performance by combining multiple weak learners (usually decision trees) [8].The objective function of XGBoost consists of a loss function and a regularization term: the loss function measures the deviation of the predicted value from the true value; and the regularization term (L1/L2 regularization) controls the model complexity to prevent overfitting. Specifically, the regularization term consists of the L2 paradigm of the leaf node weights and the number of leaves in the tree, penalizing the complex tree structure. In the optimization process, XGBoost adopts a second-order Taylor expansion to approximate the loss function and updates the model using first-order gradient (G) and second-order gradient (H) information. Compared with the traditional GBDT using only the first-order derivatives, the second-order approximation can more accurately determine the direction and step size of the parameter update and improve the convergence efficiency. XGBoost constructs the tree structure by splitting the nodes layer by layer through the greedy algorithm [9]. The splitting gain is calculated as the difference between the loss reduction after splitting and the regularization penalty:

\( Gain=\frac{G_{L}^{¬}}{{H_{L}}+λ}+\frac{G_{R}^{¬}}{{H_{R}}+λ}-\frac{{({G_{L}}+{G_{R}})^{¬}}}{{H_{L}}+{H_{R}}+λ}-γ \)

where G and H are the sum of the gradient and second-order gradient of the left and right child nodes, respectively, and λ and γ are hyperparameters controlling the weight smoothing and splitting threshold, respectively. If the gain is greater than zero, it splits, otherwise it stops growing, thus balancing the model accuracy and complexity.

XGBoost can automatically handle missing values [10]. When finding the optimal splitting point, the algorithm calculates the gain of the missing values attributed to the left or right subtree respectively, and chooses the side with greater gain as the default direction. This dynamic processing mechanism eliminates the need to pre-populate the missing values and improves data adaptation.

Although Boosting itself is a serial spanning tree, XGBoost optimizes computational efficiency by pre-sorting (Block structure) with feature parallelization. Data is sorted by features and stored as blocks, and split-point computations for different features can be executed in parallel, while cache optimization reduces the overhead of repeated data access.

3.3. XGBoost optimized based on Newton-Raphson algorithm

Newton-Raphson Algorithm OptimizationThe core principle of XGBoost is to improve the traditional first-order optimization method of gradient boosting by introducing second-order derivative information, thus accelerating the convergence and improving the model accuracy. XGBoost adopts the second-order Taylor expansion in the optimization of the objective function, which approximates the loss function as a linear combination of the first-order gradient of the current model prediction (the direction of gradient descent) and the second-order Hessian matrix ( curvature information) as a linear combination to minimize the objective function more accurately. Specifically, in each iteration, XGBoost constructs statistics in terms of leaf nodes (e.g., the sum of the gradient and the sum of the Hessian) by calculating the gradient (first-order derivatives) and the Hessian (second-order derivatives) of the loss function for each sample, and calculates the splitting gain based on these statistics so as to select the optimal splitting point in the process of generating the tree structure. At the same time, the weight updates of the leaf nodes are derived from Newton's method, i.e., the weights, and the step size is adjusted by the second-order information so that the parameter updates are closer to the point of the minimal value of the loss function. This optimization strategy incorporating second-order information not only improves the model convergence speed, but also enhances the accuracy of split-point evaluation through the carving of local curvature by Hessian matrix, and effectively balances the model complexity and fitting ability by combining with the regularization term, which ultimately achieves a more efficient and accurate model training under the premise of guaranteeing generalizability.

4. Result

For parameter settings, the learning rate is set to 0.1, the maximum tree depth is set to 6, the minimum child node weight is set to 5, the sample sampling ratio is set to 0.8, the feature sampling ratio is set to 0.8, the L2 regularization coefficient is set to 1.0, the L1 regularization coefficient is set to 0.5, and the number of weak learners is set to 200. in terms of hardware configurations, we use a 16-core CPU, a 64GB RAM, a NVIDIA A100 graphics card. CUDA 11.6 driver acceleration, XGBoost 1.7.0 library, Python 3.9 interpreter.

Decision tree, random forest, XGBoost, CatBoost and our proposed Newton-Raphson algorithm to optimize the XGBoost algorithm are introduced for training respectively, and three experiments are averaged, and the model effectiveness is evaluated using accuracy, recall, precision, F1 score and AUC, and the results are shown in Table 2.

Table 2: Part of the dataset.

The output of the confusion matrix of our model predictions is shown in Figure 1. From the confusion matrix, we can see that a total of 21 predictions in the test set are correct, by 3 predictions are wrong, and the prediction accuracy is 87.5%.

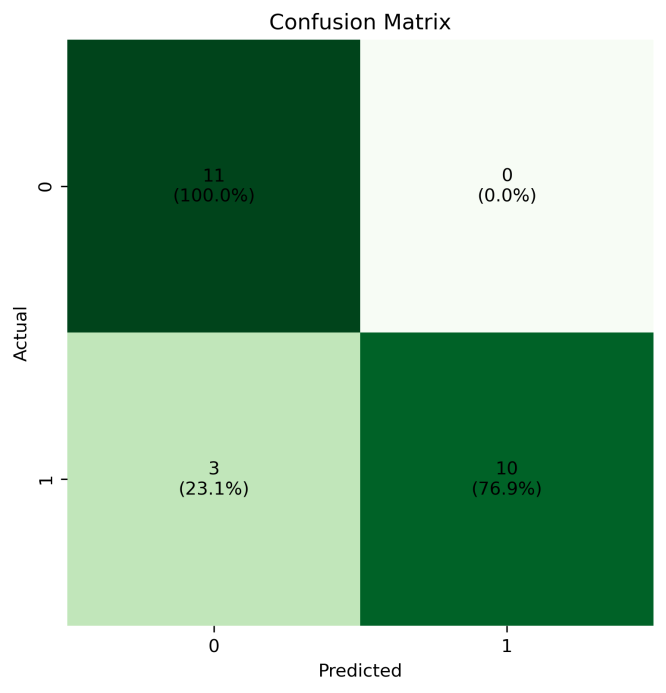
Figure 1: Confusion matrix for the test set.

The results of the comparison of the evaluation indicators for each model are shown in Figure 2.

Figure 2: The results of the comparison of the evaluation indicators for each model.

The accuracy and recall of Our model (both 0.875) are significantly higher than the other models, indicating that its overall prediction ability and recognition of positive class samples are stronger. It is worth noting that the accuracy and recall of Random Forest and XGBoost are both 0.792, but there is a difference in their precision and AUC, which may be due to the difference in feature selection or integration strategies. The accuracy and recall of Our model (both 0.875) are significantly higher than the other models, indicating that its overall prediction ability and recognition of positive class samples are stronger. It is worth noting that the accuracy and recall of Random Forest and XGBoost are both 0.792, but there is a difference in the precision and AUC between them, which may stem from the difference in feature selection or integration strategies.

5. Conclusion

The accuracy and recall of Our model (both 0.875) are significantly higher than the other models, indicating that its overall prediction ability and recognition of positive class samples are stronger. It is worth noting that the accuracy and recall of Random Forest and XGBoost are both 0.792, but there is a difference in their precision and AUC, which may be due to the difference in feature selection or integration strategies. The accuracy and recall of Our model (both 0.875) are significantly higher than the other models, indicating that its overall prediction ability and recognition of positive class samples are stronger. It is worth noting that the accuracy and recall of Random Forest and XGBoost are both 0.792, but there is a difference in the precision and AUC between them, which may stem from the difference in feature selection or integration strategies.

In this study, we improve and innovate the gradient boosting framework based on the classical optimization algorithm, propose the XGBoost optimization model (NR-XGBoost) integrating the Newton-Raphson algorithm, and apply it to the healthcare data analysis scenario of kidney stone risk prediction. In order to comprehensively verify the effectiveness of the improved model, the experimental session systematically constructed a comparison model system including traditional decision tree (CART), Random Forest, standard XGBoost, and the new integrated algorithm CatBoost. The empirical results show that the NR-XGBoost model proposed in this study achieves a significant advantage of 0.875 in the two core metrics of Accuracy and Recall, which is 10.5% higher than the other comparative models, demonstrating a better overall prediction performance and the ability to recognize positive class samples. Particularly noteworthy is that although the accuracy (0.792) and recall (0.792) of Random Forest and the standard XGBoost model perform exactly the same, there are differential fluctuations of 0.024-0.031 in the Precision and the area under the ROC curve (AUC) of the two, which may originate from both the differential partitioning of the feature space by the base-learner strategy, and may also be closely related to the algorithmic specificity of the strategies such as sample sampling and feature subspace construction during the integration process.

The conclusions of this study can be summarized at three levels: at the technical level, it is confirmed that the fusion of second-order optimization algorithms and integrated learning can effectively improve the predictive performance of medical data analysis; at the methodological level, the constructed NR-XGBoost model provides a new technological pathway for processing high-dimensional medical data; and at the application level, the developed renal stone risk assessment system has the potential for clinical translation. Future research will focus on the validation of the model's generalization ability on cross-medical organization data and the development of real-time dynamic prediction system, so as to promote the in-depth application of AI technology in the field of precision medicine.