1. Introduction
In recent years, the advancement of aviation automation has driven a trend toward crew reduction in aircraft cockpits, making Single-Pilot Operation (SPO) a research hotspot. In SPO, pilots shift from team-based to independent decision-making, intensifying the impact of component reachability and cockpit visual information on cognitive load. Previous studies have found that during the approach phase, the peak cognitive load in single-pilot flight can reach 0.7—well above the optimal range of 0.3–0.5[1]—thus threatening decision-making efficiency.
While some scholars have proposed a "pilot-centered" interface dynamic allocation principle [2], there remains a lack of multi-objective optimization methods that integrate spatial layout, visual information, and cognitive load. Therefore, this paper addresses three core issues:
Problem 1: How to analyze and optimize the reachability of pilot operations to ensure that key controls are accessible to pilots of various body sizes.
Problem 2: How to analyze and optimize cockpit color visibility by examining the effects of color selection and contrast on visual perception and information acquisition.
Problem 3: How to construct a multi-objective optimization model based on NSGA-II to balance reachability ( \( D \) ), contrast ( \( C \) ) and cognitive load ( \( L \) ), and validate the optimization under different weight configurations (e.g., wide-body versus narrow-body aircraft).
NSGA-II, proposed by Deb et al. in 2002[3], effectively balances convergence and diversity in multi-objective problems. The design in this study applies NSGA-II to generate a uniformly distributed Pareto front without preset weight biases, providing quantitative decision support for cockpit design.
2. Analysis on pilot operation behavior and cockpit color information design
2.1. Reachability analysis of pilot operation behavior
In a single-pilot environment, the pilot must operate multiple components within a limited space. Research by Ye et al. [4,5] indicates that cockpit design should account for the pilot’s body shape, operating habits, and task requirements. Yang [6] also noted that toggle switch errors are closely related to component reachability.
Reachability Design Based on Pilot Arm Length
Using the pilot’s sitting center as the origin, the Euclidean distance between an operating component and the origin is calculated as [7]:
\( d=√{({x_{comp}}-{x_{pilot}})^{2}}+{({y_{comp}}-{y_{pilot}})^{2}} \) (1)
If \( d≤Arm Length \) , the component is easily reachable; otherwise, layout adjustments or compensatory design measures are required.
Calculation of Reachability Score
Distance is converted into a reachability score \( D \) using formulas such as:
\( D=\frac{1}{1+d} \) or \( D=max(0, 1-\frac{d}{Arm Length}) \) (2)
A higher \( D \) signifies that the operating component is more accessible.
2.2. Analysis of visibility and cognitive load in cockpit color information design
Impact of Color Selection on Cognitive Load
Color plays a vital role in cockpit design by affecting information recognition and cognitive load. Li[8] recommends using high-saturation colors in interfaces emphasizing contrast to efficiently recognize hues such as red and yellow are preferable.
Impact of Contrast on Cognitive Load
Contrast is defined as the brightness ratio of a white screen (at its brightest) to a black screen (at its darkest) in a dark environment. A high-contrast design enables quick information identification and reduces cognitive load. However, excessively high or low contrast increases interpretation effort. Studies by Shen et al. [9] and Kang et al. [10] emphasize that optimized contrast is crucial for both safety and efficiency.
Calculation of Contrast Score
According to visual ergonomics theory, contrast \( C \) is calculated as:
\( C=\frac{{L_{max}}-{L_{min}}}{{L_{max}}+{L_{min}}} \) (3)
where \( {L_{max}} \) and \( {L_{min}} \) denote the maximum and minimum brightness levels, respectively.
3. Construction of multi-objective optimization model based on NSGA-II
This section describes parametric modeling, coding scheme, and optimization function construction for cockpit design. All parameters are mapped to the \( [0, 1] \) interval through normalization.
3.1. Parametric modeling and coding scheme
To comprehensively describe cockpit design elements, a parameter system is established comprising three main parts:
Spatial Layout: Position of operating components.
Visual Interface: Color contrast.
Mission Complexity: Workload for different flight phases.
A normalized coding strategy is used:
\( {X_{norm}}=\frac{X-{X_{min}}}{{X_{max}}-{X_{min}}} \) (4)
Where \( X \) is the original data. \( {X_{max}} \) , \( {X_{min}} \) are the maximum and minimum dataset values respectively.
3.1.1. Position of operating components
Using the pilot's sitting center as the origin \( (0, 0) \) , a coordinate system is based on the "Full Arm Length Parameters for Chinese Male Mixed Aircraft Pilots" (GJB 4856-2003):
Mean ± SE: 550.5 ± 0.52 mm
Standard deviation: 21.8 mm
Minimum: 487.0 mm, Maximum: 627.0 mm
The lateral range is set to \( [-62.7, 62.7] \) cm and the longitudinal range to \( [0, 62.7] \) cm. Four key operating components (main control stick, throttle lever, emergency button, and navigation panel) are linearly mapped using:
\( {x_{norm}}=\frac{x+62.7}{125.4} \) , \( {y_{norm}}=\frac{y}{62.7} \) (5)
3.1.2. Color contrast
Each of the four groups of operating components corresponds to brightness values \( {L_{max}} \) and \( {L_{min}} \) . Using the RGB color model (256 levels from 0 to 255), normalization is:
\( {L_{norm}}=\frac{L}{255} \) (6)
This converts the brightness values into a normalized value suitable for further processing.
3.1.3. Mission complexity
Mission complexity is quantified using NASA-TLX[11], which evaluates workload through six dimensions: mental demands, physical demands, temporal demands, performance, effort, and frustration. For each flight phase (takeoff, cruising, approach), pairwise comparisons yield relative importance scores \( {n_{i}} \) (with \( \sum _{i=1}^{6}{n_{i}}=15×k \) (7), constant \( k \) is normalized).
Weights are given by:
\( {w_{i}}=\frac{{n_{i}}}{15} \) (8)
Assuming raw scores \( {s_{i}} \) (ranging from 0 to 100) for each dimension, the weighted score \( {m_{i}} \) is computed as:
\( {m_{i}}=20{s_{i}} \) (9)
In this equation, the factor of 20 (derived from \( \frac{1}{5}×100 \) ) converts the raw score into a scale comparable with the normalized weights. The total workload for a flight phase is then calculated as:
\( Total Workload= \sum _{i=1}^{6}({m_{i}}×{w_{i}})=\sum _{i=1}^{6}(20{s_{i}}×\frac{{n_{i}}}{15})=\frac{20}{15}\sum _{i=1}^{6}({s_{i}}×{n_{i}}) \) (10)
These values are normalized to the \( [0, 1] \) range. Overall, 19 dimensions are encoded: 8 for operating components, 8 for color contrast, and 3 for mission complexity.
3.2. Construction of the multi-objective optimization function
The optimization function is defined as:
\( F={ω_{1}}∙D+{ω_{2}}∙C-{ω_{3}}∙L \) (11)
where:
\( F \) is the overall optimization score, a weighted sum of the three objectives.
\( D \) is the reachability score.
\( C \) is the color contrast score.
\( L \) is the pilot’s cognitive load.
\( {ω_{1}} \) , \( {ω_{2}} \) and \( {ω_{3}} \) are weight coefficients for each objective, satisfying \( {ω_{1}}+{ω_{2}}+{ω_{3}}=1 \) .
The negative sign before \( L \) indicates that reducing load is desired.
3.3. Analysis of weight distribution and aircraft model differences
Cockpit layout varies between wide-body and narrow-body aircraft, influencing weight distribution of the objectives, particularly the reachability score \( D \) .
3.3.1. Wide-body aircraft
Larger cockpits with widely distributed controls often force pilots to adjust posture or extend arms, leading to lower reachability scores \( D \) and a reduced \( {ω_{1}} \) . Consequently, higher weights are assigned to color contrast ( \( {ω_{2}} \) ) and cognitive load ( \( {ω_{3}} \) ). In this study, the weights for wide-body aircraft are set as:
\( {ω_{1}}=0.3,{ω_{2}}=0.35,{ω_{3}}=0.35 \)
3.3.2. Narrow-body aircraft
More compact layouts yield higher reachability scores, thus a higher \( {ω_{1}} \) , while \( {ω_{2}} \) and \( {ω_{3}} \) are lower. The weights for narrow-body aircraft are set as:
\( {ω_{1}}=0.5,{ω_{2}}=0.25,{ω_{3}}=0.25 \)
Simulations using these configurations generate two sets of Pareto front solutions via NSGA-II, revealing how changes in weight distribution affect trade-offs among \( D \) , \( C \) , and \( L \) .
3.4. NSGA-II algorithm process and simulation details
The NSGA-II algorithm is employed to address the multi-objective optimization problem, with the essential steps outlined as follows:
Population Initialization
An initial collection of solutions is created, and the values of their objective functions are computed.
Detail on Simulation Parameters: Population size = 200; mutation rate = 0.05; crossover rate = 0.8; iterations = 1000.
Non-Dominated Sorting
The population is segmented into several non-dominated fronts according to the principle of Pareto dominance.
Crowding Distance Calculation
For each solution, crowding distance is computed to ensure diversity. The formula is:
\( {crowding distance_{i}}=\sum _{m=1}^{M-1}\frac{{f_{m}}(i+1)-{f_{m}}(i-1)}{f_{m}^{max}-f_{m}^{min}} \) (12)
where \( {f_{m}}(i+1) \) and \( {f_{m}}(i-1) \) are the objective function values of the adjacent solutions, and \( f_{m}^{max} \) and \( f_{m}^{min} \) are the maximum and minimum values for the \( m-th \) objective respectively.
Selection, Crossover, and Mutation
A binary tournament selection is used to choose parent solutions. New solutions are generated via crossover and mutation.
Population Update and Iteration
The combined parent-offspring population is truncated back to the original size and repeated until a termination condition is met.
3.5. Experimental overview and results
Simulation experiments are conducted separately for wide-body and narrow-body aircraft using the specified weight configurations. The generated 3D Pareto fronts (Figures 1 and 2) demonstrate:
A uniform distribution in objective space, indicating effective exploration and diversity.
A trade-off between reachability and contrast: When reachability \( D \) is high, contrast \( C \) tends to decrease, suggesting that optimizing for accessibility might sacrifice visual clarity.
Lower contrast is associated with higher cognitive load, implying that suboptimal layouts force pilots to expend more cognitive resources. An increase in \( C \) can also lead to higher \( L \) due to potential visual interference.
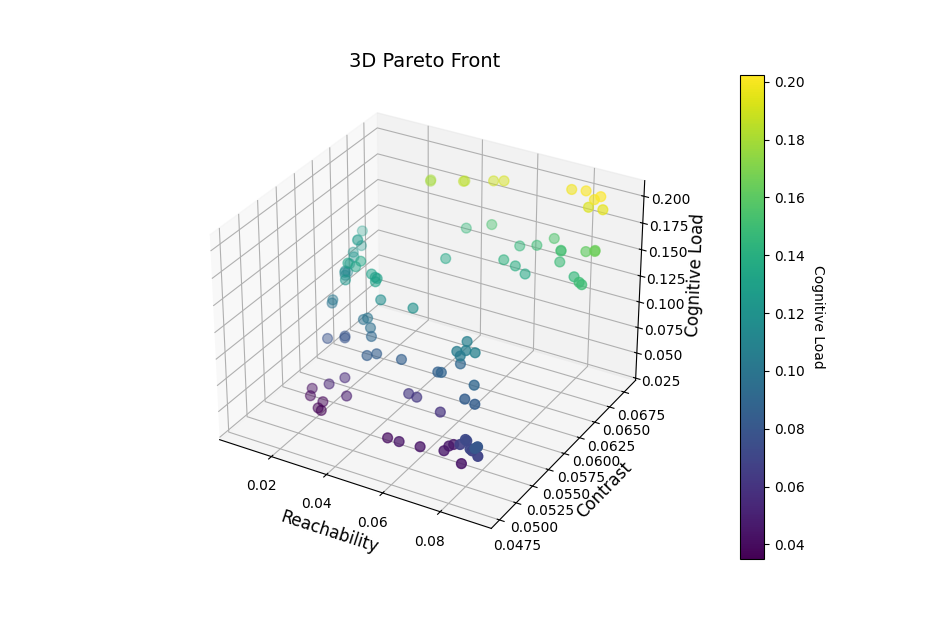
Figure 1: 3D Pareto front (wide-body aircraft)
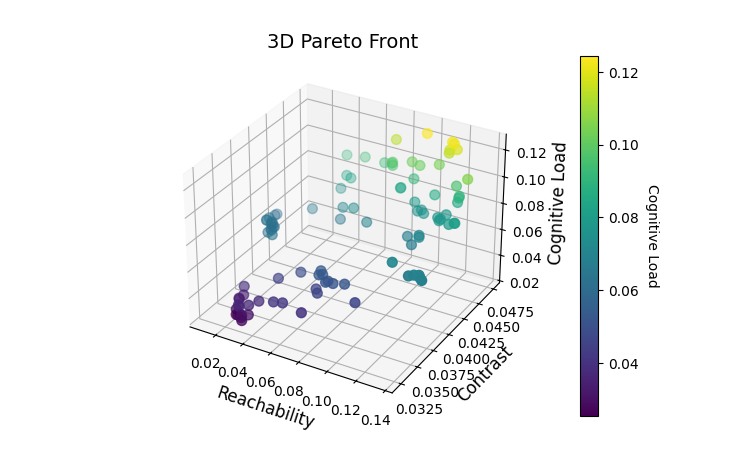
Figure 2: 3D Pareto front (narrow-body aircraft)
Comparative analysis reveals that wide-body aircraft solutions have lower \( D \) (due to a lower \( {ω_{1}} \) ), while narrow-body solutions exhibit higher \( D \) and more balanced \( C \) and \( L \) distributions.
4. Conclusion
This study explores the optimization of human-machine interaction in single-pilot aircraft cockpits, focusing on reachability, contrast, and cognitive load. By constructing a multi-objective optimization model based on NSGA-II, a three-dimensional evaluation system is developed to address complex design challenges. Simulation data—derived from theoretical assumptions and literature on pilot characteristics, component layouts, color contrast limits, and mission complexity—supports the study. The results reveal a complex trade-off among the three objectives, as illustrated by the Pareto front. The NSGA-II model effectively generates Pareto front solutions, providing a scientific basis for decision-making and assisting designers in selecting optimal cockpit configurations. This approach enhances cockpit interface usability and adheres to the "pilot as the core" principle, creating a more intuitive and less burdensome operating environment.
Despite its contributions, the study has certain limitations. The simulation relies on assumptions due to constraints in real-world data collection, which may introduce biases. Future work should incorporate empirical data from actual single-pilot flight environments to validate and refine the model. Additionally, this study simulated only daytime color contrast; future research should explore night-time conditions. Expanding the literature review and examining sensitivity to model parameters will further enhance the robustness of the findings.
Overall, this research establishes a systematic framework for optimizing cockpit layouts by balancing reachability, contrast, and cognitive load. Future research should verify and extend these findings with diverse datasets and explore additional factors and more efficient optimization algorithms to continually improve cockpit usability and safety.
References
[1]. Zhang, T., Shi, T., & Wei, Z. (2021). Adaptive adjustment method for automation level in single-crew operation. Chinese Journal of Safety Science, (08), 155–164.
[2]. Xu, W. (2022). Seven perspectives on user-centered design: From automation to intelligent aircraft cockpits. Applied Psychology, (04), 291–313.
[3]. Deb, K., Pratap, A., Agarwal, S., & Meyarivan, T. (2002). A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 6(2), 182–197.
[4]. Ye, K., Luo, T., Yang, W., Bai, Y., & Song, M. (2022). Optimization design of aircraft cockpit layout under multiple constraints. Human Ergonomics, (05), 84–87.
[5]. Ye, K., & Wei, S. (2017). Aircraft cockpit layout optimization design based on genetic algorithm. Journal of Armament and Equipment Engineering, (03), 108–110.
[6]. Yang, Y. (2023). A study on the factors affecting operating errors of cockpit toggle switches [Master’s thesis, Civil Aviation University of China].
[7]. Li, X. (2024). Analysis and optimization of general aircraft cockpit human-machine ergonomics based on motion characteristics [Master’s thesis, Civil Aviation Flight University of China].
[8]. Li, J. (2020). Digital interface visualization design and its cognitive load study in aircraft cockpits [Master’s thesis, Nanjing University of Aeronautics and Astronautics].
[9]. Shen, Z., Chen, G., Tu, W., et al. (2024). Human-computer interaction interface design of flight simulator based on situation awareness. Scientific Reports, 14, 27842.
[10]. Kang, N., Wang, S., Wang, Y., Wang, X., & Wang, J. (2024). Interface layout optimization algorithm based on intelligent optimization and multi-criteria decision model. Intelligent Computers and Applications, (09), 26–33.
[11]. Styler, B. K., Deng, W., Simmons, R., Admoni, H., Cooper, R., & Ding, D. (2024, March). Exploring control authority preferences in robotic arm assistance for power wheelchair users. In Actuators (Vol. 13, No. 3, p. 104). MDPI.
Cite this article
Zhou,Y. (2025). Research on the Optimization Design of Human-Machine Interaction in Single-Pilot Aircraft Cockpits. Theoretical and Natural Science,109,1-7.
Data availability
The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.
Disclaimer/Publisher's Note
The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
About volume
Volume title: Proceedings of CONF-MPCS 2025 Symposium: Leveraging EVs and Machine Learning for Sustainable Energy Demand Management
© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and
conditions of the Creative Commons Attribution (CC BY) license. Authors who
publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons
Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this
series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published
version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial
publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and
during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See
Open access policy for details).
References
[1]. Zhang, T., Shi, T., & Wei, Z. (2021). Adaptive adjustment method for automation level in single-crew operation. Chinese Journal of Safety Science, (08), 155–164.
[2]. Xu, W. (2022). Seven perspectives on user-centered design: From automation to intelligent aircraft cockpits. Applied Psychology, (04), 291–313.
[3]. Deb, K., Pratap, A., Agarwal, S., & Meyarivan, T. (2002). A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 6(2), 182–197.
[4]. Ye, K., Luo, T., Yang, W., Bai, Y., & Song, M. (2022). Optimization design of aircraft cockpit layout under multiple constraints. Human Ergonomics, (05), 84–87.
[5]. Ye, K., & Wei, S. (2017). Aircraft cockpit layout optimization design based on genetic algorithm. Journal of Armament and Equipment Engineering, (03), 108–110.
[6]. Yang, Y. (2023). A study on the factors affecting operating errors of cockpit toggle switches [Master’s thesis, Civil Aviation University of China].
[7]. Li, X. (2024). Analysis and optimization of general aircraft cockpit human-machine ergonomics based on motion characteristics [Master’s thesis, Civil Aviation Flight University of China].
[8]. Li, J. (2020). Digital interface visualization design and its cognitive load study in aircraft cockpits [Master’s thesis, Nanjing University of Aeronautics and Astronautics].
[9]. Shen, Z., Chen, G., Tu, W., et al. (2024). Human-computer interaction interface design of flight simulator based on situation awareness. Scientific Reports, 14, 27842.
[10]. Kang, N., Wang, S., Wang, Y., Wang, X., & Wang, J. (2024). Interface layout optimization algorithm based on intelligent optimization and multi-criteria decision model. Intelligent Computers and Applications, (09), 26–33.
[11]. Styler, B. K., Deng, W., Simmons, R., Admoni, H., Cooper, R., & Ding, D. (2024, March). Exploring control authority preferences in robotic arm assistance for power wheelchair users. In Actuators (Vol. 13, No. 3, p. 104). MDPI.









