1. Introduction

In the era of information saturation, personalized recommendation systems have become important tools across digital platforms. Whether in e-commerce, video streaming, or online news distribution, these systems play a vital role in helping users navigate vast content spaces and boost user engagement and platform profitability. The key algorithmic challenge, balancing exploration and exploitation, is to discover potentially relevant new content (exploration) while leveraging known user preferences (exploitation). It is difficult to manage especially under some environments, such as data sparsity, shifting user interests, and frequent cold-start conditions.

To address this problem, CMAB algorithms are powerful and adaptive frameworks. Unlike traditional multi-armed bandits, which treat all decisions in isolation, contextual multi-armed bandits (CMABs) adopt a different approach. They incorporate contextual features, such as user demographics and item attributes, into the decision-making process. It enables personalized real-time recommendations that adapt as more user interaction data become available. CMABs offer an online learning paradigm that is well-suited to the demands of modern recommendation systems, where models must be continuously updated in response to dynamic user behavior and partial feedback (e.g., clicks, likes or ratings).

Over the last decade, various CMAB algorithms have been proposed based on different theoretical principles. Explore-Then-Commit (ETC) algorithms first collect exploratory data, and then commit to an empirically optimal option. Although they often incur high initial regret because of the simple structure, they are still useful in some specific problem. In contrast, Upper Confidence Bound (UCB) algorithms follow the principle of "optimism in the face of uncertainty," offering strong theoretical guarantees and faster convergence in structured environments.And Thompson Sampling (TS) adopts a Bayesian perspective and probabilistically samples arms in proportion to their likelihood of being optimal, thus balancing exploration and exploitation.

Building on these foundational approaches, recent variants have improved adaptability to complex real-world scenarios. The Feel-Good Thompson Sampling (FG-TS) integrates an optimism bias into the TS framework to counteract sparse or adversarial feedback. Multinomial Logit UCB (MNL-UCB) extends UCB strategies to multinomial logistic regression models, which better represent discrete choice behavior typical in user selection scenarios. These advances have enabled CMAB algorithms to handle high-dimensional contexts and noisy or non-stationary environments more effectively.

Despite these theoretical developments, the practical performance of CMAB algorithms remains inconsistent across tasks and datasets. Many existing studies emphasize theoretical regret bounds or synthetic benchmarks, whereas real-world empirical evaluations are limited. Crucially, trade-offs among key concerns such as regret minimization, computational cost, algorithmic stability, and cold-start adaptability have yet to be systematically investigated within a unified, reproducible framework.

To bridge this gap, this study conducts a rigorous empirical comparison of three state-of-the-art CMAB algorithms: Double Explore-Then-Commit (DETC), FG-TS, and MNL-UCB. Experiments were performed on the widely used MovieLens 1M dataset, which contains rich user profile information and extensive interaction data for thousands of movies. The diversity and realism of this dataset make it an ideal testbed for evaluating contextual bandit algorithms under both short-term (200 rounds) and long-term (10,000 rounds) interaction scenarios.

This study has three core objectives. First, it develops a realistic contextual simulation framework that combines one-hot-encoded user attributes with low-dimensional movie embeddings generated via truncated singular value decomposition (SVD) and uses a logistic regression model to simulate probabilistic reward feedback. Second, it conducts a comprehensive quantitative assessment of algorithmic performance by measuring cumulative regret across short- and long-term interaction horizons. Third, it offers a preliminary examination of the strengths, limitations, and deployment tradeoffs of each algorithm. The goal is to provide useful insights for academic researchers and industry practitioners when considering CMAB strategies for recommendation systems.

2. Literature review

In the last few years, a lot of progress has been made in creating CMAB algorithms based on the basic ideas behind ETC, UCB, and TS. By using contextual information, these algorithms do a great job of balancing exploration and exploitation. They make big improvements in both the theoretical regret bounds and the empirical performance in a wide range of settings. Beygelzimer et al. were the first to add context to the ETC framework and create an adaptive exploration strategy with supervised learning guarantees [1]. They were the first to do this. At the same time, Chu et al. came up with LinUCB, which assumes a linear relationship between context and reward and chooses actions based on upper confidence intervals [2]. Around the same time, Slivkins suggested a similarity-based contextual bandit method that uses similarity metrics to adaptively divide the context space in order to improve performance in difficult situations [3].

There have also been big theoretical advances in UCB-based contextual bandit methods. Agrawal and Goyal added linear contextual settings to the UCB and found almost the best regret bounds [4]. Later, Li et al. expanded these findings to generalized linear bandits (GLBs), adding nonlinear link functions and creating algorithms that are provably optimal with strict guarantees [5]. Agarwal et al. came up with ILOVETOCONBANDITS, a sampling-based algorithm that optimizes policy distributions over arbitrary function classes [6]. This was done to solve computational problems while keeping statistical efficiency. Zhou et al. built on this work to create NeuralUCB, which uses deep neural networks to model complex nonlinear contexts and random feature mappings to create confidence bounds. The results were very good in practice and backed up by theory [7].

TS has also been a big part of research on contextual bandits. Riquelme et al. came up with Deep Bayesian Bandits by combining variational inference with Bayesian neural networks. They showed that it worked well in a number of benchmark environments [8]. This was further developed by Zahavy and Mannor, who proposed Deep Neural Linear Bandits, which mitigate catastrophic forgetting by combining deep feature extraction with Bayesian linear models on the output layer [9]. In order to align frequentist regret bounds with their Bayesian counterparts, even in adversarial environments, Zhang developed FG-TS, which incorporates an optimism bias [10].

Structural and parametric complexities of contextual bandits have been addressed by recent studies. Uehara et al. explored representation learning in low-rank Markov Decision Processes (MDPs) and proposed REP-UCB to enhance sample and computational efficiency in both online and offline reinforcement learning [11]. In the same year, Amani and Thrampoulidis developed the MNL-UCB, extending UCB strategies to multinomial logistic regression bandits, effectively addressing multi-class discrete feedback while maintaining sublinear regret [12]. Meanwhile, the ETC paradigm has witnessed renewed interest; Jin et al. proposed the DETC and introduced a four-phase exploration-exploitation cycle that achieves asymptotically optimal regret in non-fully sequential settings for the first time [13]. Moreover, Whitehouse et al. revisited kernel and Gaussian Process (GP)-based models, demonstrating that GP-UCB with appropriate regularization attains sublinear regret in environments with polynomial eigenvalue decay, thus extending UCB methods to rich function spaces with theoretical robustness [14].

Collectively, these developments illustrate the evolution of CMAB algorithms from early linear models to sophisticated frameworks incorporating deep learning and kernel methods, demonstrating a rich interplay between theoretical advancements and practical algorithm design. However, despite significant theoretical progress, existing studies have largely focused on regret bounds or simulations under synthetic conditions, leaving a notable gap in empirical evaluations of real-world recommendation tasks. Specifically, comparative studies systematically examining the trade-offs between regret minimization, adaptability to contextual complexity, and computational efficiency across multiple algorithms are limited. Furthermore, the practical implications of algorithmic choices under different interaction horizons, such as short-term versus long-term user engagement, have not been sufficiently explored.

To address these gaps, this study provides a comprehensive empirical comparison of three representative CMAB algorithms—DETC, FG-TS, and MNL-UCB—using the widely adopted MovieLens 1M dataset. By integrating realistic contextual modeling, including user profile encoding and movie embeddings via truncated SVD, with a logistic regression-based reward simulator, we constructed a robust experimental framework that mirrors real-world recommendation environments. Through a systematic evaluation under both short- and long-term interaction scenarios, this study not only benchmarks algorithmic performance using cumulative regret but also highlights the strengths, weaknesses, and application trade-offs of each method.

3. Methods

This section presents the three contextual bandit algorithms employed in this study: DETC, FG-TS, and MNL-UCB. Each method is designed to balance the exploration-exploitation trade-off through distinct mathematical frameworks and inference strategies. We describe their theoretical basis, decision rules, and practical implications in recommendation systems. Table 1 briefly summarizes the differences between the three algorithms.

3.1. Double Explore-Then-Commit (DETC)

DETC is a two-stage algorithm that first explores each arm uniformly and then commits to the arm with the highest estimated mean reward. It is simple and computationally efficient, making it ideal for environments with stable reward distributions. However, it lacks adaptivity in dynamic contexts.

Mathematically, the estimated reward for arm a after nₑ exploration rounds is:

$$$ \mathrm{\mu }̂\mathrm{ₐ}\mathrm{ }=\mathrm{ }(1\mathrm{ }/\mathrm{ }\mathrm{n}\mathrm{ₑ})\mathrm{ }\sum \mathrm{ᵢ}₌₁\mathrm{ⁿ}\mathrm{ₑ}\mathrm{ }\mathrm{r}\mathrm{ₐ},\mathrm{ᵢ}$$$(1)

The selected arm is:

$$$ \mathrm{a}\ast \mathrm{ }=\mathrm{ }\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{ₐ}\mathrm{ }\mathrm{\mu }̂\mathrm{ₐ}$$$(2)

Pseudocode:

Input: Number of arms K, total horizon T,

exploration steps nₑ

for a = 1 to K: 

for i = 1 to nₑ: 

Pull arm a, observe reward r_{a,i} 

Compute μ̂ₐ = (1/nₑ) * sum r_{a,i}

Select a* = argmax μ̂ₐf

or t = K * nₑ + 1 to T: 

Pull arm a*

3.2. Feel-Good Thompson Sampling (FG-TS)

FG-TS is a Bayesian approach that uses posterior sampling to select arms. It introduces a scaling parameter β ∈ (0,1] to amplify uncertainty in the posterior variance, promoting optimistic exploration. This is particularly effective in sparse-feedback or cold-start settings.

Mathematically, the posterior of arm a is:

$$$ \mathrm{\theta }\mathrm{ₐ}\mathrm{ }~\mathrm{ }\mathrm{N}(\mathrm{\theta }̂\mathrm{ₐ},\mathrm{ }\mathrm{\Sigma }\mathrm{ₐ})$$$(3)

With feel-good scaling:

$$$ \mathrm{\theta }̃\mathrm{ₐ}\mathrm{ }~\mathrm{ }\mathrm{N}(\mathrm{\theta }̂\mathrm{ₐ},\mathrm{ }\mathrm{\Sigma }\mathrm{ₐ}\mathrm{ }/\mathrm{ }\mathrm{\beta })$$$(4)

The arm selected at round t is:

$$$ \mathrm{a}\mathrm{ₜ}\mathrm{ }=\mathrm{ }\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{ₐ}\mathrm{ }\mathrm{x}\mathrm{ₜ}\mathrm{ᵀ}\mathrm{ }\mathrm{\theta }̃\mathrm{ₐ}$$$(5)

With updates:

$$$ \mathrm{A}\mathrm{ₐ}\mathrm{ }\leftarrow \mathrm{ }\mathrm{A}\mathrm{ₐ}\mathrm{ }+\mathrm{ }\mathrm{x}\mathrm{ₜ}\mathrm{ }\mathrm{x}\mathrm{ₜ}\mathrm{ᵀ},$$$

$$ \mathrm{b}\mathrm{ₐ}\mathrm{ }\leftarrow \mathrm{ }\mathrm{b}\mathrm{ₐ}\mathrm{ }+\mathrm{ }\mathrm{r}\mathrm{ₜ}\mathrm{ }\mathrm{x}\mathrm{ₜ},$$(6)

$$$ \mathrm{\theta }̂\mathrm{ₐ}\mathrm{ }=\mathrm{ }\mathrm{A}\mathrm{ₐ}⁻¹\mathrm{ }\mathrm{b}\mathrm{ₐ}$$$

Pseudocode:

Input: Number of arms K, context dimension d, scaling parameter β

Initialize for each arm a:

 Aₐ = I_d, bₐ = 0_d

for t = 1 to T:

 Observe context xₜ

 for each arm a:

 Compute θ̂ₐ = Aₐ⁻¹ bₐ

 Σₐ = σ² Aₐ⁻¹

 Sample θ̃ₐ ~ N(θ̂ₐ, Σₐ / β)

 Compute score pₐ = xₜᵀ θ̃ₐ

 Select aₜ = argmaxₐ pₐ

 Pull arm aₜ and observe rₜ

 Update Aₐ and bₐ accordingly

3.3. Multinomial Logit Upper Confidence Bound (MNL-UCB)

MNL-UCB combines an upper confidence bound framework with a multinomial logit model. It uses both estimated utility and uncertainty to select arms and probabilistically models user choices. This approach performs well in environments with discrete choices and personalized rankings.

Mathematically, the choice probability is:

$$$ \mathrm{P}\left(\mathrm{a}\mathrm{ }\right|\mathrm{ }\mathrm{x}\mathrm{ₜ})\mathrm{ }=\mathrm{ }\mathrm{e}\mathrm{x}\mathrm{p}(\mathrm{x}\mathrm{ₜ}\mathrm{ᵀ}\mathrm{ }\mathrm{\theta }\mathrm{ₐ})\mathrm{ }/\mathrm{ }\sum \mathrm{ⱼ}\mathrm{ }\mathrm{e}\mathrm{x}\mathrm{p}(\mathrm{x}\mathrm{ₜ}\mathrm{ᵀ}\mathrm{ }\mathrm{\theta }\mathrm{ⱼ})$$$(7)

The UCB score for arm a is:

$$$ \mathrm{U}\mathrm{C}\mathrm{B}\mathrm{ₐ}\mathrm{ }=\mathrm{ }\mathrm{x}\mathrm{ₜ}\mathrm{ᵀ}\mathrm{ }\mathrm{\theta }̂\mathrm{ₐ}\mathrm{ }+\mathrm{ }\mathrm{\alpha }\mathrm{ }\surd (\mathrm{x}\mathrm{ₜ}\mathrm{ᵀ}\mathrm{ }\mathrm{V}\mathrm{ₐ}⁻¹\mathrm{ }\mathrm{x}\mathrm{ₜ})$$$(8)

With updates:

$$$ \mathrm{V}\mathrm{ₐ}\mathrm{ }\leftarrow \mathrm{ }\mathrm{V}\mathrm{ₐ}\mathrm{ }+\mathrm{ }\mathrm{x}\mathrm{ₜ}\mathrm{ }\mathrm{x}\mathrm{ₜ}\mathrm{ᵀ},$$$

$$$ \mathrm{b}\mathrm{ₐ}\mathrm{ }\leftarrow \mathrm{ }\mathrm{b}\mathrm{ₐ}\mathrm{ }+\mathrm{ }\mathrm{r}\mathrm{ₜ}\mathrm{ }\mathrm{x}\mathrm{ₜ},$$$(9)

$$$ \mathrm{\theta }̂\mathrm{ₐ}\mathrm{ }=\mathrm{ }\mathrm{V}\mathrm{ₐ}⁻¹\mathrm{ }\mathrm{b}\mathrm{ₐ}$$$

Pseudocode:

Input: Number of arms K, context dimension d, exploration parameter α

Initialize for each arm a: 

 Vₐ = I_d, bₐ = 0_d, θ̂ₐ = 0_d

for t = 1 to T:

 Observe context xₜ

 for each arm a:

 Compute UCBₐ = xₜᵀ θ̂ₐ + α 

√(xₜᵀ Vₐ⁻¹ xₜ)

 Select aₜ = argmaxₐ UCBₐ

 Pull arm aₜ, observe rₜ

 Update Vₐ, bₐ, θ̂ₐ

4. Experiment design

This chapter describes the experimental framework designed to evaluate the effectiveness of specific contextual multi-armed bandit (CMAB) algorithms in a controlled simulation environment. The experiment attempted to replicate realistic user-item interactions while maintaining methodological rigor and reproducibility by utilizing the MovieLens 1M dataset.

4.1. Data process

The MovieLens 1M dataset, which comprises approximately one million ratings from 6,000 users on 4,000 films, was used in the experiment. The contextual bandit environment was built using three data files: ratings.dat, users.dat, and movies.dat. To create user context vectors, one-hot encoding was used to create fixed-length representations of categorical user profile attributes, such as gender, age, and occupation. To capture collaborative signals among movies and facilitate efficient generalization within the contextual bandit framework, we built a user-movie rating matrix and used Truncated Singular Value Decomposition (SVD) to extract low-dimensional latent embeddings for movie features. To simulate user feedback, a binary classification reward model was built: each user-movie-rating triplet was labeled positive if the rating was 4 or higher. The final feature vector was formed by concatenating the one-hot encoded user vector with the movie embedding. A logistic regression model was trained on 80% of the data (using train_test_split), with the remaining 20% reserved for validation. During the simulation, this logistic regression model acts as a stochastic oracle, where the predicted probability of a user-movie pair serves as the success probability for Bernoulli reward generation.

4.2. Parameters setting

The key parameter settings of the experiment are outlined below, along with the rationale for each choice, which aims to ensure both practical realism and methodological clarity.

Contextual Feature Dimensions: User features were encoded via one-hot encoding of gender (two categories), age group (seven bins), and occupation (21 roles), resulting in a 30-dimensional user context vector. Movie features are represented using a 20-dimensional latent embedding obtained from the truncated SVD on the user-movie rating matrix. By concatenating the user and movie vectors, each interaction context forms a 50-dimensional feature vector. This setup strikes a balance between expressive power and computational efficiency, capturing the interactions between user preferences and movie content representations.

Simulator Configuration: The candidate arms consisted of 10 randomly selected movies chosen to maintain experimental control while keeping the computational cost manageable. All users from the dataset were included to simulate both cold-start and warm-start conditions. Reward feedback is generated using Bernoulli sampling based on the predicted click probabilities from the trained reward model, thereby mimicking the binary feedback (click vs. no click) commonly observed in real-world recommendation systems while also introducing realistic noise.

Bandit Algorithm Settings:

DETC: In a setting with only 10 arms, the exploration phase is set up with five rounds per arm, which guarantees a sufficient number of initial observations to support trustworthy commitment decisions while limiting the exploration overhead.

FG-TS: TS is implemented using Gaussian priors with added covariance regularization, enabling approximate posterior sampling in high-dimensional contexts while maintaining numerical stability.

MNL-UCB: A moderate degree of optimism was indicated by the confidence bound scaling parameter, which was set to α = 1.0. This prevents unduly drastic departures from the estimated means and encourages a fair trade-off between exploration and exploitation of the data.

Simulation Configuration: Each algorithm was run for 10,000 rounds to evaluate its long-term performance. To reduce the impact of stochastic variance, each configuration was repeated over 10 independent trials. The mean and standard deviation of cumulative regret across trials were then computed for analysis. This design ensures both robustness and computational feasibility, facilitating a reliable comparison among the algorithms.

In summary, the parameter settings were carefully chosen to reflect practical recommendation scenarios while maintaining consistency and reproducibility across experiments. They support the fair evaluation of exploration-exploitation trade-offs in complex contextual conditions.

4.3. Experimental procedures

The experiment is conducted according to the following steps:

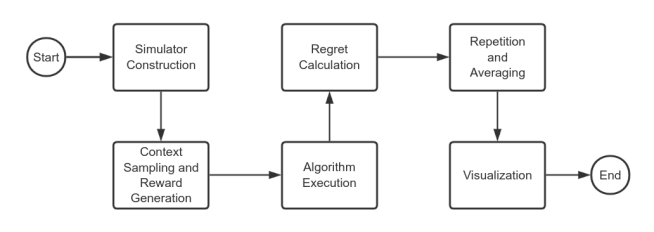
As the Figure1, the Experimental flow chart, shows that first, a simulator is constructed using the trained reward model. At each interaction round, a user is uniformly sampled from the user set. The context is then formed by combining the one-hot encoded profile of the selected user with the embeddings of the candidate movies.

For each round, the simulator evaluates all candidate movie arms by computing the predicted probability of receiving a positive reward under the current context. A Bernoulli reward is then sampled for each arm based on its predicted probability, thereby simulating the user’s click behavior.

For each contextual bandit algorithm, the following loop is executed: the algorithm selects an arm based on the current context, observes the corresponding reward, and updates its internal estimates or posterior distribution accordingly. The instantaneous regret at each round is defined as the difference between the highest predicted reward probability and the probability of the selected arm. These values are accumulated to compute the cumulative regret over time.

To account for stochastic variability, each experiment is independently repeated 10 times. The mean and standard deviation of cumulative regret are then calculated. The results are visualized by plotting cumulative regret trajectories with shaded confidence intervals, enabling a comparative evaluation of algorithmic performance across rounds.

5. Result ＆ discuss

This chapter provides a systematic evaluation of three CMAB algorithms—DETC, FG-TS, and MNL-UCB—on the MovieLens dataset for recommendation tasks. The experiments were designed under two settings: long-term (10, 000 rounds) and short-term (200 rounds) interactions. The primary performance metric is cumulative regret, which reflects the gap between the chosen and optimal actions in each round.

Figure 2 illustrates the cumulative regret curves for long-term interaction scenarios. The results show that DETC performs reasonably well in the early rounds but experiences a rapid increase in regret as the number of interactions increases, eventually exceeding 1200. Moreover, its wide confidence interval indicates high instability in the trials. FG-TS outperforms DETC by maintaining a cumulative regret of approximately 800, with a smooth curve and moderate growth rate, reflecting better convergence and stability. MNL-UCB achieves the lowest regret across all rounds, stabilizes below 600, and exhibits the narrowest confidence band, demonstrating strong robustness and consistency.

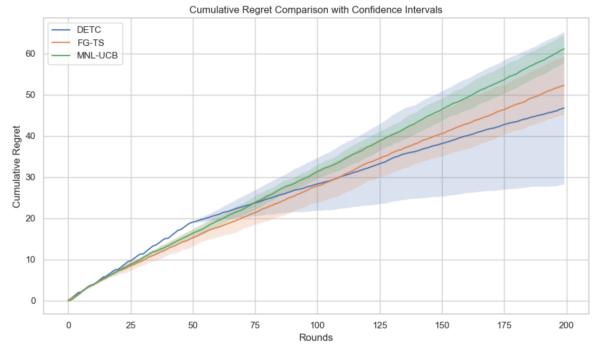
Figure 3 presents the results of the short-term recommendation scenario of 200 rounds. During the first 50 rounds, the regret of all three algorithms increased linearly and remained comparable. However, performance differences became evident in the later stages. The DETC accumulated regret rapidly during exploration, followed by slower growth, achieving the best performance with a final regret of approximately 50. FG-TS maintained a constant regret growth. It performed slightly worse than DETC but still better than MNL-UCB. However, MNL-UCB showed the highest cumulative regret, which was completely different from the long-term results.

Further analysis revealed that the exploration-exploitation strategy is the key determinant of performance. The DETC follows a hard-switching approach by conducting a fixed number of initial explorations before committing fully to the estimated best arm. While this can work under ideal conditions, such as large differences in true arm expectations and low early estimation error, in practice, the complexity of contextual features and noisy feedback may lead to misidentification of the optimal arm early on, resulting in persistent regret accumulation. This highlights that fixed exploration phases are ill-suited for real-world systems, and that soft switching or gradual commitment strategies may be more appropriate.

In contrast, Bayesian posterior sampling helps the FG-TS balance exploration and exploitation in each round. An arm may be assigned a high-sampled value when its level of uncertainty is high, which promotes exploration. However, fewer samples were obtained from arms with low uncertainty. Owing to this mechanism, FG-TS can effectively adjust to contextual drift, sparse data, and cold-start users, making it especially effective in dynamic environments.

The MNL-UCB conducts a confidence-bound approach which is comparable to the optimistic exploration of classical machine learning. It favors understudied and promising arms in the selection process of the best-performing arms. This mechanism provides strong robustness and fast convergence, and performs well under structured environments with stable and interpretable contexts. However, it might converge too soon to less-than-ideal solutions in the early stages or when the data are skewed.

Runtime efficiency and implementation complexity must be considered when deploying a system. The DETC is appropriate for situations with stringent latency constraints because it has the simplest structure and the lowest computational cost. In contrast, matrix updates and sampling or inversion operations are used in FG-TS and MNL-UCB, which could lead to performance snags in large-scale systems. By giving uncertain arms priority and quickly adjusting to new users or items, FG-TS naturally excels at solving cold-start issues. MNL-UCB is better suited for established systems with established patterns than MNL because it has fewer parameters, is easier to tune, and has better interpretability.

The current implementation of reward modeling makes use of logistic regression, which is straightforward and easy to understand but might not have the necessary expressive power. Nonlinear and higher-order interactions frequently control click behavior in the real world. To more accurately predict user behavior, future research should take into account using nonlinear models, such as generalized additive models (GAMs) or multi-layer perceptrons (MLPs). Furthermore, the current model does not explicitly model user-item interaction effects; instead, it simply concatenates user features and movie SVD embeddings. The simulator's realism could be improved by using sophisticated architectures like factorization machines, attention-based models, or neural interaction layers.

In summary, the MNL-UCB performs best in the long run and works well with systems that are stable and well-structured. In dynamic and unpredictable environments, FG-TS performs exceptionally well, particularly in cold-start or short-term scenarios. Despite its computational efficiency, DETC has stability issues in intricate situations. By weighing theoretical guarantees, system requirements, and practical performance, these findings provide useful suggestions for selecting suitable contextual bandit algorithms for real-world recommendation systems.

6. Conclusion

Using the MovieLens 1M dataset, we conducted a thorough empirical evaluation of three representative CMAB algorithms: DETC, FG-TS, and MNL-UCB. The evaluation was conducted in a realistic recommendation environment. Cumulative regret was used as the main performance metric in the experiments conducted under both short-term (200 rounds) and long-term (10,000 rounds) interaction horizons. According to the results, MNL-UCB is best suited to structured, stable environments because it continuously achieves the lowest cumulative regret and shows high stability. Through Bayesian posterior sampling, FG-TS demonstrated a robust performance in dynamic or uncertain scenarios, quickly adjusting to new users or items. Although DETC is computationally efficient, its rigid exploration strategy makes it less robust in complex or noisy contexts. These findings highlight the critical trade-offs between simplicity, adaptability, and statistical efficiency in real-world CMAB deployments. Additionally, this study contributes a reproducible experimental framework that integrates user profiles and movie embeddings into a logistic reward model, offering practical suggestions for algorithm benchmarking and selection in future studies.

Despite these contributions, several limitations of this study must be acknowledged. The assumption of a static context and a fixed item pool does not reflect the dynamic, feedback-driven nature of real-world systems. Future studies should incorporate context drift and temporal feedback to improve realism. The restricted arm set (10 movies) limits the scalability evaluation; expanding to thousands of items would better mirror industrial-scale recommendation settings. Furthermore, the current reward model relies on logistic regression, which may oversimplify user-item interactions by failing to capture nonlinear or higher-order dependencies. Evaluation metrics are also limited to cumulative regret, omitting business-relevant indicators such as the click-through rate (CTR), coverage, diversity, and ranking quality (e.g., NDCG, MAP). Future research should explore more expressive reward models (e.g., neural networks or attention-based architectures), simulate realistic user dynamics, scale up candidate pools, and incorporate broader evaluation metrics to support more holistic and actionable assessments of the proposed method. In summary, this study offers both empirical insights and methodological tools for advancing CMAB research and informing real-world recommendation system design.