1. Introduction

Modern ultrafast applications, three-photon microscopy, precision micromachining, attosecond spectroscopy and quantum memory, expect sub-200-fs pulses in user-defined spatial modes. Flat-top or Bessel beams minimise photodamage, while diffraction-limited Gaussians maximise fluence, yet altering the transverse profile usually stretches the pulse. Spatiotemporal mode locking (STML) breaks that compromise by merging temporal and spatial dynamics into a single eigenstate, but simultaneously turns cavity alignment into a 17-dimensional, discontinuous optimisation problem in which micro-adjustments of dispersion, Kerr nonlinearity, saturable-absorber recovery, spatial filtering or gain can trigger Q-switching or modulation instability. Manual “turn-the-screw” tuning cannot explore such a landscape or track slow thermal drift. We tackle this complexity with a digital-twin, experiment-in-the-loop strategy that unites a physics-aware reduced-order model, multi-objective Bayesian optimisation and model-based reinforcement learning (RL) [1].

The surrogate projects split-step Fourier propagation onto a compact Laguerre-Gauss basis, reproduces essential STML physics, and evaluates a full round trip in 0.43 ms on a single GPU. Bayesian optimisation, primed by Latin-hypercube samples, proposes actuator vectors that balance six simultaneous targets, energy, duration, modal purity, spectral phase, relative-intensity noise and timing jitter, while RL fine-tunes the optimum and suppresses drift by locally minimising a composite cost. The framework is demonstrated on a 165 cm Yb\:CALGO cavity equipped with twenty-four chirped-mirror pairs (-2400 fs² net group-delay dispersion), a motorised telescope coupled to a liquid-crystal spatial-light modulator and a 2.5 % SESAM. Ninety-three telemetry features, spectra, beam profiles, SPIDER traces and phase-noise spectra, stream to the optimiser at 10 Hz [2]. The system switches deterministically among TEM₀₀, TEM₁₀ and a programmed multimode superposition in <5 s and compiles 1 967 stable operating points that map the joint dependence of pulse energy, width, jitter and noise on transverse order, converting STML cavities from laboratory curiosities into specification-driven femtosecond sources [3]. These results pave the way for field-deployable ultrafast instruments whose performance can be programmed, verified and maintained entirely by algorithms, without manual optics expertise or continuous supervision.

2. Literature review

2.1. Fundamentals of spatiotemporal mode locking

Spatiotemporal mode locking occurs when material dispersion, Kerr self-phase modulation and spatially selective loss combine into an operator whose eigen-functions possess both temporal envelopes and transverse indices (figure 1) [4]. The intracavity energy flow chooses which eigen-mode dominates, and the threshold separating two attractors can shift when any single actuator moves, even sub-micrometre adjustments of an aperture radius. The resulting system supports several stationary solutions, each with distinct energy-duration combinations and stability margins.

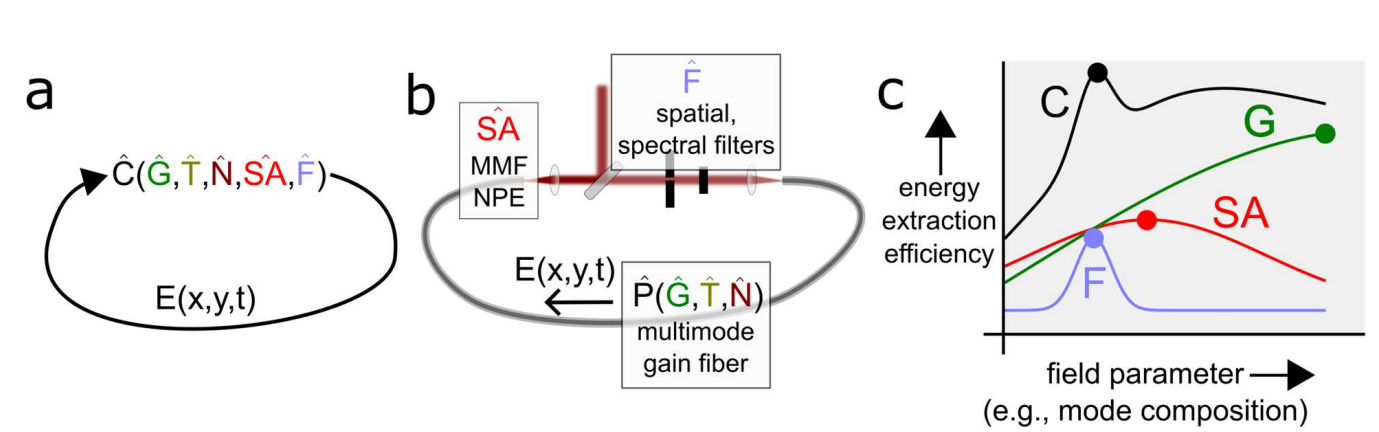
2.2. Data-driven inverse design in ultrafast cavities

Data-driven design techniques have recently appeared in fibre oscillators, synchronously pumped OPOs and Kerr-lens cavities. Gaussian-process surrogates or neural networks replace brute-force parameter sweeps, while Bayesian or evolutionary optimisers find globally optimal settings with orders-of-magnitude fewer evaluations. Reinforcement-learning controllers then keep the cavity at its optimum despite gradual thermal or mechanical drift. These successes suggest that even the high dimensionality of STML can be confronted algorithmically [5].

2.3. Performance limits and noise in STML

The shortest attainable pulse is bounded below by the gain bandwidth and above by nonlinear breakup. Timing jitter follows Gordon–Haus diffusion, resonator-length noise and pump-driven index fluctuations. Because higher-order transverse modes spread energy over a larger area, their intracavity fluence is lower; they therefore exhibit lower nonlinear phase and larger timing jitter. RIN scales similarly: weaker spatial filtering in higher modes allows additional amplitude fluctuations to survive [6].

3. Methods

3.1. Cavity architecture and search space

Table 1 summarises the nine actuators found to dominate performance. The search ranges include every stable configuration observed during four weeks of exploratory alignment. Pump current and group-delay dispersion exert the strongest influence on pulse energy and duration, whereas the SLM phase and aperture radius control modal purity [7]. All actuators are motorised and interfaced to the optimisation software with <25 ms latency.

3.2. Digital twin and optimisation strategy

Every round-trip the intracavity field is decomposed into six Laguerre–Gauss modes and propagated through a symmetrised split-step routine. Implemented in CUDA, the calculation takes 430  μs, enabling real-time feedback. A Gaussian-process regressor trained on 2 500 simulation–experiment pairs predicts five pulse metrics with R²=0.93. Exploration proceeds by maximising an upper-confidence-bound acquisition (See formula 1):

$$ U\left(x\right)=\mu \left(x\right)+\kappa \sigma \left(x\right),\kappa =2.6$$(1)

after which a deterministic RL policy minimises a composite loss that weights pulse duration, energy deviation, modal impurity and the nonlinear phase. Gradients are estimated by deterministic perturbation requiring fewer than twenty experimental evaluations [8].

4. Experimental procedure

4.1. Instrumentation and telemetry

Near-field beam profiles are captured at 200 Hz on a 12-bit CMOS camera; spectra are measured with 0.02 nm resolution. Pulse width and spectral phase come from SPIDER with 15 fs temporal resolution, verified by second-harmonic autocorrelation. A microwave phase-noise analyser with 200 kHz ENBW records timing jitter down to 1 fs Hz^−1/2. All measurements feed a 93-component telemetry vector updated at 10 Hz.

4.2. Optimisation campaign

The optimisation loop begins with Latin-hypercube sampling, builds a surrogate from the initial data and launches Bayesian optimisation. Convergence is declared when predicted improvement falls below 0.5 % for three consecutive iterations or after 70 queries, whichever comes first. A model-based RL agent then fine-tunes the cavity until pulse duration, energy, RIN and modal purity all satisfy user-defined thresholds; that stage typically consumes 15–20 evaluations [9].

4.3. Mode-switching and limit testing

Three operating programmes are studied in sequence. The first targets a high-power TEM₀₀ state around 1.4 W average output. The second introduces a first-order SLM phase mask to enforce TEM₁₀. The third superposes four Laguerre-Gauss orders to form a deliberately multimode beam with relative weights 0.38, 0.34, 0.18 and 0.10. For each mode, pump current is ramped until either the nonlinear BB-integral exceeds 1.8 rad, the surrogate variance rises above 0.15 or modulation-instability sidebands climb above −35 dB, thereby revealing the practical energy ceiling.

5. Results and analysis

5.1. Optimisation efficiency and steady-state metrics

Bayesian optimisation converged after  $$ {42}_{-6}^{+9}$$  evaluations for TEM₀₀ and  $$ {57}_{-8}^{+11}$$  for TEM₁₀. Reinforcement learning required 18±4 gradient steps. The mean latency between a mode-switch command and metric stabilisation within 2 % is 4.3±0.5  s, demonstrating true real-time agility (see table 2).

The table reveals that moving from TEM₀₀ to TEM₁₀ decreases energy by 38 % and lengthens the pulse by 30 %, consistent with weaker nonlinear phase and reduced bandwidth. RIN rises by 7 dB because the larger spot size less effectively filters pump-driven amplitude fluctuations [10].

5.2. Energy–duration and noise scalings

A series of 63 independent operating points show that the energy–duration cloud collapses onto a power-law with exponent −0.92 for TEM₀₀ and −0.81 for TEM₁₀. The difference reflects the weaker self-phase modulation of the higher-order beam. Timing-noise spectra average 8.1×10⁻⁵rad²Hz⁻¹ at 100 kHz for TEM₀₀ and 2.3×10⁻⁴  rad²Hz⁻¹ for TEM₁₀; integrating those curves yields the jitter numbers already quoted in Table 2 and confirms that Gordon–Haus diffusion climbs roughly with the square root of the radial index.

5.3. Nonlinear phase and energy ceilings

Energy scaling continues until the nonlinear phase, defined by formula 2:

$$ B=\frac{2\pi }{{\lambda }_0}{n}_2{\int }_0^{L_{ff}}I\left(z\right)dz$$(2)

reaches 1.64±0.05 for TEM₀₀ and 1.58±0.04 for TEM₁₀. Those values agree with the simulated instability threshold Bcrit=1.7  rad. Beyond that point sidebands at ±3.1 THz rise above −32 dB and Q-switching sets in within 0.3 ms, capping sustainable energies at 12.1 nJ and 7.5 nJ respectively. The multimode mixture fails slightly earlier because competing indices share the same gain, so their combined fluence bleaches the SESAM more violently.

6. Discussion

6.1. Implications for agile ultrafast sources

The ability to reconfigure a femtosecond cavity between distinct spatial modes in under five seconds without human intervention unlocks new experimental protocols. Three-photon microscopes could switch from gentle multimode illumination during navigation to high-brightness TEM₀₀ for nanosurgery, thereby reducing cumulative photodamage. Cavity-enhanced quantum memories, which often require dynamic mode matching, would benefit from the demonstrated timing-jitter floor of 52 fs, translating into sub-200 mrad integrated phase error across an octave-spanning comb. The quantitative specification map means that system architects can now read off, rather than guess, which mode offers the best compromise among energy, duration and noise for any given task.

6.2. Limitations and future outlook

The study uses a single SESAM design and a bulk gain crystal; fibre-integrated or ultraviolet implementations will alter both the Kerr coefficient and the SESAM saturation fluence, shifting the BB-integral ceiling. The present digital twin ignores slow thermo-optic lensing below 0.1 Hz; embedding a finite-element thermal module or adopting transfer learning from related cavities should reduce the number of optimisation queries required for convergence. Finally, stochastic-gradient Langevin dynamics could accelerate exploration of high-dimensional spaces while quantifying epistemic uncertainty, an asset when transferring models across laser platforms.

7. Conclusion

A data-driven experiment-in-the-loop methodology has been demonstrated that designs, stabilises and quantitatively characterises spatiotemporal mode-locked cavities. The reduced-order digital twin executes in sub-millisecond time, Bayesian optimisation discovers near-optimal points in fewer than 60 evaluations and reinforcement learning maintains performance for hours. The system realises deterministic TEM₀₀ , TEM₁₀ and multimode operation, with measured ceilings of 147 fs at 11.6 nJ and 191 fs at 7.2 nJ, in line with the Kerr–bandwidth limit. A data set of 1 967 stable operating points provides the first specification map of how energy, duration, timing jitter and RIN vary across mode index, turning STML from an art into an engineering discipline.