1. Introduction

Quantum mechanics is a branch of physics. It deals mainly with microscopic matters together with relativity, which is considered one of the two fundamental pillars of modern physics. Many physical theories, such as solid state physics, nuclear physics and particle physics, and other related disciplines, are based on it. Quantum mechanics also led to the creation of many interdisciplinary fields, such as quantum biology and quantum thermodynamics, that are being explored today. Today, it is worth mentioning that too little work has been devoted to the combination of different interdisciplinary applications with the conception of quantum mechanics. However, this plays a pivotal role in understanding what next step will the researchers take. The overall structure of the paper takes the form of four chapters. Firstly, this author introduces the development of quantum mechanics and expresses its own views. Secondly, the authors explain how quantum mechanics foreshadows transistors and lasers. Thirdly, on the basis of the existing research results of quantum computing and quantum biology, the author summarizes the previous views on these two fields. Finally, the author gives his own views on the current research of quantum mechanics and the future development of interdisciplinary subjects.

2. Introduction of quantum mechanics

Born at the turn of the 20th century and in its full form in the mid-1920s, quantum mechanics is the mathematics that explains matter. It is a revolution of classical physics in the microscopic field, where atoms and molecules interact to generate the world of human experience. It's at the heart of everything that makes this century so different from the century that came before it. From cell phones to supercomputers, quantum physics fueled the present-day electronics-based economy, transforming commerce, communication and entertainment[1].

The central idea of quantum theory is that everything consists of unpredictable particles, but the statistical behavior of these particles follows a predictable pattern of fluctuations.

The German physicist Heisenberg discovered that the microscopic world has an endogenous and quantifiable uncertainty. He envisaged the use of a gamma-ray microscope to observe the coordinates of an electron, because the gamma-ray microscope's ability to split the office is limited by the wavelength, the shorter the wavelength of the light used into the higher the resolution of the microscope, thus determining the degree of uncertainty in the coordinates of the electron is smaller, so \( ∆x∝λ \) . But on the other hand, light irradiation to the electron can be seen as a collision of light quanta and electrons, the shorter the wavelength, the momentum of the light quanta is increasingly large, so \( ∆p∝1/p \) . After some reasoning and calculations, Heisenberg concluded that \( ∆x∆p≥h/4π \) . Therefore, momentum and coordinates cannot be measured accurately at the same time.

In addition to the uncertainty principle, quantum mechanics has many other characteristics, such as quantum non-locality and coherence, which have led many physicists to make related research. However, the correctness of a theory must be tested by experiments. The study of quantum mechanics needs to be inherited and developed critically.

3. Development of quantum mechanics

3.1. The origin of quantum mechanics

The limitation of classical mechanics makes quantum mechanics come into being. In order words, many phenomena of experiments cannot be explained by existing theories at that time. For example, faced with the problem of black-body radiation, scientists developed the Rayleigh-Jeans formula law, which is based on classical physics. It is found that the energy density of black-body radiation rises with the radiation frequency and tends to infinity. But this is not consistent with the experimental data. This is a famous ultra-violet catastrophe. There are similar instances such as the stability of an atom, emission spectrum and photoelectric effect which both can not be explained by classical physics.

3.2. Old quantum theory

3.2.1 Planck's law. Faced with the ultraviolet disaster, Planck suddenly had an inspiration one day. He subtracted one from the denominator of Venn's formula to get Planck's law. Plank’s law tends to the Venn formula in the high-frequency region and the Rayleigh-Kings formula in the low-frequency region. Planck's law is in good agreement with the experiment:

\( u(λ,T)=\frac{8πhc}{{λ^{5}}}∙\frac{1}{{e^{\frac{hc}{λkT}}}−1} \) (1)

On December 14, 1900, Planck presented the physical implications of Planck's formula at the German Physical Society in Berlin. That is, Planck's formula can be derived by introducing the concept of quantization of oscillator energy. Planck broke through the concept of energy as continuous in classical physics and introduced quantum, the smallest unit of energy, thus giving birth to quantum mechanics. Therefore, December 14, 1900 is generally regarded as the "birth date" of quantum mechanics.

3.2.2 The photoelectric effect. When light strikes a metal surface, it causes electrons to be ejected, causing the photoelectric effect. If this metal is connected to a wire, the wire will produce an electric current.(see Figure 1). What's interesting is that when the beam is less than a certain frequency, no matter how strong the beam is, it can't eke out electrons; Only when the frequency of the light is higher than that will there be electron spillover. This frequency is called the critical frequency.

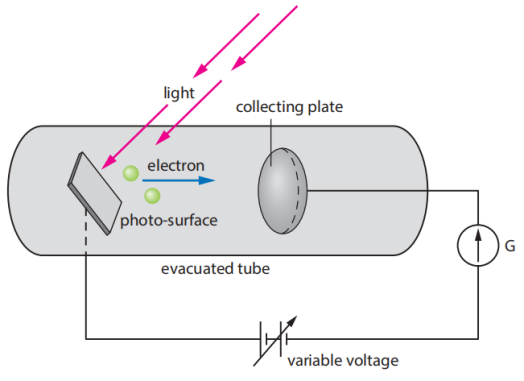
Figure 1. Apparatus for investigating the photoelectric effect[2].

In a 1905 paper, Einstein postulated that light itself consists of localized particles (quanta). He explained the photoelectric effect perfectly and won the 1921 Nobel Prize in Physics for his explanation of the photoelectric effect.

3.2.3 Atomic structure. As people learn more about the composition of matter, they find that the atom is not the smallest unit of matter. When proving matter, Thomson model transferred into Rutherford model. The Rutherford model was a great advance in understanding atomic structure, but it had a fatal problem. According to Maxwell's equations, an accelerating electron orbiting an atomic nucleus must radiate electromagnetic waves, lose energy, and eventually collide with the nucleus. As a result, the atomic structure will eventually collapse and not remain stable.

So in 1913, Bohr revised the model. He posited that the position of the electron in the atom was not arbitrary, but that it moved in certain orbits, where it did not radiate electromagnetic waves, and that it emitted or absorbed electromagnetic waves only when it moved from one orbit to another. Bohr's model of the atom explains the Balmer formula well:

\( v=R(\frac{1}{{2^{2}}}−\frac{1}{{n^{2}}}) n=3,4,5,... \) (2)

But Bohr's model of the atom, which does not explain why electrons move in certain orbitals and why energy is quantized, does not start from the most basic theory, lacks theoretical support; And Bohr's model could not account for the motion of more than two electrons. Nevertheless, Bohr's model inspired countless subsequent physicists, including Heisenberg and Schrodinger, to study atomic models from a quantized perspective and eventually establish the theory of quantum mechanics. Bohr's model of the atom was, so to speak, a bridge to the theory of quantum mechanics.

3.3. The establishment of quantum mechanics

3.3.1 Heisenberg matrix mechanics. In 1924, at the age of 23, Heisenberg went on an academic visit to the Copenhagen Institute. By then he had completed his PhD in Gottingen, Germany, under the supervision of Born. Heisenberg's visit to Copenhagen had a profound influence on his creation of the matrix mechanical form of quantum mechanics. In 1925, he returned to Gottingen to continue his studies. Heisenberg believed that physical research should be based on observable measurements, while in Bohr's atomic model, the orbits and frequencies of electrons were not observable. What is observable are the frequencies, intensities, polarizations, and energy orders of the spectral lines that are frequently exposed. So he started with observable quantities and abandoned the idea of electron orbitals. While finally recuperating on a secluded island, Heisenberg developed a new theory of quantum mechanics called Heisenberg matrix mechanics. In 1925, his article was published in the Journal of Physics. In matrix mechanics, every physical quantity is represented by a matrix. It is based on Hamiltonian mechanics and retains the functional relations of various mechanical quantities, but the multiplication of matrices does not satisfy the commutative law of multiplication. This property is also known as "incommutability". Heisenberg matrix mechanics is a natural way of deriving the energy levels and radiation frequencies of atoms.

In 1924, at the age of 23, Heisenberg went on an academic visit to the Copenhagen Institute. By then he had completed his PhD in Gottingen, Germany, under the supervision of Born. Heisenberg's visit to Copenhagen had a profound influence on his creation of the matrix mechanical form of quantum mechanics. In 1925, he returned to Gottingen to continue his studies. Heisenberg believed that physical research should be based on observable measurements, while in Bohr's atomic model, the orbits and frequencies of electrons were not observable. What is observable are the frequencies, intensities, polarizations, and energy orders of the spectral lines that are frequently exposed. So he started with observable quantities and abandoned the idea of electron orbitals. While finally recuperating on a secluded island, Heisenberg developed a new theory of quantum mechanics called Heisenberg matrix mechanics. In 1925, his article was published in the Journal of Physics. In matrix mechanics, every physical quantity is represented by a matrix. It is based on Hamiltonian mechanics and retains the functional relations of various mechanical quantities, but the multiplication of matrices does not satisfy the commutative law of multiplication. This property is also known as "incommutability". Heisenberg matrix mechanics is a natural way of deriving the energy levels and radiation frequencies of atoms.

3.3.2 Schrodinger wave mechanics. Schrodinger's wave mechanics also begins with wave-particle duality. The debate over whether light is a particle or a wave has been going on for a long time. The particle theory of light was established in Newton's time. With the stamp of Newton, the absolute authority of physics at the time, scientists at the time chose to believe that light was a particle. In 1801, Thomas Young placed two very close double slits between the light source and the screen, through which light formed interference fringes on the screen. Young's double slit interference experiment confirmed the phenomenon of light interference, but only wave interference can occur, wave theory is gradually accepted by people. It was not until 1905 when Einstein proposed the quantum of light and successfully explained the "photoelectric effect", that the particle nature of light was once again experimentally confirmed. In addition, in 1923, Compton, while studying the scattering problem, found that if you shine X-rays on graphite scatterers, some of the X-rays will be scattered by electrons, and their wavelength will be longer. The Compton effect is also a good example of particle property. Light has the wave-particle duality, which is the wave-particle duality of light, as well as the wave-particle duality of light. Not only light, but also matter such as electrons and atoms have wave-particle duality. Thus, inspired by Einstein's concept of light quantum, de Broglie proposed the concept of wave-particle duality in 1924. He pointed out that all matter in nature is both fluctuating and particle. If Heisenberg's matrix mechanics was inspired by Bohr's atomic model, Schrodinger's wave mechanics was inspired by wave-particle duality. Schrodinger regarded electrons as waves and derived a non-relativistic wave equation from classical mechanics. That is:

\( iħ\frac{∂φ}{∂t}=−\frac{{ħ^{2}}}{2m}{∇^{2}}φ+Vφ \) (3)

In quantum mechanics, particles are no longer described by equations of motion, but by wave functions. Schrodinger's paper was published in 1926. Since then, the wave equation form of quantum mechanics has been formally established. In April of the same year, Schrodinger proved that Heisenberg matrix mechanics and wave mechanics were mathematically equivalent.

4. Applications for quantum mechanics

Applications of quantum mechanics include the explanation of natural occurrences and the development of quantum-effects-based technology like integrated circuits and lasers. By directly displaying which molecules are energetically preferable to which ones and the magnitudes of the energies involved, quantum mechanics can also offer quantitative insight into the processes of ionic and covalent bonding. Quantum chemistry is the study of chemistry through the lens of quantum mechanics.

There are many technologies today that rely on quantum mechanics. Superconducting magnets, light-emitting diodes, optical amplifiers, lasers, transistors, semiconductors, microprocessors, magnetic resonance imaging, and electron microscopy are a few examples of important quantum theory applications. The part below will discuss two typical applications.

4.1. Transistors

The band theory of quantum mechanics well explains the performance principle of semiconductors between conductors and insulators and is the physical basis of transistor operation. Transistors are the basic building blocks of all kinds of chips. In 1947, William Shockley, John Bardeen, and Walter Brattain of Bell LABS created the first practical semiconductor device, the transistor(see Figure 2), based on knowledge of quantum theory. It can make the voltage change through it proportional to the change of the output current, so as to have detection, rectification, amplification, switching, voltage regulation, signal modulation and other functions. Transistors can also be made very small, gradually replacing the larger, slower response time vacuum tubes. It started the whole field of integrated circuits, which is now the field of microelectronics.

Figure 2. The first transistor ever made, built by John Bardeen, William Shockley and Walter H. Brattain of Bell Labs in 1947. Original exhibited in Bell Laboratories[3]

4.2. Laser

The theory of lasers dates back to Albert Einstein's further study of the photoelectric effect in 1917. He proposed that the interaction between light and matter consists of three processes: stimulated absorption, stimulated radiation and spontaneous radiation. In 1953, American physicist Charles H. Townes and his student American physicist Arthur L. Schawlow made the first microwave quantum amplifier based on this principle and obtained a highly coherent microwave beam. In 1958, Charles H. Townes and Arthur L. Schawlow extended the maser principle to the spectral segment, and put forward the concept of laser and the first theoretical scheme of laser. In 1960, Theodore H. Maiman, an American physicist, invented the first stimulated radiation amplification device of light, namely the laser. Laser light quality is a pure and stable spectrum that can be used widely, such as all kinds of information scanning, optical fiber communication, laser ranging, liDAR, laser records, etc. New applications are still being improved and popularized. Laser has become one of the most important light sources by virtue of its incomparable monochromatism and collimation.

5. Inter-discipline related to quantum mechanics

Today, we have entered the second era of quantum technology revolution, which is to develop quantum technology and applications through active artificial design and manipulation of quantum states. Quantum theory has been successfully derived from quantum communication, quantum cryptography, quantum computing, quantum optics and a series of cutting-edge interdisciplinary subjects. The development of these disciplines has great scientific significance and strategic value. Many new quantum technologies such as quantum computers can be seen as an impact on the traditional technology system. It may be a prelude to a new round of scientific and technological revolution and even industrial change.

5.1. Quantum computation.

A quantum computer is a machine that performs quantum computation. The concept of quantum computing and quantum computer originated from Feynman, a famous physicist, who proposed it in 1982 when he studied the use of classical computers to simulate quantum mechanical systems. In 1985, Deutsch proposed the model of the quantum Turing machine, and through the study of its properties, predicted the potential power of quantum computers. Because quantum computer relies on the law of quantum mechanics to process information, it has a huge advantage that classical computers will never be able to overcome. Quantum computers not only offer more bits and higher clock speeds, they also offer a new way of computing based on quantum algorithms.

5.1.1 Quantum bit. Classical information systems take a bit as the unit of information. A bit is a physical system with two states, which can be prepared as one of two recognizable states, such as yes or no, true or false, 0 or 1. In a digital computer, the voltage between the plates of a capacitor represents bits of information, with a charge representing a 1 and no charge representing a 0. In quantum information systems, quantum bits are commonly used to represent information units. Quantum computers use two-state quantum mechanical systems to describe two-position information, such as the two polarization directions of photons |↑|and │→|, the two directions of electron spin or nuclear spin up and down in magnetic fields, and the two energy states of electrons in atoms. The process of quantum computing by quantum computers is the evolution of the quantum states of these quantum mechanical systems.

Quantum bits differ from classical bits in that they can exist in a state that is neither one nor two, but can exist as a superposition of two logical states, i.e quantum state

\( |Ψ \) |= \( α|0|+β|1| (4), {|α|^{2}}+{|β|^{2}}=1(5) \) for example, \( |Ψ \) |= \( \frac{1}{\sqrt[]{2}}|0|−\frac{1}{\sqrt[]{2}}|1| \) (6)

The situation described here is not identical with a random bit having values {0,1} and probabilities \( {|α|^{2}} \) , \( {|β|^{2}} \) . Whereas a total of 4 different transformations can explain all possible transformations of a random bit, a quantum bit can be transformed in infinitely many ways. Rotations of a so-called Bloch sphere can be used to represent the various transformations that can be applied to a quantum bit.

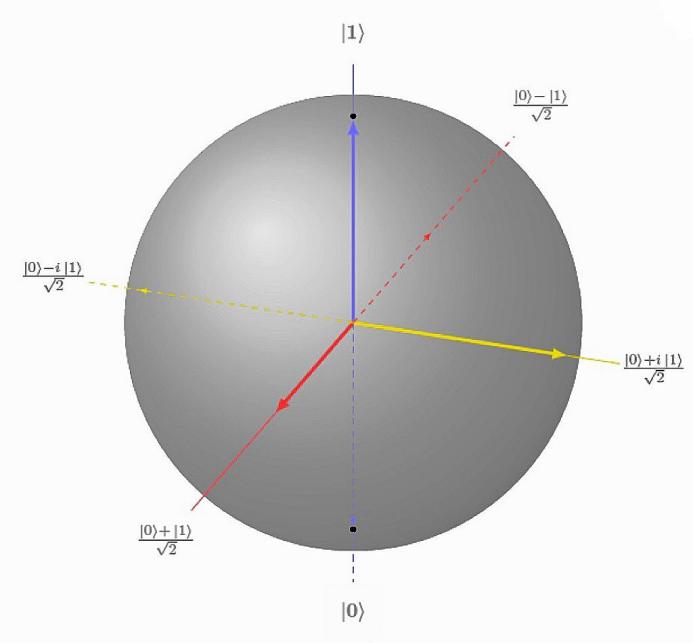
Figure 3. Bloch Sphere[4]

5.1.2 Quantum logic gate. The unitary development of encoded quantum states is the foundation of quantum information processing. The most fundamental unitary operations of quantum bits are quantum logic gates. Contrarily, quantum computing uses quantum logic gates to regulate and manage the evolution and transmission of quantum states in order to process quantum information. Consequently, the only prerequisite for a quantum logic gate is unitary property. A quantum logic gate can be described by any matrix that satisfies a unitary condition.

5.1.3 Quantum parallelism. The most significant benefit of quantum computers over traditional computers is quantum parallel computing. When it comes to processing specific tasks in parallel, quantum computers have an advantage over classical computers in terms of speed. A 2-bit classical register, for instance, may encode 22 distinct integers, including 00, 01, 10, and 11. One of them, however, can only be stored at a time. Quantum superposition enables the simultaneous storage of 22 numbers in a 2-bit quantum register, and a single quantum state can represent all the numbers. 23 distinct numbers can be stored simultaneously in a 3-qubit memory, and so on.For a tied quantum memory, it can store two different numbers (states) at the same time. In quantum mechanics, the general state of a register with N quantum bits can be expressed as

\( |Ψ|=\sum _{x=0}^{{2^{n}}}{c_{n|x|}}(7) \) [5]

Currently, simple quantum computers, which can have up to dozens of coupled quantum bits, can do about 100 gate operations before failing. John Preskill, a physicist at Caltech, refers to this process as "noisy intermediate-scale quantum computing." [6]

5.2. Quantum biology.

The study of applying quantum mechanics and theoretical chemistry to aspects of biology that cannot be adequately described by conventional physical laws is known as quantum biology[7].

The conversion of energy into forms that may be used for chemical reactions is a fundamental biological activity that is fundamentally quantum mechanical in nature. Chemical reactions themselves, light absorption, the creation of excited electronic states, the transfer of excitation energy, the transfer of electrons and protons, etc. are all examples of these processes. It has also been hypothesized that several other biological processes, such how birds fly in the Earth's magnetic field, depend on quantum mechanics[8].

5.2.1 Quantum mitochondrion. Mitochondria are the organs with the most active metabolism of substances and energy in life activities, and there are a lot more quantum effects in mitochondria than we imagined [9]. Among them, the research on quantum mechanics in the generation of free radicals (ROS), the electron transport chain (ETC) and the mitochondrial oscillator is the most useful research in understanding the existence of complex nonlinear mitochondrial system [10]. At the molecular level, the REDOX role of electron transport chains has been well elucidated by scientists through the colocalization of genes and gene products. From the perspective of quantum biology, mitochondria is a quantum control system, including quantum coherence, quantum penetration and quantum entanglement.

5.2.2 Quantum brain hypothesis. Existing research tentatively suggests that quantum mechanics dominates the brain's sensory outposts. For example, retinal photoreceptor cells containing rhodopsin are essential for the production of vision, and high-resolution spectroscopy and nuclear magnetic resonance technology have shown the presence of coherent quantum waves in rhodopsin molecules [11]. Quantum effects are also found in olfaction, and electron tunneling plays an important role in detecting material odors by olfactory receptors[12]. The quantum coherence and quantum entanglement effects in avian retinal cryptochrome can well explain the navigation induction of avian magnetic receptors[13]. The above research elucidated the existence of quantum effects in sensory cells, and the hypothesis about quantum brain needs to be further confirmed by experiments.

Figure 4. Using ultracold atoms and ions, superconducting junctions, and diamond defects to perform quantum computing in our own brains. [14]

6. Conclusion

This paper mainly discusses the development and application of quantum mechanics. We concluded that, today, there are a lot of things that quantum mechanics can't solve, but it's not that quantum mechanics itself has a theoretical flaw that needs to be perfected, it's the problem of how to use quantum mechanics, or how to unify quantum mechanics with other branches of physics. For example, attempts to unify quantum mechanics with general relativity, such as string theory, Grand Unified theory, quantum gravity. The mathematical advances in this direction are fascinating, but at the moment the physical possibilities are largely untestable and have few direct applications. In addition, with the continuous development of quantum mechanics, there are many interdisciplinary subjects derived from it, such as quantum thermodynamics, quantum computation, quantum communication and quantum biology. However, there is still much to be done on the frontier of these research. For instance, quantum communication and quantum computing have a wide range of application prospects. Although their fundamental structures have been established, numerous theoretical and technical issues still need to be resolved in order to realize quantum computing and communication that has some real-world applications. For example, how to find a suitable physical system to construct a quantum computer in the short term, how to efficiently generate entangled states of many particles, and which physical system is better for storing quantum information. We are confident that as theory and technology advance and more professionals and academics engage in quantum mechanics research, a variety of interdisciplinary domains will rapidly advance and play a significant role in advancing science, technology, and humankind in the future. Considering the logic of the whole article, some knowledge of quantum computing and quantum biology is not very comprehensive. Therefore, sometimes it is easy to make some researchers who are not very familiar with the related fields have certain confusion.