1. Introduction

1.1. Research background

Photons have multiple degrees of freedom, such as frequency, time, amplitude, phase, and polarization. By manipulating the different properties of the photons, structured beams with different characteristics can be obtained. In the past, the research on laser beams mainly focused on the power, time and spectral characteristics, and the research on the spatial characteristics of lasers was not deep enough. However, in the last ten to twenty years, the spatial characteristics of laser beams have received extensive attention and research.

Structured beams can be divided into spatial-structured light beams and spatiotemporal light beams. Spatially structured beams refer to the inhomogeneous distribution of the light field in space with parameters such as phase, intensity, and polarization. At the same time, the plane where the non-uniform distribution of the light field is located is perpendicular to the laser propagation direction. However, the light field distribution of spatiotemporal structured beams exists in both the space domain and the time domain.

Compared with the traditional Gaussian modes, the complex structured beams formed by the higher-order transverse modes can accommodate more modes, making it a prospective application in the fields of optical communication and quantum information [1]. At the same time, because some structured beams have the characteristics of orbital angular momentum, they are widely used in optical tweezers and atom manipulation [2]. In addition to the above applications, structured beams can also be used in light detection, quantum entanglement and other fields [3].

1.2. Research progress

The generation mechanism of spatially structured beams can be explained by the Maxwell-Bloch (MB) field theory or the eigenmodes superposition theory [4]. The MB equation (equation (1)) solves the distribution of the electric field on the plane perpendicular to the beam propagation (transverse plane) in the space and time domains based on the relationship between the electric field strength and the atomic polarization and the number of reversed particles, thus explaining the formation of structured beams [5].

\( \begin{cases} \begin{array}{c} \frac{∂E}{∂t}=-(i{ω_{c}}+κ)E+κP+idκ{∇^{2}}E \\ \frac{∂P}{∂t}=-{γ_{⊥}}P+{γ_{⊥}} \\ \frac{∂D}{∂t}=-{γ_{\prod [(D-{D_{0}})+\frac{1}{2}({E^{*}}P+{P^{*}}E)]}} \end{array} \end{cases}\ \ \ (1) \)

Where E is the electric field strength, P is the atomic polarization strength, D is the population inversion strength, κ, γ_⊥, γ_∏ are the decay rates, ω_c is the resonant frequency of the cavity, and d is the diffraction coefficient. It can be seen from the above equation that since there are three decay rate coefficients in the MB equation, by changing the relationship between the three decay coefficients, the Complex-Ginzburg-Landau (CGL) equation and the Complex-Swift-Hohenberg (CSH) equation are proposed. By manipulating the stimulated emission conditions of the laser, the spot shape and time-domain characteristics of different laser states are explained. The CGL equation (equation (2)) is obtained under the condition of γ_⊥ ≈ γ_∏ ≫ κ. According to the CGL equation, the transverse structured beam can be controlled by changing the length of the resonator [6]. The CSH equation (equation group (3)) is obtained under the condition of γ_⊥ ≫ γ_∏ ≈ κ [7].

\( \frac{∂E}{∂τ}=({D_{0}}-1)E-i(β-d{∇^{2}})R-g{(β-d{∇^{2}})^{2}}E-E{|E|^{2}}\ \ \ (2) \)

\( \begin{cases} \begin{array}{c} \frac{∂E}{∂τ}=(D-1)E-i(β-d{∇^{2}})R-g{(β-d{∇^{2}})^{2}}E \\ \frac{∂D}{∂τ}=-{γ_{\prod [(D-{D_{0}})+{|E|^{2}}D]}} \\ \end{array} \end{cases}\ \ \ (3) \)

One-dimensional and two-dimensional structured beams can be obtained by solving the MB equation, CGL equation and CSH equation. And the above equation can simultaneously explain the characteristics of beams with different spatial structures in time domain and space domain. However, the light spot of the spatially structured beam obtained by the above equation is mainly generated by a single transverse mode laser. For the light spot produced by multiple transverse modes and transverse modes with phase differences, it is difficult to explain through the above equation. Therefore, eigenmode superposition theory is proposed.

The laser transverse eigenmodes are obtained by solving the Helmholtz equation under different coordinate systems. Through the coherent and incoherent superposition of different eigenmodes, different structured beams can be obtained. Different from the MB equation field theory, the Helmholtz equation in the eigenmode superposition theory does not consider the time-domain characteristics of the beam. Based on the Gaussian beam, the Helmholtz equation can be solved in the Cartesian coordinate system and cylindrical coordinates, which leads to the Hermite-Gaussian mode (HG) and the Laguerre-Gaussian mode (LG) [8, 9]. At the same time, based on the HG mode, the LG mode is obtained by coherent superposition of HG, and the intermediate state Ince-Gaussian mode (IG) is obtained based on the LG and HG modes [10]. Bessel mode and Mathieu-Gauss mode can be obtained by combining the cylindrical coordinates and elliptic cylindrical coordinates of the Helmholtz equation in free space [11, 12]. At the same time, the Airy beam can be obtained by solving the paraxial wave equation [13]. By solving the Helmholtz equation in parabolic coordinates, a parabolic beam and a parabolic accelerated vector beam can be obtained [14, 15].

\( {E_{m,n}}=\sum _{m,n}{a_{m,n}}X{G_{m,n}}*exp{[i{ϕ_{m,n}}+ikz+ik\frac{{x^{2}}+{y^{2}}}{2R(z)}-iqѰ(z)]}\ \ \ (4) \)

Based on the eigenmodes obtained by solving the above Helmholtz equation in different coordinate systems and the Transverse Mode Locking (TML), coherent superposition between different transverse modes, the different structured beams can be obtained (as shown in equation (4)). Wang Xin et al. studied the structured beams generated by the coherent and incoherent superposition of the HG eigenmodes through the transverse mode locking effect [16].

1.3. Research content

In this paper, based on the eigenmode superposition theory, the formation mechanism of the structured beam is analyzed. The first three-orders of structured beams generated by the coherent superposition of the HG eigenmodes are given by numerical simulation. At the same time, by setting up the experimental system, the complexed structured beams were, and compared with the simulation results to prove the correctness of the eigenmode superposition theory.

2. Theoretical analysis

By solving the paraxial approximated Helmholtz equation in Cartesian coordinates, the HG mode is obtained:

\( {HG_{m,n}}(x,y,z)=\frac{C_{m,n}^{HG}}{{ω^{2}}(z)}exp(-\frac{{x^{2}}+{y^{2}}}{{ω^{2}}(z)}){H_{m}}(\frac{\sqrt[]{2}x}{ω(z)}){H_{m}}(\frac{\sqrt[]{2}y}{ω(z)}) \)

\( exp{[ikz+ik\frac{{x^{2}}+{y^{2}}}{2R(z)}-i(m+n+1)Ѱ(z)]}\ \ \ (5) \)

Where \( C_{m,n}^{HG} \) is a normalization factor, m and n are the horizontal and vertical mode numbers of the HG mode, and ω(z) is the half-width of the beam at the z position \( {ω^{2}}=ω_{0}^{2}({z^{2}}+z_{R}^{2})/z_{R}^{2} \) , ω₀ is the beam waist of the HG eigenmodes, Z_R is the Rayleigh range, Ѱ(z) is the Gouy phase, R(z) is the radius of curvature of the wavefront, H_m and H_n are Hermite polynomials.

By solving the paraxial approximated Helmholtz equation in cylindrical coordinates, the LG beam is obtained:

\( {LG_{p,l}}(r,ϕ,z)=\frac{C_{p,l}^{LG}}{ω(z)}{(\frac{\sqrt[]{2}r}{ω(z)})^{|l|}}exp(-\frac{{r^{2}}}{{ω^{2}}(z)})L_{p}^{|l|}(\frac{{r^{2}}}{{ω^{2}}(z)}) \)

\( exp{(ilϕ)}exp{[ikz+ik\frac{{r^{2}}}{2R(z)}-i(2p+|l|+1)Ѱ(z)]}\ \ \ (6) \)

Where \( C_{p,l}^{LG} \) is the normalization factor, p and l are the radial and angular indices of the LG mode, which respectively determine the radius and number of the ring structure of the LG beam, and \( L_{p}^{|l|} \) is the generalized Laguerre polynomial.

Taking HG as an example, this paper obtains the structured beams by coherent superposition of HG eigenmodes. First, taking the coherent superposition of two modes as an example, as shown in equation (7):

\( E(x,y,z)={α_{1}}{HG_{1}}exp{(i{φ_{1}})}+{α_{2}}{HG_{2}}exp{(i{φ_{2}})}\ \ \ (7) \)

Where E is the electric field intensity, α₁ and α₂ are intensity coefficients, HG₁ and HG₂ are mode numbers, and φ₁ and φ₂ are phases.

Based on the superposition of two modes, it can be further extended to the coherent superposition of multiple modes, as shown in equation (8):

\( E(x,y,z)={α_{1}}{HG_{1}}exp{(i{φ_{1}})}+{α_{2}}{HG_{2}}exp{(i{φ_{2}})}+⋯+{α_{n}}{HG_{n}}exp{(i{φ_{n}})}\ \ \ (8) \)

represented by the sum formula:

\( E(x,y,z)=\sum _{1}^{K}{α_{K}}{HG_{{m_{K}},{n_{K}}}}exp{(i{φ_{K}})}\ \ \ (9) \)

3. Numerical simulation

Through the above theoretical analysis, this paper simulates the coherent superposition of the first three-orders of HG beams, and obtains the structured beams.

3.1. Coherent superposition of first-order HG beams

The structured beam is obtained by the coherent superposition of the first-order HG beams (HG₀₁+HG₁₀). The intensity coefficient α_K is set to 1:1, and the phase φ_K interval is set to π/4. Through the simulation, 25 patterns are obtained. There are 5 different patterns, as shown in Figure 1.

3.2. Coherent superposition of second-order HG beams

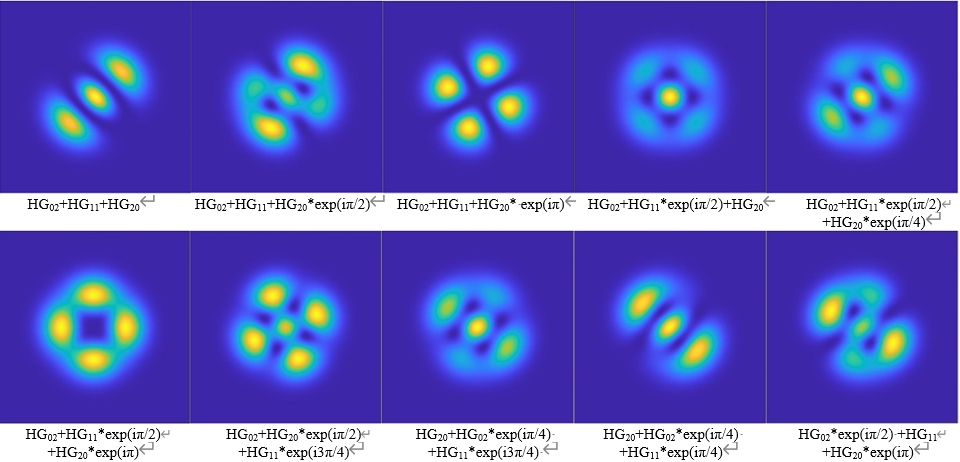
The structured beam is obtained by the coherent superposition of the second-order HG beams (HG₀₂+HG₁₁+HG₂₀). The intensity coefficient α_K is set to 1:1, and the phase φ_K interval is set to π/4. Through the simulation, 125 patterns are obtained. Among them, there are 31 different patterns, and 10 typical structures beams are selected from them and listed in Figure 2.

3.3. Coherent superposition of third-order HG beams

The structured beam is obtained by the coherent superposition of the third-order HG beams (HG₀₃+HG₁₂+HG₂₁+HG₃₀). The intensity coefficient α_K is set to 1:1:1:1:1, and the phase φ_K interval is set to π/4. Through the simulation, 625 patterns are obtained. Among them, there are 189 different patterns from which 10 typical spatial structure beams are selected and listed in Figure 3.

4. Experiments

4.1. Introduction to Experimental System

The experimental system mainly includes: a fiber-coupled 808 nm semiconductor laser, a coupling lens group, a microchip resonator, a polarizing prism, and a CCD camera. The schematic diagram and physical setup of the experimental system are shown in the Figure 4.

4.2. Experimental pattern

Firstly, under the condition of normal incidence of the laser beam, different first-order structure beam outputs are obtained by changing the pump power. Figure 5(a)-(c) shows three different first-order structure beams, and Figure 5(a) shows the spot obtained when the pump power is 3.1 W. Compared with the simulation results, it can be concluded that it is HG01; as the pump power increases to 3.3 W, the facula is consistent with the simulation results of HG₀₁+HG₁₀. With the further increase of the pump power (3.5 W), the light spot changes, corresponding to the simulation results, the available light spot is the coherent superposition after the phase difference between HG₀₁ and HG₁₀ (HG₀₁+HG₁₀*exp(iπ/4)).

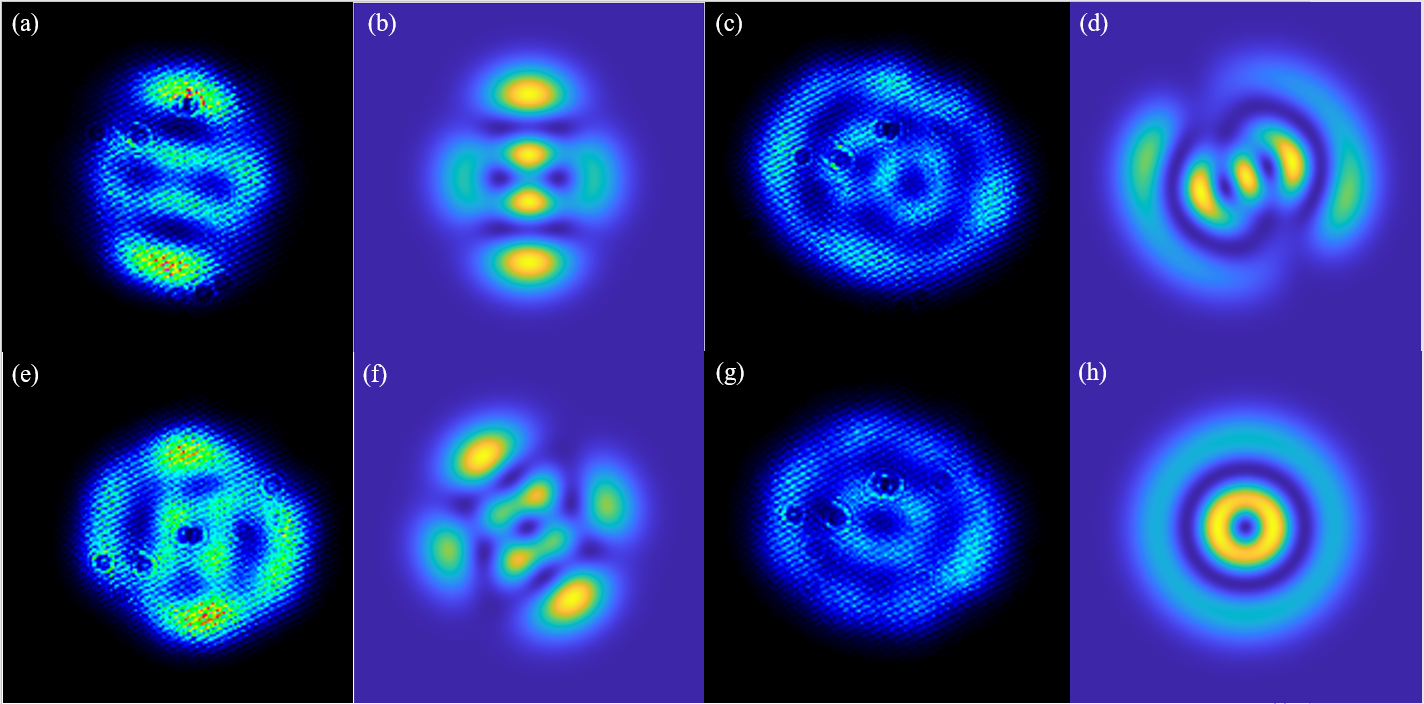
At the same time, under the condition of the same pump power (3.5 W), the structured beam in Figure 6 is obtained by adjusting the angle of the pump light. The appearance of different structured beams is due to the difference in the gain distribution by adjusting the angle of the pumped light, resulting in a change in the mode distribution.

Figure 6(a) and (b) are the experimental and simulation results respectively. HG₂₀ and HG₀₃ were coherently superimposed through the aforementioned eigenmode superposition theory. By comparing the above simulated coherent superposition results with the experimental patterns, the experimental results are consistent with the simulation results. Figures 6(c) and (d), 6(e) and (f), and 6(g) and (h) are the corresponding experimental and simulation results. Table 1. lists the specific intensity coefficients and phase parameters used in the simulation in Figure 6.

5. Conclusion

This paper firstly analyzes the basic theories of structured beams, and uses the eigenmode superposition theory to explain the formation mechanism of structured beams when there are multiple transverse modes and phase differences. Based on the eigenmode superposition theory, the intensity coefficient α_K is set to 1, and the phase φ_K interval is set to π/4, and the simulated structured beams were obtained by the coherent superposition of the first-order, second-order and third-order HG eigenmodes. The first-order structured beams exist 25 combinations, of which there are only 5 different patterns; there are 125 combinations of second-order structured beams, of which there are 31 different patterns; after the superposition of third-order HG eigenmodes, there are 625 combinations, of which 186 different pattens. Finally, by comparing the experimental results with the simulation results, it can be concluded that the experimental results are in good agreement with the theoretical simulation results. It is fully proved that the transverse mode superposition method is an effective way to generate beams with complex spatial structures.