1. Introduction

Quantum mechanics is a revolution in the micro part of classical physics. Quantum mechanics says that the microscopic system can't think of a as being made up of parts that can be separated [1]. It was proposed by many famous physicists in the early 20th century and is important subject of modern physics together with relativity. Quantum mechanics focuses on the fundamental theory of the structure and properties of atoms, molecules, condensed matter, atomic nuclei, and elementary particles.

Quantum state is the basic definition of quantum mechanics. Quantum state represents the state that a quantum system has at a certain time. It is even more important for the basic concept of quantum states and for further operations on top of this basic concept. The study of quantum states is no longer limited to itself. Because of its fundamental properties, the study of quantum states tends to cooperate with other fields of quantum mechanics to build on it. For example, in the application of quantum mechanics, the preparation, coherence and manipulation of quantum states play an extremely important role.

The quantum measurement is also introduced in this paper. Quantum measurement is an important way to define the quantum state. It is difficult for scientists to grasp the real state of a quantum system because of its uncertainty principle and unreproducible properties for unknown quantum states. For example, in the mixed state and superposition state of quantum system, the specific state can’t be easily identified. Only the probability of occurrence of different quantum states can be predicted. The development of quantum computer is introduced in this paper. Quantum computer is one of the core goals of quantum informatics. The research of quantum information science injects new vitality into physics, information science, material science and even the whole science, and at the same time has a profound impact on promoting the development of related high and new technologies and the progress of human society [2]. The rest part of the paper is organized as follows. The second Sec. 2 of the article is about the quantum states. It introduced the basic definition of the quantum state. In addition, different categories of quantum states. It includes pure state mixed state, and superposition state. The 3rd section is about several development upon the quantum states. The quantum measurement and quantum teleportation. Its main point of this paragraph. In the next paragraph, the article focuses on quantum computer which is one of the most important applications of quantum physics. In the 5th Section, the limitation and disadvantage of quantum physics is shown. Eventually, a brief summary is given in Sec. 6.

2. Quantum state

In quantum physics, quantum state refers to any possible state that a quantum mechanical system may exist, which contains all the information of the system [1]. A quantum is a representation of the smallest indivisible fundamental unit of matter. Quantum states are usually expressed in the form of basis vector, wave function, density matrix, etc. The basis vector is in Dirac notation. They are vectors in the Hilbert space. The basis vectors can also be converted to matrix form. In the Copenhagen interpretation, the quantum state is defined by means of operational definition: the quantum state can be identified from a series of preparation procedures, that is, the quantum system produced by this procedure has the quantum state [2]. In the early 20th century, physicists discovered many novel quantum phenomena completely unexplained by classical physics through experiments on small scales of microscopic physics. The Copenhagen interpretation attempts to explain the experimental results and related theories reasonably within the scope of experimental support. Quantum states can be divided into pure states and mixed states. A pure state means that one has definite information about the state of a quantum system. Pure state is any set of base vector coherent superposition state, when |ψ⟩ is said to be random pure state [3]. The equation below is the equation for pure states.

\( |ψ \gt =\sum _{n}{C_{n}}|n \gt \) (1)

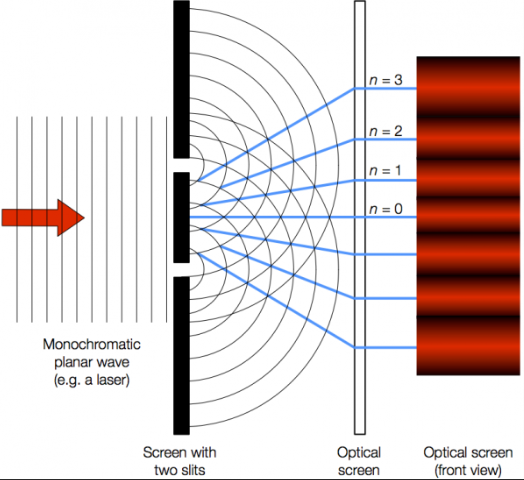
Figure. 1 Diagram of electron double slit diffraction.

If a quantum system is made up of subsystems described by many different state vectors each subsystem appears within the system with a certain probability. This system is called the mixed state is a probabilistic mixture of pure states. For example, studying a quantum system consisting of N atoms, if each atom is in the same state, the system is in a pure state. On the contrary, if the states of N atoms are different from each other, the system is not in a pure state [3], and a state vector cannot be used to describe the state of the system. Statistics for the same quantum mixed states is obtained, should be in quantum mixed states is |ψ1⟩, |ψ2⟩, ... |ψn⟩ in probability P1, P2,..., Pn status [3]. Quantum mixed states are difficult to represent by state vectors in Hilbert space. This is because there is no precise state to describe the state of a quantum system. This is mainly due to the nature of quantum states. Since a mixed state is a combination of a single quantum pure state. Every pure state can appear in a vector in a Hilbert space. Thus, for a quantum mixed state it's going to be multiple state vectors in a Hilbert space. Mixed states are difficult to represent in vector form. Density matrix form is a good representation method.

In quantum mechanics, the principle of superposition states that if the quantum state of a quantum system can be any one of many different quantum states, then their normalized linear combination can also be its quantum state [4]. This linear combination is called a superposition state. The superposition state is different from the mixed state. Even though none of them know the quantum state. Superposition states are also quantum pure states. This is because when one measures a quantum system, the superposition state collapses into a known state, after which the system always remains in an exact state. This state, in the end, can be described by an exact state vector in a Hilbert space.

The superposition of quantum states was discovered through Young's double slit interference experiment. They found that when the emitter emits one electron in a row. The sensor shows that when the number of electrons is large enough. The interference pattern appears. After that, scientists tried to put detectors on the gap to figure out the exact route of the electrons. This action, however, leads to the disappearance of the interference pattern (seen from Fig. 1).

3. Further development on quantum state

3.1. Quantum measurement

In classical mechanics, when the initial conditions and forces on an object are given. The next motion of the object is completely determinable. According to classical mechanics, Laplace, a French mathematician and astronomer, believed that the motion of everything in the universe could be accurately calculated and predicted [5]. Such understanding is no longer applicable when physics comes to the microscopic realms of atoms and quanta. The uncertainty principle was established by studying the motion of electrons in Wilson's cloud chamber. A cloud chamber filled with supersaturated steam, invented by England's Wilson, was a device for twentieth-century beginners to study the behaviour of charged particles. Heisenberg, the discoverer of the uncertainty relationship, questioned the idea that the trails of water droplets in a cloud chamber were electron tracks. Because the fog trails formed by the water droplets in the steam are just too big for the electrons. This means that "what one observed is not the true trajectory of the electron, but rather a rather imprecise sequence of positions marked by small water droplets in the cloud chamber, and the corresponding velocity values between every two such positions are uncertain [6]. On this basis, Heisenberg further deduced: Δp∙Δq≥h/2 (2).

The uncertainty principle mainly puts forward the influence of the unavoidable interference on the experimental results in the measurement quantum process. Heisenberg believed that if the position of an object was to be elucidated, then it was necessary to describe an experiment in which the 'electron position' could be measured, otherwise the elucidations would be meaningless. In the experiment, the interaction between the observation system and the observation object is inevitable. The interference from this interaction is usually negligible for macroscopic objects, but not for microscopic particles.

Quantum measurement refers to the measurement technique that uses the properties of quantum to gain higher skills. To determine the state of the quantum. The uncertainty principle tells us that the measurement of a quantum state causes a change in the quantum state itself. Because the observing system interacts with the observing object. It is therefore important to develop a technique that can measure the state of a quantum by exploiting its properties.

When a single pure quantum state is measured, a situation in which the wave packet collapses occurs. The result will be the intrinsic value of the quantum after collapse, and subsequent measurements of the quantum state will be the same. It is assumed that the mixed state is measured rather than a single quantum system is measured and an exact result is read. For this purpose, the concept of density matrix is applied to describe the state of the measured system.

In order to solve the measurement problem of quantum states, as early as 1852, Stokes proposed a method to approximate the measurement of quantum states through experiments, and proposed a scheme to uniquely determine the polarization state of polarized light through the experimental measurement of four parameters, which was later called quantum chromatography technology [7]. Based on measuring multiple identical copies of the target quantum state, quantum chromatography can obtain the density matrix of the quantum state through linear transformation of the obtained experimental data, so as to obtain all the information of the quantum state [8]. So far, a number of different quantum states have been successfully measured by a number of different groups. In 1993, for example, a team led by Smiths and Beck successfully measured quantum compressed and vacuum states using quantum homodynasty-sounding tomography. Here is an example of how quantum chromatography can determine the density matrix of quantum states using polarized photons. The whole process is mainly divided into four parts, which are to pass n copies of the photon to be measured through four wave plates. They are horizontal polarization (n1), vertical polarization (n2), left-handed direction (n3), and right-handed direction (n4). Thus, the density matrix of the photon to be measured can be constructed from (n0, n1, n2, n3).

3.2. Quantum teleportation

Teleportation, in its early days, was the transmission of an object from the sender to a distant receiver in space. This seems possible as long as humans can gather all the information a substance has. But in fact, because of the uncertainty principle of quantum state, it is very difficult to extract all the information of a quantum, and this teleportation seems impossible to achieve. But in 1993 Charles Bennett and five other scientists discovered that it was possible to transmit unknown quantum states using a combination of EPR channels and classical information, a feat achieved over long distances.

Quantum teleportation is the restoration of an unknown quantum state at ground A to ground B. One can extract all the information of the original quantum state precisely because of the uncertainty principle. Therefore, all the information of the original quantum state must be divided into classical information and quantum information. They are sent to place B by classical channel and quantum channel respectively. Based on this information, the whole picture of the original quantum state is constructed in place B [9].

This pair of quantum states in A and B are actually EPR pairs. The two share an entangled quantum channel. The information of the original object needs to be divided into classical information and quantum information, and then sent to the receiver through their respective channels [10]. Classical information is mainly obtained from some measurement of the original object by the sender. The recipient of the message can use it to create a replica of the original. Specifically, the Bell basis measurement is carried out for the unknown quantum state transmitted to another particle of EPR pair. Due to the non-local correlation property of EPR pair, the quantum information of unknown state will be transferred to another example. Thus, the unknown state can be reproduced on the second particle of EPR pair.

4. The state-of-art applications

The quantum computer is one of the applications of quantum physics. It focusing on using less resources than classical computer and achieve greater calculation ability. This is achieved by implementing quantum computing. Quantum computing is a new computing mode that regulates quantum information units in accordance with the laws of quantum mechanics [11]. The quantum state is the form of memory unit and information storage, and the representation of classical data in the quantum system. When quantum computers were first proposed, scientists were not interest about it. Until Shor's algorithm came along, which included factorization of large numbers and discrete logarithms. It provides exponential acceleration of the best classical algorithms [12]. Since quantum computers have proven to be much more advanced than compact computers, there has been a huge increase in power. Now all countries in the world are gradually focusing on quantum computers. Superconducting quantum computing is one of the points of quantum computers. Superconducting quantum computing uses quantum states of superconducting systems. Therefore, it has harsh requirements on the physical environment. Computers need to work at very low temperatures. This kind of system is widely used in many scientific research institutions and international companies in the world have adopted this kind of system as the research and development basis of their quantum computers. In 2016, IBM launched a 5-qubit superconducting quantum computing platform. In 2017, IBM followed up by announcing the success of a prototype of the 50-qubit quantum computing principle. Then, in 2018, Google successfully developed a 72-qubit superconducting quantum computer [11]. Pan Jianwei's team in China has successfully built a 76-photon quantum computing prototype. This quantum computer can calculate the results of a Gaussian Boson sample in 200 seconds. It would take about 100 million years to figure that out, compared with supercomputers of the same age.

5. Limitations & prospects

Quantum computers are unquestionably more advanced than classical computers. Quantum computers use the properties of qubits to achieve unrivalled computing power. Its computational power exceeds that of a supercomputer by orders of magnitude. But that doesn't mean quantum computers have completely surpassed classical computers. Quantum computers are limited in many ways. To this day, the manipulation and preparation of quantum states is still a sophisticated technology. The practical application of quantum computer is limited by many experimental factors such as quantum bit, quantum gate quality and quantum operating system [13]. Although quantum computers have excellent computing power, their applications are narrow. Classical computer after years of development, now widely used in many industries. As in quantum computing, junior scientists are reluctant to work on this project precisely because, although scientists believe it has the power to transcend classical computing, no meaningful urgent and important application scenarios have been found. And the quantum computers being developed by many companies and countries today are mainly superconducting computers, which need to work at extremely low temperatures. The cost of the entire computer is very high. Well, at the same time, there is a probability that the computer will make mistakes in the process of calculation. In the early days of the development of quantum computers, the probability of error was very high, until the continuous development of technology has reduced the error.

Although the computer has its limitations, quantum computers will play a very important role in the future. Quantum computers can be used to simulate quantum phenomena. They can help model the structure of proteins, develop drugs, or develop new materials. In some chemical and pharmaceutical fields, there is already a large demand for molecular simulation, and this pressure on the classical computer has gradually emerged, and the volume computer can replace the classical computer. Quantum computers also have potential applications in artificial intelligence. The development of artificial intelligence needs a huge amount of computing power to build its logic system for artificial intelligence, while the powerful computing power of quantum computer can just replace the classical computer and give play to the advantages of computing power. Another is cryptanalysis, where quantum computing deciphers many publicly available systems of keys. In order to counter cryptographers, new public key systems and anti - quantum cryptography systems are constructed. Today's cryptographic system has not been proven to be completely secure, so its security is always under threat. The appearance of quantum secure communication also brings a new encryption method, which can improve the security performance. A computer is an essential part of this.

6. Conclusion

In summary, the knowledge of quantum state and quantum measurement and the prospect of the future are introduced. It mainly involves the basic definition of quantum state and some difficulties in quantum mechanics in how to make further measurement of quantum state and the measurement of quantum state. It allows the reader to have a certain understanding of some fundamental parts of quantum mechanics. The pure state, mixed state and superposition state of quantum states are mainly introduced, and the different properties of different states and the expression methods of states in mathematics are also involved. Subsequently, the text focuses on the uncertain properties of quantum states, introduces the difficulties in measuring specific states, and provides one of the current methods for measuring quantum states, quantum chromatography. Finally, some references are provided for the future application of quantum measurement and quantum states, which completes the introduction to the basics of quantum states and measurement. These results offer a guideline for further exploration of quantum techniques.