1. Introduction

In the current world, nanotechnology has become one of the popular areas that plenty of scientists would like to get involved in. The fundamental knowledge of this area would be cell biology, fluid dynamics, mechanical engineering, and math.

In biology, bacteria cells are composed of many different parts. In the most general form, the important parts in a bacterium cell are circular chromosomes, cell membrane, mitochondria, ribosomes, cytosol, cilia, flagella, and potentially the cell wall [1]. The circular chromosomes, DNA double helix strands, are a major part of inherent information storage [2]. The cell membrane and the appendix of it, the extracellular matrix (ECM) is the major part for substance exchanging and selective permeability, and the cell wall is for structural support and gap junctions to transmit signals [3]. The cytosol is the liquid within the cell and the ribosomes are the major components for nutrients and harmful substance breaking down purpose [1]. The mitochondria would serve the purpose of synthesizing ATP from ADP and Phosphate ions which would provide energy source for the cell, especially for cilia and flagella to sense, move and acquire nutrients from the nearby environments [1, 4, 5].

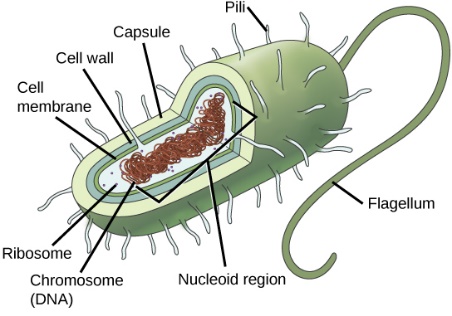
Figure 1. General Biological Bacteria Structure. Drawn by S. Baron. Inc Galveston (TX): University of Texas Medical Branch at Galveston. (http://www.ncbi.nlm.nih.gov/books/NBK7627/).

For the project, it is necessary to state two of the important structures – cell wall and the flagellum [6]. The cell wall supports the bacteria structure, and the flagellum provides the cell with the power of moving forward. During the power providing process, the flagellum structure would swirl, like the function of a motor, by using the energy provided in mitochondria and provide the cell body with a motion.

In the area of engineering, it would be necessary to focus on the living environment of the bacteria and the specific motion production of the bacteria cells. To serve the purpose of nanorobots, the bacteria cells that are researched specifically live in the liquid. Due to the small size of the cells, usually less than 100 micrometers in diameter, the water would be extremely viscous to the organisms or other objects at that size, usually called “low Reynolds number” environment [7, 8]. For the living organisms with naked-eye-visible size, such as mammals and reptiles, water would be a “high Reynolds number” environment [9]. In specific, Reynolds number is defined by multiple factors,

\( Re=\frac{ρUL}{η}\ \ \ (1) \)

where ρ is the density of the fluid, η is the viscosity of the fluid, U is the velocity of the fluid, and L is the length that the fluid passes [9]. If the Reynolds number is smaller than 2300, then it would be dominated by laminar flow which would lead to a rather viscous environment for the swimmer [10]. Also, not only the outside environment would impact the moving speed of the bacteria cell, its own cell size, flagellum size, and flagellum pitch angle would also affect the velocity of itself [11].

The core part of this research is to simulate the bacteria cell response to low Reynolds environment from a macroscopic view. As a result, it is necessary to magnify the size of the cell into a model. In this case, math knowledge is used to impose the dimensional analysis by using the Buckingham Pi Theorem in order to amplify the scale of the cell while maintaining it in a similar low Reynolds environment. The Buckingham Pi Theorem would be able to help calculate the amplification magnitude by using different Π values to induce dimensionless analysis [12] in order to get a possible model scale. It is desired to have a successful test to prove the macroscopic simulation would be a possible way to be a pilot foundation of future nanorobotics and provide a possibility of building nanorobots in the future.

2. Methods

In order to construct the model with the best power efficiency, it is necessary to find the best pitch angle for the model flagellum by using the MATLAB. After getting the pitch, it is ideal to use the dimensions from the MATLAB code to induce an amplification to a real model size. With the best efficiency and the dimensions modified, it would be much easier to construct the model by using the SOLIDWORKS.

In order to create a MATLAB code, the prior thing is to construct some reasonable cell size. Then set the range of the pitch angles from 0 to 90° (0 to 0.5π) by a gradient of 0.01 radians per time, and induce the mechanical equations required to calculate the corresponding swimming time (Appendix A). Record the pitch angle (x-variable) for the maximum speed (y-variable) for later use.

Use the dimensional variables used in the MATLAB part and place them into the dimensional analysis. The first thing to do is to use the Buckingham Pi Theorem to calculate the variable n, m, and r in order to induce a certain number of πs. Then use different πs to calculate the dimensions of the newly constructed math model. If the model’s dimensions do not fit the centimeter scale, amplify the model’s scale by multiplying a certain value to make it reasonable and fit in the centimeter scale (length around 20 to 30 cm).

The most important step to create the model is to build and print the 3D model. This model requires an energy provider, either motor or winder. Use the SOLIDWORKS part to construct two hemispheres and a helix structure with the dimension calculated in the new dimensions. Change the pitch angle of the helix to the one with the maximum velocity. Use an Ultimaker PLA printer to print the sphere parts and the helix part. After all the parts are created and successfully printed, starting the assembly process.

Place the motor set or the winder in one hemisphere and use the epoxy to stick the device on the wall of the hemisphere. During this process, it is necessary to hold the parts together until the epoxy cures. After the epoxy cures, find a correct spot on the other hemisphere to let the flagellum part go through; label that part and then use a drill to make a hole. Use the epoxy to stick the flagellum to the motor or the winder. Hold till it cures, and then stick the two hemispheres together.

The last step is to test the viability of the product prototype and then record the data. Fill a tank with water, and the other one with detergent. Use a marker to label the starting points of the prototype. Use different rounds of motor or winder to check the moving distance of the prototype in the tank with water and detergent respectively. Record the corresponding data. Use MATLAB to process the data in order to get the average moving distance with respect to each solution with different rounds. Use Excel to calculate the best fit curve and plot all the data on a MATLAB graph.

3. Result

The MATLAB code to check the efficiency of different pitch angles would show that at around 0.8 radian (around 45°), the velocity would reach its maximum for a cell (fig. 2).

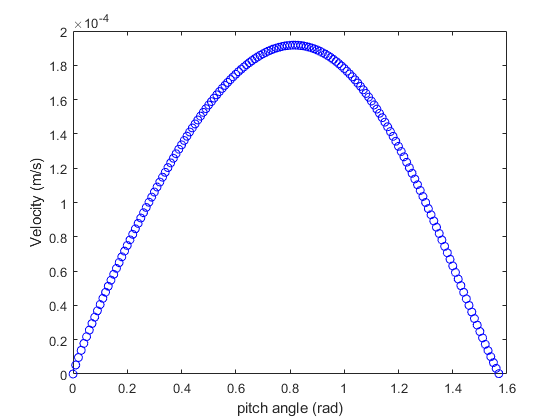
Figure 2. MATLAB figure of the relationship between pitch angle and velocity.

The dimensional analysis would show that the model’s size would be millimeter size. As a result, it is necessary to multiply it by some factor to make it into the centimeter scale.

The SOLIDWORKS modeling and 3D printing would provide a reasonable cell structure (fig. 3) (Appendix B).

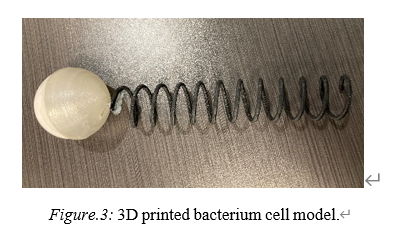
Figure 3. A 3D printed Bacterium Cell Model.

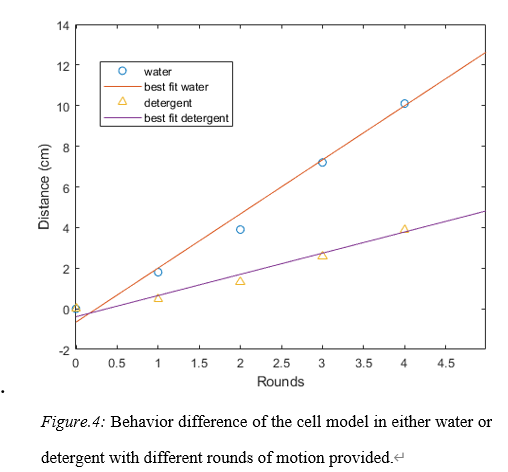
Figure 4. Behavior difference of the cell model in either water or detergent with different rounds of motion provided.

The final testing process would provide the behavior difference of the cell in water and detergent (fig. 4) (Appendix C). In water, the rotation speed would be 2.5 rounds per second in the 5 second test and 2.663 cm forward per second. In detergent, the rotation speed would be 3.57 rounds per second in the 5 second test and the moving speed would be 1.043 cm per second.

4. Discussion

During the 3D printing process, Ultimaker PLA is good for printing the hemispheres, but not good at printing the helix part. It has been tried 6 times on the machine to print the helix part, and only one of them formed a rough shape but extremely fragile. Due to the difficulty of printing helix on the Ultimaker PLA machine, the faculty in the 3D printing lab suggested to use the Stratasys ABS M30 or Formlabs SLS powders using Nylon 12 to form the helix structure. The Formlabs machine would create the structure by adding melted material to the correct spot of the structure while the Stratasys would form a dissolvable support that could be removed after the structure is constructed. The black helix in the final prototype is the Stratasys ABS M30 plastic (fig. 3).

During the earlier testing process, it has been discovered that the ABS helix does not provide a forward motion due to some reason. It was found that the helix was constructed in the opposite direction which would contribute to the backward motion. In order to solve that problem, it is necessary to change the direction of the helix. Due to the time deficiency, it is not possible to re-print another helix by using the Stratasys machine because it takes days to print that helix. In order to solve that problem, the ABS helix is replaced by the metal wire which is hard enough to provide motion without shaking (fig. 5).

Figure 5. New constructed cell simulation with cell body and flagellum.

From the data chart, it could be told that the relationship between the rounds of turning and the distance traveled in both solutions are nearly linear. However, there is a tiny trend of parabola, non-linear, increase of the speed. The reason for that to happen might be the winder inside the cell body. It is known that a regular winder would provide the maximum torque when the memory metal reached its maximum tension. The less memory metal folds, the less torque it would provide. As a result, the original starting torque difference might cause the non-linear shape in the relationship in the diagram.

From the data acquired, it could be told that the traveling distance of the cell simulator is not very apparent. The reason contributing to the tiny difference might come from the lack of energy of the winder that is chosen. Another possible reason for that to happen might be because of the heaviness of the cell body. The cell body is massive and heavy, while the flagellum is thin and weak. In this case, the flagellum would not provide enough forward motion to the cell, so the cell would not travel far to make the result more obvious. In conclusion, this cell simulator would work in a relatively low Reynolds environment, but not very effectively.

5. Conclusion

In conclusion, a simulated macroscale simulation of the constructed cell model would not be compatible to the real-life bacteria micro-swimmers. In theory, micro-swimmers would move in a faster speed in a low Reynolds number condition where in this case, the simulator would move faster in a larger Reynolds number condition. Thus, this simulation experiment would not prove that macroscale simulator would be an appropriate way to simulate small organism in the same condition.