1. Introduction

In recent years, remote sensing technology has rapidly evolved and found widespread use in numerous industries and daily life applications [1]. Today, positioning services are an omnipresent aspect of social production and daily life. They have a vital function in various fields, such as warehouse management, fire rescue, and intelligent factories. It has wide-ranging potential for implementation in wireless communication, radar tracking, and accurate positioning [2]. Compared to other radio equipment, UWB technology offers several advantages including a high system capacity, rapid transmission speed, superior transmission power, robust system confidentiality and pinpoint positioning accuracy [3]. Ultra-wideband (UWB) technology has made significant strides, especially with the rise of the 5G era. Consequently, an increasing number of people seek to use UWB for information exchange between their mobile communication devices. UWB wireless access is an area of emerging research interest and has attracted significant attention, with numerous studies conducted both nationally and internationally. These investigations have encompassed the assessment of UWB system performance, the examination of UWB evolution, the scrutiny of key technologies, and additional topics. Nonetheless, there exist unresolved matters that necessitate deliberation and the possibility of refining. Ultra-wideband technology (UWB) facilitates location using three primary algorithms: time-of-flight (TOF), time-difference-of-arrival (TDOA), and angle-of-arrival (AOA), which leverage UWB's unique, short-pulse signal time-delay characteristics [4]. The accuracy of the indoor positioning system, which utilizes UWB, can be affected by different factors like signal strength, environmental factors, propagation models, and the algorithms used for positioning. In this paper, we examine the signal characteristics and positioning accuracy of ultra-wideband (UWB) technology. This paper also discusses how to enhance the indoor positioning method and positioning algorithm using trilateral measurement and the time-of-arrival (TOA) positioning method to improve UWB's wireless communication technology's positioning effect.

2. Introduction of indoor positioning technology

While outdoor positioning relies heavily on global positioning system (GPS) signals, achieving indoor positioning is much more challenging as GPS signals have weak penetration, rendering them unsuitable for indoor tracking. Several indoor positioning techniques, including Easy Living, Wi-Fi, Data Rate, and UWB, have been proposed [5]. However, the positioning system used by Easy Living utilises computer vision technology for recognition [6]. Although the Easy Living calculation has the capability to identify multiple target states simultaneously, the process is intricate and necessitates costly equipment expenses. Ultra-wideband (UWB) is a promising solution for indoor positioning due to its low energy consumption, high penetration, and strong anti-interference properties and has, therefore, received significant attention. The indoor positioning system mainly utilizes wireless communication integration, base station positioning, inertial positioning, and other technologies to establish an indoor ranging and positioning system [7]. They are capable of identifying individuals and objects for indoor location monitoring. Other common indoor positioning technologies include Wi-Fi, Bluetooth, infrared, ultrasound, and UWB. Unlike other wireless technologies, UWB operates through radio pulses. It employs a sequence of pulses over a wide range of frequencies and is widely recognised as pulse radio UWB.

3. UWB wireless positioning principle and improving method

3.1. Trilateral measurement

3.1.1. Principle. The trilateral measuring technique ascertains the positioning of a node by measuring the distance between three or more reference nodes and the target node. This is done to calculate the coordinates of the target node [8, 9]. The principle is illustrated in Figure 1 depicted below:

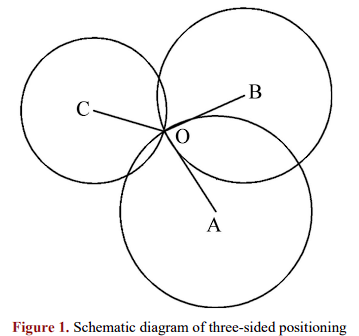
Figure 1. Schematic Diagram of Three-Side Positioning [10].

As depicted in the above figure, the reference nodes consist of A, B, and C, with their corresponding coordinates ( \( {x_{a}} \) , \( {y_{a}} \) ), ( \( {x_{b}} \) , \( {y_{b}} \) ), and ( \( {x_{c}} \) , \( {y_{c}} \) ). The distances between the three nodes and the undetermined node O are \( {d_{a}} \) , \( {d_{b}} \) , and \( {d_{c}} \) respectively. Similarly, the distances between the node to be determined and the three reference nodes are also \( {d_{a}} \) , \( {d_{b}} \) , and \( {d_{c}} \) , respectively. Additionally, the distances from the node in question to the reference nodes serve as the radius of a circle with each reference node as its centre. The coordinates of the node to be determined are obtained from the intersection of the three circles [10]. Solving:

\( \begin{cases} \begin{array}{c} \sqrt[]{{(x-{x_{a}})^{2}}+{(y-{y_{a}})^{2}}}={ⅆ_{a}} \\ \sqrt[]{{(x-{x_{b}})^{2}}+{(y-{y_{b}})^{2}}}={ⅆ_{b}} \\ \sqrt[]{{(x-{x_{C}})^{2}}+{(y-{y_{C}})^{2}}}={ⅆ_{C}} \end{array} \end{cases}\ \ \ (1) \)

Get the coordinates of node 0:

\( [\begin{matrix}x \\ y \\ \end{matrix}]={[\begin{matrix}2({x_{a}}-{x_{c}}) 2({y_{a}}-{y_{C}}) \\ 2({x_{b}}-{x_{c}}) 2({y_{b}}-{y_{c}}) \\ \end{matrix}]^{-1}}[\begin{matrix}x_{a}^{2}-x_{c}^{2}+y_{a}^{2}-y_{c}^{2}+d_{c}^{2}-d_{a}^{2} \\ x_{b}^{2}-x_{c}^{2}+y_{b}^{2}-y_{c}^{2}+d_{c}^{2}-d_{b}^{2} \\ \end{matrix}]\ \ \ (2) \)

3.1.2. Error analysis. Let the error ranges of nodes d and a, b, and c be respectively \( {\widetilde{d}_{a}} \) , \( {\widetilde{d}_{b}} \) , \( {\widetilde{d}_{c}} \) . The distance error \( γ \) is defined as the percentage of the distance between the nodes to be compared. \( γ \) is a random number within a certain range. The relationship between range results and range errors is shown in equation (3):

\( \begin{matrix}\widetilde{{d_{i}}}={ⅆ_{i}}+{ε_{i}} \\ {ε_{i}}={γ_{{i^{*}}}}{d_{i}} \\ \end{matrix}, i=a,b,c\ \ \ (3) \)

The actual estimated node coordinates with ranging errors is equation (4):

\( [\begin{matrix}\widetilde{x} \\ \widetilde{y} \\ \end{matrix}]={A^{-1}}\widetilde{E}={A^{-1}}[\begin{matrix}x_{a}^{2}-x_{c}^{2}+y_{a}^{2}-y_{c}^{2}+\widetilde{d}_{c}^{2}-\widetilde{d}_{a}^{2} \\ x_{b}^{2}-x_{c}^{2}+y_{b}^{2}-y_{c}^{2}+\widetilde{d}_{c}^{2}-\widetilde{d}_{b}^{2} \\ \end{matrix}]\ \ \ (4) \)

Equation (4) is subtracted from equation (2) to obtain the node coordinate error equation (5):

\( [\begin{matrix}Δx \\ Δy \\ \end{matrix}]=[\begin{matrix}\widetilde{x} \\ \widetilde{y} \\ \end{matrix}]-[\begin{matrix}x \\ y \\ \end{matrix}] \)

\( ={A^{-1}}[\begin{matrix}(\widetilde{d}_{c}^{2}-d_{c}^{2})+(d_{a}^{2}-\widetilde{d}_{a}^{2}) \\ (\widetilde{d}_{c}^{2}-d_{c}^{2})+(d_{b}^{2}-\widetilde{d}_{b}^{2}) \\ \end{matrix}] \)

\( ={A^{-1}}ΔE={[\begin{matrix}a1 & a2 \\ a3 & a4 \\ \end{matrix}]^{-1}}[\begin{matrix}e1 \\ e2 \\ \end{matrix}] \)

\( \begin{matrix}a1=2({x_{a}}-{x_{c}}) ; a2=2({y_{a}}-{y_{C}}) \\ a3=2({x_{b}}-{x_{c}}) ;a4=2({y_{b}}-{y_{c}}) \\ \end{matrix}\ \ \ (5) \)

Further:

\( {A^{-1}}[\begin{matrix}a1 & a2 \\ a3 & a4 \\ \end{matrix}]=\frac{1}{a1\cdot a4-a2\cdot a3}[\begin{matrix}a4 & -a2 \\ -a3 & a1 \\ \end{matrix}] \)

\( ΔE=[\begin{matrix}e1 \\ e2 \\ \end{matrix}][\begin{matrix}(\widetilde{d}_{c}^{2}-d_{c}^{2})+(d_{a}^{2}-\widetilde{d}_{a}^{2}) \\ (\widetilde{d}_{c}^{2}-d_{c}^{2})+(d_{b}^{2}-\widetilde{d}_{b}^{2}) \\ \end{matrix}] \)

\( =[\begin{matrix}(1-{(\frac{1}{1+{γ_{c}}})^{2}})\cdot \widetilde{d}_{c}^{2}-(1-{(\frac{1}{1+{γ_{a}}})^{2}})\cdot \widetilde{d}_{a}^{2} \\ (1-{(\frac{1}{1+{γ_{c}}})^{2}})\cdot \widetilde{d}_{c}^{2}-(1-{(\frac{1}{1+{γ_{b}}})^{2}})\cdot \widetilde{d}_{b}^{2} \\ \end{matrix}] \ \ \ (6) \)

Eq. 5 is derived by subtracting Eq. 3 from Eq. 4. It is assumed that Eq. 5 may contain a ranging error, and 4-2 is used to quantify the relationship between the ranging error and the final positioning error. Utilizing a transformation in (5) and (6), the linear system of equations is made more concise and substituted into Eq. (3). Thus, the terms and relative magnitudes that affect the final positioning error are derived, which in turn guide the scheduling of anchor nodes.

3.1.3. Improving method. Neighbouring nodes to be located must have at least three anchor nodes present for anchor node selection to take place. Assuming that 10% of the nodes in the network are anchor nodes, the average network connectivity must be greater than 30 before the average number of anchor nodes at a node can be greater than 3. In general, network connectivity greater than 30 is unreasonable, and too much connectivity tends to lead to network congestion. Another method is to increase the ratio of anchor nodes, but increasing the ratio of anchor nodes also brings cost, configuration, and applicability problems. Upgrading non-anchor nodes to anchor nodes would be a more feasible solution. In wireless sensor networks deployed randomly, some nodes possess at least three anchor nodes, whereas others have fewer than three. It is feasible to conduct a triangulated measurement of the positioning of anchor nodes that can be accurately positioned and subsequently elevate their status as anchor nodes. Each positioning cycle increases the quantity of "anchor nodes" and reduces the number of unidentified positioning nodes. Increasing the quantity of "anchor nodes" significantly enhances the localization success rate and boosts the probability of activating the anchor node selection algorithm [11].

3.2. TOA positioning method

3.2.1. Principle. The TOA time-of-flight algorithm is a distance estimation method based on the time delay from the reference node to the target node to obtain the distance between the target node and the reference node. By estimating the distance between three or more reference nodes and the node to be located, the coordinates of the node to be located can be calculated by the three-sided measurement method described above. The TOA ranging algorithm can be divided into One Way Ranging (OWR) and Two Way Ranging (TWR) [12].

3.2.2. One-way ranging. One-way ranging refers to the use of calculating the time of flight of a single signal to estimate the distance when the reference node has the same clock as the node to be located [13]. Nodes communicate between AB, when T₀ moment node A will contain the time identifier of the information packet sent to node B, node B's reception time is T₁, then according to the electromagnetic wave propagation speed in the air is \( 1c=3×{10^{8 }} \) m/s, the distance between the two nodes AB is:

\( S=c({T_{1}}-{T_{2}})\ \ \ (7) \)

3.2.3. Two-way ranging. Two-way ranging is an algorithm that uses the clock of a single node in situations where one-way ranging is not feasible, meaning that the clocks of the reference node and the node to be determined are not synchronized. The algorithm derives the distance between the two nodes by calculating the round-trip time difference of the signal [14, 15]. At T₀, node A sends a data packet to node B. Upon receiving it, node B quickly forwards it back to node A. At T₁, when node A receives the forwarded packet, the distance between nodes AB can be calculated [12].

\( S=\frac{1}{2}c({T_{1}}-{T_{0}})\ \ \ (8) \)

3.2.4. Error analysis. The TOA localization algorithm utilizes the TOA circumferential equation, which is formed from intersecting lines between circles. The equation is composed of various combinations to determine the location. Analyzed from the geometric model, if the signal from the mobile station (s) to the base station (i) propagates in the line-of-sight case (LOS), and the measured distance is taken, the mobile station must be on the circumference of the circle with the base station (i) as the centre and superior as the radius. The measurement equation of Time of Arrival (TOA) when there are three base station coordinates is:

\( {D_{i}}=\sqrt[]{{({x_{i}}-{x_{z}})^{2}}+{({y_{i}}-{y_{z}})^{2}}}\ \ \ (9) \)

Where, ( \( {x_{i}} \) , \( {y_{i}} \) ) is the coordinate of the \( i \) th base station, and ( \( {x_{z}} \) , \( {y_{z}} \) ) is the coordinate of the mobile station \( s \) . The geometry is shown in Figure 2.

Figure 2. 3 TOA geometric model of base station [16].

Two important points to note are:

1) In the 2D planar positioning system, the LLOP method necessitates a minimum of three base stations. Secondly, when the number of base stations exceeds three, the system of equations can be solved using the least squares method.

2) Analyzing the equation, it is necessary for the LLOP method that the base station deployment be in either horizontal or vertical mode. Technical abbreviations should be avoided unless explained first. If the base station is in these modes, achieving positioning will require the redefinition of the base station coordinates and the rotation of the axes before they are turned back to their original positions after the positioning is completed.

In the urban environment, signal propagation between the mobile station and base station is often impeded by buildings. As a result, the signal can only propagate in a non-line-of-sight (NLOS) manner through reflection and refraction. The distance between the signal path and the base station is inevitably longer than in the case of line-of-sight. Using the LLOP method to measure this will result in inaccurate data. The effect of NLOS propagation on wireless positioning must be considered [16].

3.2.5. Improving method. In the NLOS channel, the measured distance from the mobile station to the base station is greater than or equal to the real distance from the mobile station to the base station:

\( {ⅆ_{i}}≥{D_{i}}\ \ \ (10) \)

Where \( {d_{i}} \) is the distance measured in the NLOS channel and \( {D_{i}} \) is the distance measured in the LOS channel. Since \( {d_{i}} \) is always greater than or equal to the true value of the mobile station to the base station, it can be assumed that the distance to the base station after calculating the coordinates of the point of intersection of two circles is always greater than or equal to the distance from the mobile station's true coordinates to the base station under NLOS channel transmission. Based on this consideration, a base station selection and coordinate optimization mechanism is proposed: 1) An initial value coordinate is obtained by measuring the LLOP method; 2) Select at least three base stations so that the initial value coordinates obtained by the LLOP method do not pass the extension lines of the two base stations; 3) Select the base station that meets condition 2, and retain the coordinate value that the measured distance from the mobile station to the base station is less than the distance from the initial coordinate to the base station; 4) When the data obtained by the secondary measurement is not less than the initial value coordinate, the coordinate of the mobile station is the initial value coordinate. Based on the measured values obtained from the above four points, it is possible to continually approximate the coordinate position of the actual moving table to attain accurate positioning [16].

4. Discussion

The precision of UWB can be improved by optimising the algorithms used in Time of Flight (TOF) and Time Difference of Arrival (TDOA). Alternatively, various positioning methods can be combined so that they complement each other, for instance, AOA-TOF, AOA-TDOA, and more. Anchor-based positioning algorithms should optimise the stability and accuracy of the positioning system in the following two aspects: 1. continue to study and optimise the positioning algorithm, reduce the computational complexity time as well as spatial complexity of the positioning algorithm, and continue to improve the positioning accuracy, especially to reduce the error in three-dimensional positioning; 2. promote the development of the hardware that the positioning algorithm depends on, such as improving the measurement accuracy of the anchor point for wireless communication, increasing the communication radius of the wireless communication anchor point, and improving the anti-interference ability of the communication equipment. In the future, it may be beneficial to explore the use of intelligent algorithms paired with wireless positioning technology to enhance algorithmic precision. By combining UWB and GPS and integrating these technologies, there is potential for significantly higher positioning accuracy.

5. Conclusion

The rapid development of communication technology has led to the emergence of numerous new wireless communication services. However, the rigid management of spectrum resources hampers their availability. This has led to a significant scarcity of spectrum resources, which is exacerbated as new services require higher transmission rates from communication systems. Therefore, it is desirable to acquire a transmission approach with decreased costs, elevated transmission velocity, and diminished energy consumption. Ultra-wideband (UWB) is a communication system that utilises narrow pulses for signal transmission, which corresponds better with the above-mentioned criteria. The trilateral measurement and positioning algorithm could suffer substantial errors where the anchor point position approximates a straight line. This paper provides a theoretical analysis of the error associated with the trilateral measurement positioning algorithm, identifies the impact of the anchor point position on positioning accuracy, and proposes algorithms to improve its performance. Additionally, the TOA positioning algorithm provides high accuracy. The accuracy of the algorithm can be improved by selecting the optimal base station and optimizing the intersection point. The current research is more based on existing literature and research results, and future research will explore methods for improving accuracy in conjunction with specific algorithm improvements.

Acknowledgment

I would like to acknowledge those who provided assistance in the completion of this thesis. Firstly, I extend my appreciation to my supervisor for his guidance and unwavering support during the research process. His expertise had a substantial impact on my work, enabling me to overcome challenges and make progress. His advice has piqued my interest in pursuing a research career. Secondly, I would like to express my gratitude to my family and friends for their continuous support and encouragement, which helped me persist and finish this thesis. Their understanding and support were crucial to my progress. Finally, I would like to acknowledge those who assisted my research, whether by providing data, participating in discussions, or offering literature, as their contributions were essential. Without their help, this thesis would not have been possible. Thank you for your assistance. I have gained valuable experience and knowledge during the completion of this dissertation, which I am certain will have a positive impact on my future academic and professional development. Once again, I express my thanks to all who have helped me; your support is priceless.