1. Introduction
Set theory is often attributed as the foundation of modern mathematics. In particular, it is because it was discovered that a fairly large number of mathematical constructs could be expressed inside the set theory [1]. Therefore obviously, the axioms used to regulate the set theory have a great influence on the other mathematical constructs that depend on the set theory. Remarkably, the axiom of choice (AC) is one of the nine axioms in set theory that has played a central role in the development of mathematics. It allows for the construction of subsets by using the choice function to select one element from each set in a collection of sets, even when there are an infinite number of sets or lacking a specific rule for selection. While it was initially controversial when it was introduced by mathematician Ernst Zermelo in 1904, AC has since become widely accepted as a foundational principle in mathematics [2]. However, some counterintuitive applications of the axiom of choice, such as the Banach-Tarski theorem, caused more mathematicians to do research on the axiom of choice, and try to give proofs without using AC. Justification for doing so, according to Ivan Khatchatourian, is that: “Proofs that make no use of AC are usually very constructive, in the sense that if they prove some object exists, they tend to explicitly construct it. Proofs that do use AC often involve steps where we just ask AC to give us elements of sets, and then we work with them even though we know nothing else about them” [3]. It was also discovered that the axiom of choice could be shipped with various strengths, ranging from weak to strong versions [4]. The strength of AC refers to the extent to which people can utilize the axiom of choice [5]. Stronger variants of AC imply AC and often other results, while weaker variants of AC might only allow AC with certain restrictions (like the axiom of countable choice ( A{C_{ω}} ) which only allows selection of elements inside a countable collection of sets). These different variants of AC have significant implications for the foundations and branches of mathematics, and exploring their influence is crucial to understanding the overall structure and development of mathematics. Current research into AC is mainly about resembling a reverse mathematics-like approach to proof theorems or providing mathematical constructions inside certain subbranches without utilizing the axiom of choice or at least only making use of a weak version of it. Hrbacek and G. Katz formulated two axiomatic systems, SPOT (conservative extension of ZF) and SCOT (conservative extension of ZF+DC) for handling infinitesimals in mathematics analysis [6]. Fuchino recently examined, in particular, how AC was applied in the variations of Tychonoff’s Theorem. Harrison-Trainor and Kulshreshtha axiomatized principles needed for reasoning about the size of sets without using AC [7]. These are all specific research in isolated fields about variants of AC. It’s not hard to see that there is a research gap in the high-level examination of the implications of variants of AC. Therefore, the significance of this study lies in its systematic, high-level scrutiny of how various formulations of the Axiom of Choice (AC)—in both its strong and weak variants—affect the very foundations of mathematical theory. By delving into the nuances of different incarnations of this pivotal axiom, the research aims to shed new light on its integral role across multiple mathematical domains. Moreover, the study explores how the relative strength of the Axiom of Choice has consequential ripple effects across various subfields of mathematics. This is not merely an academic exercise; the understanding gleaned has practical applications in elucidating the structural integrity of mathematical objects and the stability of the mathematical constructs they inform. In key areas such as measure theory and mathematical analysis, the veracity of the Axiom of Choice is intimately tied to both foundational postulates and critical theorems. Therefore, a systematic review of the strong and weak variants of AC promises to offer a more organized, comprehensive, and elevated perspective than previous research, which often focused on the axiom’s impact in isolated contexts. In summary, this investigation aims to provide a panoramic view of the Axiom of Choice’s significance, thereby enriching our understanding of its multifaceted impact on the landscape of mathematics.
2. Comparative Analysis
2.1. Preliminaries
Zermelo first formulated the axiom of choice in 1904 in order to establish a fundamental idea of Cantor’s set theory that every set can be well-ordered (known as the well-ordering theorem). However, his introduction of this axiom in 1904, along with its subsequent applications, stirred significant controversy among mathematicians of that era.
2.1.1. Choice function. Suppose there is a non-empty set X , then a choice function for X is a function f:X⟶ ∪X such that f(x)∈X for all x∈X .
2.1.2. Axiom of choice (AC). Any non-empty set X containing non-empty subsets has a choice function.
Unrigorously speaking, AC asserts that there is always a way of choosing elements one by one from a collection of sets, even when the collection is infinite. By using the axiom of choice, Banach and Tarski were able to formulate the Banach-Tarski theorem that allows a ball in a normal Euclidean space to be doubled or even be cloned an infinite number of times [8]. This controversial result is still, to these days, considered to be one of the most unintuitive applications of AC [9].
2.1.3. Negation of the Axiom of choice ( ¬AC ). The following statements are equivalent to ¬AC :
• Failure of the Law of Trichotomy for cardinal (i.e., there could be two incomparable cardinals) [10].
• All subsets of the set of real numbers are measurable.
• Existence of vector spaces which have no basis [11].
2.2. Exploring the Implications of Weak Variants of the Axiom of Choice
2.2.1. Overview of Weak Variants. The Case of AC. There are various weak variants for AC. The first one would be the axiom of dependent choice (DC), which was introduced in 1942 by Paul Bernays during the investigation of new axioms needed for ZFC to develop analysis [12].
(Axiom of Dependent Choice (DC)). Suppose {~_{X}} is a total relation defined on X (i.e. a {~_{X}} b ∨b {~_{X}} a for any a,b in X), then DC could be formalized as the following [13]:
For every non-empty set X , there exists a sequence of objects, {x_{n}} (with n∈N ) such that \lbrace {x_{n}},{x_{n+1}}\rbrace ∈{~_{X}} [14].
The designation “dependent choice” was given because every available choice (made in {x_{n+1}} ) is contingent upon the preceding choice (in {x_{n}} ). Among all the weak variants that were introduced in the paper except BPI, DC was the strongest one.
(Countable Axiom of Choice ( A{C_{ω}} )). For any non-empty countable set X containing non-empty sets, there is a choice function for X .
A{C_{ω}} is strictly weaker than DC [15].
(Axiom of Multiple Choice (MC)). For any non-empty set X containing non-empty sets, there is a function f such that f(x) gives a non-empty finite subset of x for all x∈X .
(Countable Axiom of Multiple Choice (CMC)). For any non-empty countable set X containing non-empty sets, there is a function f such that f(x) gives a non-empty finite subset of x for all x∈X .
MC is equivalent to AC while CMC is implied from CC.
(Finite Axiom of Choice (FAC)). For any non-empty set X containing non-empty finite sets, there is a choice function for X .
(Boolean Prime Ideal (BPI)). A prime ideal exists in every Boolean algebra [16]. BPI implies FAC and the ultrafilter lemma.
(Ultrafilter lemma (UL)). Every filter defined on X could be extended to an ultrafilter.
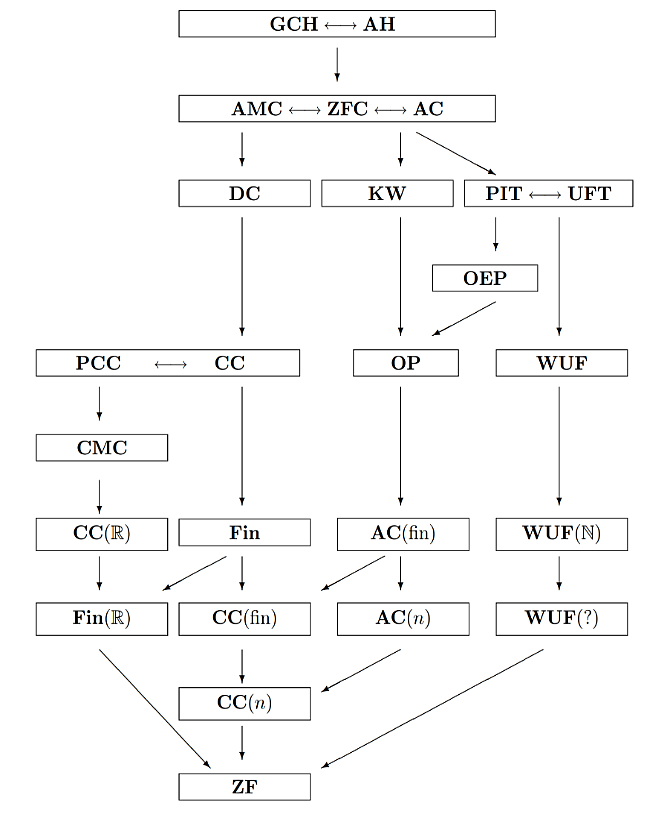
| Figure 1. Axioms strength (decreasing gradually from the top; graph taken from Herrlich, 2006, p. 18). CC is A{C_{ω}} , AC (fin) is FAC, PIT is BPI, UFT is UL, AMC is MC (Photo/Picture credit: Original). |
The Case of ¬AC .
As shown in Figure 1. There are a couple of weak axiom variants that negate AC as well.
2.2.2. Analytical Assessment. In topology, weaker variants of the axiom of choice are already enough for some constructs and theorems in mathematics. Specifically, Keremedis showed that A{C_{ω}} and CMC imply the following four statements [17]:
Metrizable spaces remain metrizable when subjected to countable products (by CMC ).
Second countable spaces remain second countable when taking countable products of them (by A{C_{ω}} ).
First countable spaces preserve their first countability under countable products (by CMC).
Separable Hausdorff space stays separable under countable products (by {AC_{ω}} ).
Howard and Rubin, in their book, also mentioned a couple of other results from A{C_{ω}} in topology:
A Lindelöf property holds for the disjoint union of a countable set of compact {T_{2}} spaces.
Every σ -compact space is Lindelof.
In addition, Kelley’s theorem (or the ultranet’s lemma: every net has a universal subnet) only needs BPI to be proved. In Howard and Rubin’s book, there are a lot of general topological theorems that could be derived from only using A{C_{ω}} , CMC or other weak variants. Even though the full Baire Category theorem, being attributed as “one of the principal avenues through which applications of completeness are made in classical and functional analysis” could not be proved, a special form of Baire Category theorem that only works filter complete metric spaces is provable from DC. According to Jia, the Axiom of Dependent Choice can establish several desirable properties within the field of topology but not beyond that [18].
In fact, the principle of the construction of the ultrafilter (ultrafilter lemma) is directly implied by BPI, which is one of the weak variants of AC. Ultrafilter is one of the important constructions in mathematics that has a lot of profound impacts on not only the subbranches of mathematics but also other scientific studies [19]. Interestingly, one can use ultrafilter to prove Arrow’s theorem in the social choice theory field [20]. Ultrafilter lemma and Tychonoff’s theorem (when applied to Hausdorff spaces) are equivalent as well.
One of the weak variants of the axiom of choice, the ultrafilter lemma or BPI is sufficient to prove the compactness theorem that is fundamental in the field of mathematical logic. The compactness theorem is equivalent to the completeness theorem and could derive a lot of important results in model theory and logic (and also in other fields like combinatorics and algebra), for example, the statement “Every set could be totally ordered”. It could also help to precisely discover and determine the strength of the specific logic systems.
In set theory and model theory, several fundamental theorems could be shown using UL. The presence of ultraproducts that are non-trivial, is one such result [21].
The existence of non-measurable sets is implied by BPI. This phenomenon could be considered to bring new insights into the mathematical landscape and also introduce counterintuitive results like the Banach-Tarski theorem.
In algebra, there are several basic results that could be proved using a weakened variant of the axiom of choice. An example of this is the statement “Every field has an algebraic closure” which is shown to be equivalent to the compactness theorem (and could be deduced from UL or BPI as mentioned before) [22]. Also, using BPI, one can show Stone’s representation theorem for Boolean algebras (which is important as it bridges Boolean algebra with zero-dimensional compact {T_{2}} spaces).
BPI implies the Hahn-Banach theorem, which is an important theorem in the field of functional analysis. The Hahn-Banach theorem shows that on every normed vector space, there exists certain linear functionals. There are also recent works being done by Hrbacek and G. Katz utilizing only DC to create a theory (SCOT, which is a conservative extension based of ZFC+DC) that could used to handle infinitesimals used in non-standard analysis.
2.3. Assessing the Implications of Strong Variants of the Axiom of Choice
2.3.1. Overview of Strong Variants. The case for AC.
There are several strong variants for AC.
Axiom of constructability (V = L). The axiom of constructability could be stated in two forms:
Every set is constructible.
For every set X , there exists an ordinal α , such that X∈{L_{α}} where L is the constructible universe.
Generalized continuum hypothesis (GCH). There exist no intermediate cardinalities between the cardinality of an infinite set and the cardinality of its power set (i.e. {ℵ_{α+1}}={2^{{ℵ_{α}}}} for all ordinal α ) [23].
The case for ¬AC .
There are several strong variants for ¬AC .
Axiom of determinacy (AD). Every set of reals is determined. As shown in Figure 2.
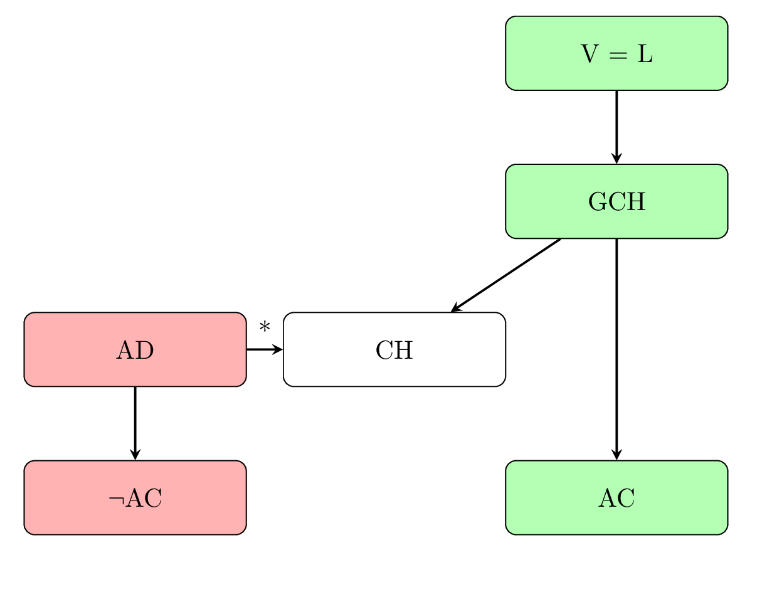
Figure 2. Axioms strength (decreasing gradually from the top). AD only implies a special form of CH that states: There’s no set whose cardinality is strictly between the cardinality of N and the cardinality of R (Corn & Ross, n.d.) (Photo/Picture credit: Original).
2.3.2. Analytical Assessment. The axiom of constructability implies the axiom of choice and notably gives answers to some interesting questions, specifically, V=L implies GCH, the negation of Suslin’s hypothesis and the affirmation of Whitehead’s conjecture [24-26]. Since V=L makes the whole set universe constructible, there exists a well-ordering for V, the class of all sets. However, the problem with V=L is that it greatly limits the ontologies in mathematics, and on some level, strangled the existence of large cardinals [27, 28]. In particular, Scott proved that the existence of measurable cardinal implies V≠L [29]. The research on large cardinals allows (and in fact, is an extremely useful tool for the following): (1) pinpointing the strength of axioms and examining their relationship with large cardinals (one example that was given by Woodin is that extremely large cardinals are at some level, trying to “mimic” the axiom of choice) and (2) use axioms like “The existence of … cardinal” (often referred as large cardinal axioms) to replace common axioms for proving or constructing things (like the Grothendick’s universe) [30]. The adoption of the axiom of constructability would mean giving up on such nice tools, though there has been attempt to bolster this axiom so that the model could hold large cardinals (like Woodin’s Ultimate-L program) [31]. It is also worth known that some mathematicians think that the fact that V=L provides definite answers to certain questions also, on some level, damaged the freedom of the set universe, and they often believed in the multiverse approach [32, 33]. An example of this is that V=L implies GCH, as some would have thought, this ruled out the possibility of theorems and constructs that could be derived from ¬ GCH. Even for a weaker version of GCH, the actual CH, when given a definite answer to (by adopting certain axioms), would have great implications. In fact, Sierpinski demonstrated 82 propositions that were implied from CH [34]. A more general CH allows for a deeper understanding of cardinal arithmetic, set theory and model theory.
Though it has been shown that AD is incompatible with AC, weaker variants such as A{C_{ω}} could still be deduced from AD. Specifically, AD also implies DC in L(R) . A few direct results from AD is that every set of the reals will be Lebesgue measurable, Baire and either has a perfect subset or being a countable set itself [35]. An even stronger version of AD, the A{D^{+}} implies every set of reals being Ramsey, however in 2012 it has been shown by Shao that AD is already sufficient for proving this [36]. Furthermore, AD is incompatible with V=L. AD implies the non-existence of free ultrafilters on ω and the Hamel basis on R over Q as well [37]. There are also some counterintuitive results from the negation of AC (implied by AD). Example of this includes the existence of vector spaces that does not have a basis and the violation of the law of trichotomy for cardinal comparison (i.e., there exists two sets whose cardinals are incomparable).
2.3.3. Recommendations and Broader Implications. There are currently 3 trends in mathematics about the axiom of choice [38]. The first one is to use it without hesitation. The second one is to use AC only when the proof needs it. The last one is to reject AC completely. Mathematicians who have different philosophies choose their approaches differently. In particular, most mathematicians believe in the first approach. There are also few advocators (like Quine) for the adoptions of stronger axioms like V=L or GCH to obtain more useful and interesting results [39]. However, adopting strong axioms also greatly limits the mathematical freedom inside the theory as they restrict certain mathematical constructs inside them (as mentioned in 2.3.2). Researchers who believe in Occam’s razor often choose to go with the second way. Specifically, the reverse mathematics program is one such example that seeks to determine the minimal axioms necessary to prove specific mathematical theorems [40]. Nevertheless, the problem with adopting weak variants of AC is that, while it might prevent certain unintuitive results or possible inconsistencies, certain important, useful and convenient theorems and results (like Tychonoff’s theorem, Zorn’s lemma, the statement “every vector space has a basis”) could not be derived. Meanwhile, the constructivists, criticizing AC for its non-constructiveness, often decide to reject AC completely. Theories like non-standard analysis, which makes extensive use of the axiom of choice, have once received harsh criticism from constructivists (like Bishop) for this reason [41]. However, Herrlich pointed out that, without the axiom of choice, certain important subbranches in mathematics, ranging from cardinal arithmetic in set theory to algebra and topology, would have serious unfixable problems. In fact, even in elementary analysis, there would have unpleasant results without AC, for example, R may fail to be Lindelöf or sequential (i.e. there could exists certain subsets of R that are not closed but are sequentially closed). There are also attempts to adopt the axiom of determinacy or other negation of the axiom of choice. Though it gives nice results (like the fact that ZF+AD implies all subsets of R being Lebesgue measurable), since it contradicts AC, numerous important theorems, as pointed out before, would be impossible to be derived. Finally, there is an approach of adopting a completely different new mathematical framework, like HoTT. However, the problem with this is that it would be very possible to take a long time to migrate existing theorems and theories to the new framework.
3. Conclusion
Overall, this systematic review has revealed that the varying strength of the Axiom of Choice (AC) exerts significant influence on the subbranches and foundational aspects of mathematics. When considering weaker variants of AC, this study examined the potency of these variants and the consequences they hold. Notably, it was determined that a weak form of AC can be sufficient for deriving numerous basic and fundamental theorems in various mathematical subfields, such as topology, set theory, mathematical logic, measure theory, algebra, and functional analysis. Nevertheless, to prove more robust and pivotal theorems, like Tychonoff’s theorem or the proposition that “every vector space has a basis”, the full strength of AC is necessary. This research also evaluated and contrasted the power of specific robust variants of AC, unearthing valuable outcomes when these potent axioms are implemented. Yet, adopting these strong axioms can considerably constrain the explorative capacity within the Zermelo-Fraenkel set theory with the Axiom of Choice (ZFC). For instance, it becomes impossible for large cardinals equal to or exceeding measurable cardinals to exist. Some scholars also contend that the axiom “V=L” curtails mathematical freedom, as it provides solutions to certain pivotal quandaries, such as the Continuum Hypothesis (GCH). Choosing a stance on these problems inevitably means renouncing the intriguing implications of the opposing perspective. The significance of this review is underscored by its in-depth examination of how both strong and weak variants of AC influence foundational mathematics and its various subbranches. While much of the existing research tends to discuss AC in isolated theoretical contexts, this study addresses a noticeable gap by providing a comprehensive review of the variants of this pivotal axiom within ZFC. Potential avenues for future investigations might include delving deeper into stronger or weaker variants of AC or its negation, reconfiguring the foundations of certain extant theories using weak AC variants, or seeking a potent axiom that not only confirms AC but also offers additional valuable insights, similar to the ongoing Ultimate-L program.
References
[1]. Bagaria, J. (2023, January 31). Set Theory (E. N. Zalta & U. Nodelman, Eds.). Stanford Encyclopedia of Philosophy.
[2]. L. Bell, J. (2021, December 10). The Axiom of Choice (E. N. Zalta, Ed.). Stanford Encyclopedia of Philosophy.
[3]. Khatchatourian, I. (2018). The Axiom of Choice. In University of Toronto (MAT327 11-Choice). University of Toronto Mathematics Department.
[4]. Herrlich, H. (2006). Axiom of Choice. In Springer eBooks (Vol. 1876). Springer.
[5]. nLab authors. (2023b, September). Axiom of Choice. nLab. https://ncatlab.org/nlab/ show/ axiom+ of+ choice.
[6]. Hrbacek, K., & Katz, M. G. (2021). Infinitesimal analysis without the Axiom of Choice. Annals of Pure and Applied Logic, 172(6), 102959.
[7]. Devlin, K. J. (1984). Constructibility. Springer.
[8]. Banach, S., & Tarski, A. (1924). Sur la décomposition des ensembles de points en parties respectivement congruentes. Fundamenta Mathematicae, 6, 244–277.
[9]. G. Levy, M. (2021, August 26). Banach-Tarski and the Paradox of Infinite cloning | Quanta Magazine. Quanta Magazine.
[10]. Wagley, M. (2012, June 3). Axiom of Choice, Trichotomy, and The Continuum Hypothesis. University of Washington Department of Mathematics.
[11]. Blass, A. (1984). Existence of bases implies the axiom of choice. Contemporary Mathematics, 31–33.
[12]. Bernays, P. (1942). A system of axiomatic set theory. Part III. Infinity and enumerability. Analysis. Journal of Symbolic Logic, 7(2), 65–89.
[13]. nLab authors. (2012, August 24). Entire relation. nLab. https://ncatlab.org/nlab/show/entire+relation.
[14]. nLab authors. (2023c, September). Dependent Choice. nLab. https://ncatlab.org/nlab/show/ dependent+choice.
[15]. Jech, T. J. (2008). The axiom of choice. Courier Corporation.
[16]. Howard, P. E., & Rubin, J. E. (1998). Consequences of the axiom of choice. In Mathematical surveys.
[17]. Keremedis, K. (2001). Disasters in topology without the axiom of choice. Archive for Mathematical Logic, 40(8), 569–580.
[18]. Jia, R. (2017, March 15). The axiom of choice in Topology. Union | Digital Works. https:/ /digitalworks. union.edu/theses/46/.
[19]. Koppelberg, S. (2011). Filters and ultrafilters. Freie Universitat Berlin Logik Und Mengenlehre.
[20]. Kirman, A., & Sondermann, D. (1972). Arrow’s theorem, many agents, and invisible dictators. Journal of Economic Theory, 5(2), 267–277.
[21]. nLab authors. (2021, June 14). Ultrafilter theorem. nLab. https://ncatlab.org/nlab/ show/ ultrafilter + theorem.
[22]. E. Caicedo, A. (2010, November 19). Is the statement that every field has an algebraic closure known to be equivalent to the ultrafilter lemma? MathOverflow.
[23]. Devlin, K. J. (1984). Constructibility. Springer.
[24]. Gödel, K. (1940). Consistency of the continuum hypothesis. (AM-3). In Princeton University Press eBooks.
[25]. Kechris, A. S. (1984). The axiom of determinacy implies dependent choices in L(R). Journal of Symbolic Logic, 49(1), 161–173.
[26]. Shelah, S. (1975). A compactness theorem for singular cardinals, free algebras, Whitehead problem and tranversals. Israel Journal of Mathematics, 21(4), 319–349. https://doi.org/10. 1007/ bf02757993.
[27]. Maddy, P. (2000). Naturalism in Mathematics. In Oxford University Press eBooks.
[28]. Hamkins, J. D. (2013). A MULTIVERSE PERSPECTIVE ON THE AXIOM OF CONSTRUCTIBILITY. In Lecture notes series, Institute For Mathematical Sciences, National University of Singapore (pp. 25–45).
[29]. Scott, D. (2003). Measurable cardinals and constructible sets. In CO-PUBLISHED WITH SINGAPORE UNIVERSITY PRESS eBooks (pp. 407–410). https://doi.org/ 10.1142/ 9789812564894_0020.
[30]. Woodin, H. (2021, January 13). “On the Mathematical Necessity of the Infinite” by Hugh Woodin [Video]. YouTube. https://www.youtube.com/watch?v=KI4yrWzRSWI.
[31]. Karagila, A. (2022, July 4). What are the motivations of large cardinal research? Mathematics Stack Exchange.
[32]. Hamkins, J. D. (2012). THE SET-THEORETIC MULTIVERSE. Review of Symbolic Logic, 5(3), 416–449.
[33]. Hamkins, J. D. (2015). Is the Dream Solution of the Continuum Hypothesis Attainable? Notre Dame Journal of Formal Logic, 56(1). https://doi.org/10.1215/00294527-2835047.
[34]. Sierpiński, W. (1934). Hypothèse du continu.
[35]. Stanton, S. (2010). The Axiom of Determinacy [Graduate School Dissertation]. Virginia Commonwealth University.
[36]. Shao, D. (2012). On Ramsey Property Under the Axiom of Determinacy [PhD thesis]. National University of Singapore.
[37]. Hamkins, J. D., & Gitman, V. (2011, December). Axiom of determinacy. Cantors-attic.
[38]. nLab authors. (2023c, September). Dependent Choice. nLab. https://ncatlab.org/nlab/ show/ dependent +choice
[39]. Lopez-Ortiz, A. (1998, February 23). Relevance of the axiom of choice. UWaterloo Computer Science.
[40]. Marfori, M. A. (2020). A new look at quine on set theory. In Oxford University Press eBooks (pp. 253–279).
[41]. Fan, C. (2010). Reverse Mathematics. UChicago Mathematics.
Cite this article
Wang,Y. (2023). Assessing the influence of the axiom of choice’s variations on mathematical foundations and subdisciplines. Theoretical and Natural Science,13,187-194.
Data availability
The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.
Disclaimer/Publisher's Note
The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
About volume
Volume title: Proceedings of the 3rd International Conference on Computing Innovation and Applied Physics
© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and
conditions of the Creative Commons Attribution (CC BY) license. Authors who
publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons
Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this
series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published
version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial
publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and
during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See
Open access policy for details).
References
[1]. Bagaria, J. (2023, January 31). Set Theory (E. N. Zalta & U. Nodelman, Eds.). Stanford Encyclopedia of Philosophy.
[2]. L. Bell, J. (2021, December 10). The Axiom of Choice (E. N. Zalta, Ed.). Stanford Encyclopedia of Philosophy.
[3]. Khatchatourian, I. (2018). The Axiom of Choice. In University of Toronto (MAT327 11-Choice). University of Toronto Mathematics Department.
[4]. Herrlich, H. (2006). Axiom of Choice. In Springer eBooks (Vol. 1876). Springer.
[5]. nLab authors. (2023b, September). Axiom of Choice. nLab. https://ncatlab.org/nlab/ show/ axiom+ of+ choice.
[6]. Hrbacek, K., & Katz, M. G. (2021). Infinitesimal analysis without the Axiom of Choice. Annals of Pure and Applied Logic, 172(6), 102959.
[7]. Devlin, K. J. (1984). Constructibility. Springer.
[8]. Banach, S., & Tarski, A. (1924). Sur la décomposition des ensembles de points en parties respectivement congruentes. Fundamenta Mathematicae, 6, 244–277.
[9]. G. Levy, M. (2021, August 26). Banach-Tarski and the Paradox of Infinite cloning | Quanta Magazine. Quanta Magazine.
[10]. Wagley, M. (2012, June 3). Axiom of Choice, Trichotomy, and The Continuum Hypothesis. University of Washington Department of Mathematics.
[11]. Blass, A. (1984). Existence of bases implies the axiom of choice. Contemporary Mathematics, 31–33.
[12]. Bernays, P. (1942). A system of axiomatic set theory. Part III. Infinity and enumerability. Analysis. Journal of Symbolic Logic, 7(2), 65–89.
[13]. nLab authors. (2012, August 24). Entire relation. nLab. https://ncatlab.org/nlab/show/entire+relation.
[14]. nLab authors. (2023c, September). Dependent Choice. nLab. https://ncatlab.org/nlab/show/ dependent+choice.
[15]. Jech, T. J. (2008). The axiom of choice. Courier Corporation.
[16]. Howard, P. E., & Rubin, J. E. (1998). Consequences of the axiom of choice. In Mathematical surveys.
[17]. Keremedis, K. (2001). Disasters in topology without the axiom of choice. Archive for Mathematical Logic, 40(8), 569–580.
[18]. Jia, R. (2017, March 15). The axiom of choice in Topology. Union | Digital Works. https:/ /digitalworks. union.edu/theses/46/.
[19]. Koppelberg, S. (2011). Filters and ultrafilters. Freie Universitat Berlin Logik Und Mengenlehre.
[20]. Kirman, A., & Sondermann, D. (1972). Arrow’s theorem, many agents, and invisible dictators. Journal of Economic Theory, 5(2), 267–277.
[21]. nLab authors. (2021, June 14). Ultrafilter theorem. nLab. https://ncatlab.org/nlab/ show/ ultrafilter + theorem.
[22]. E. Caicedo, A. (2010, November 19). Is the statement that every field has an algebraic closure known to be equivalent to the ultrafilter lemma? MathOverflow.
[23]. Devlin, K. J. (1984). Constructibility. Springer.
[24]. Gödel, K. (1940). Consistency of the continuum hypothesis. (AM-3). In Princeton University Press eBooks.
[25]. Kechris, A. S. (1984). The axiom of determinacy implies dependent choices in L(R). Journal of Symbolic Logic, 49(1), 161–173.
[26]. Shelah, S. (1975). A compactness theorem for singular cardinals, free algebras, Whitehead problem and tranversals. Israel Journal of Mathematics, 21(4), 319–349. https://doi.org/10. 1007/ bf02757993.
[27]. Maddy, P. (2000). Naturalism in Mathematics. In Oxford University Press eBooks.
[28]. Hamkins, J. D. (2013). A MULTIVERSE PERSPECTIVE ON THE AXIOM OF CONSTRUCTIBILITY. In Lecture notes series, Institute For Mathematical Sciences, National University of Singapore (pp. 25–45).
[29]. Scott, D. (2003). Measurable cardinals and constructible sets. In CO-PUBLISHED WITH SINGAPORE UNIVERSITY PRESS eBooks (pp. 407–410). https://doi.org/ 10.1142/ 9789812564894_0020.
[30]. Woodin, H. (2021, January 13). “On the Mathematical Necessity of the Infinite” by Hugh Woodin [Video]. YouTube. https://www.youtube.com/watch?v=KI4yrWzRSWI.
[31]. Karagila, A. (2022, July 4). What are the motivations of large cardinal research? Mathematics Stack Exchange.
[32]. Hamkins, J. D. (2012). THE SET-THEORETIC MULTIVERSE. Review of Symbolic Logic, 5(3), 416–449.
[33]. Hamkins, J. D. (2015). Is the Dream Solution of the Continuum Hypothesis Attainable? Notre Dame Journal of Formal Logic, 56(1). https://doi.org/10.1215/00294527-2835047.
[34]. Sierpiński, W. (1934). Hypothèse du continu.
[35]. Stanton, S. (2010). The Axiom of Determinacy [Graduate School Dissertation]. Virginia Commonwealth University.
[36]. Shao, D. (2012). On Ramsey Property Under the Axiom of Determinacy [PhD thesis]. National University of Singapore.
[37]. Hamkins, J. D., & Gitman, V. (2011, December). Axiom of determinacy. Cantors-attic.
[38]. nLab authors. (2023c, September). Dependent Choice. nLab. https://ncatlab.org/nlab/ show/ dependent +choice
[39]. Lopez-Ortiz, A. (1998, February 23). Relevance of the axiom of choice. UWaterloo Computer Science.
[40]. Marfori, M. A. (2020). A new look at quine on set theory. In Oxford University Press eBooks (pp. 253–279).
[41]. Fan, C. (2010). Reverse Mathematics. UChicago Mathematics.