1. Introduction
Advanced Encryption Standard (AES) is a modern encryption scheme widely used in different fields [1-3]. Systems build according to this standard are considered as safe in light of the today’s maximum computing power. The system can be considered as a series of algorithms that keep adding complexity and chaoticity to the original plain text. One can thinking about it as always shuffling a deck in a same way, and if the shuffle algorithm is unknown, it will be extremely hard to recover the original cards order from the deck after shuffling. However, once the receivers know the way how the deck shuffled, which is the key text, they can decrypt the cyphertext by reverse the processes of shuffling. The encryption algorithms usually involve operations like finding multiplicative inverse in Galois Field (GF) [4], mixing data in different columns, and adding random data chunk to the plaintext during encrypting. However, in this passage, the only operation we care is the XOR bit operation between the encrypted text and the key text. The reason of that is because in the worst scenario, the attackers would know exactly how the encryption system work, and to build a perfectly safe scheme, it is important to ensure that the attackers would not be able to break the system with the knowledge about the system as long as they do not have the key. In other words, if the key is secret, then the system is safe. However, if one can gain knowledge about the key by certain method, the system will suddenly break down. The original passage has introduced few models to do this, and in this paper, logistic regression is the model chosen to perform the same trail in the original paper.
As discussed above, AES is considered safe in the most modern scenarios, but this conclusion can be reached only in the ideal world, or in other words, if we only consider the algorithm aspect. However, in the real world, a most powerful and inevitable attacking method called Side-Channel Analysis (SCA) [5-7] can break a system without any knowledge about the encryption algorithm. SCA only gain knowledge from the information leakage from real-world implementation. That is, for example, responding time of the system, how much memory or computing power is used in a time period, or in this paper, the electronic radiation emitted by the architecture during the encryption. Analysis of such information leakage is how SCA work. Since one can never prevent attacker from obtaining such information, and it is almost impossible to avoid leakage in such way, SCA is considered as the strongest attacking tool in modern crypto world.
The original paper has shown that a trained AI models can perform very well when cracking the encryption system. However, they also found that those models can be strongly affected by the noise. In this paper, results show that logistic regression model might be a better way to deal with noise. This model might be a more powerful tool for attacker, and the results lead to a better understanding of how to improve the security level for encryption hardware when facing AI attack [8,9].
The following paragraphs firstly introduce the ANSSI SCA Database (ASCAD) dataset [10] with the general methodology for performance evaluation. After that, the experiment results will be represented in the order of regular model, different activation function, and different optimizer. Some observation and conclusions can be derived from them. Finally, the paper will talk about the speculation and future problems.
2. Method
2.1. ASCAD dataset
ASCAD is a system built by the original researchers. This system provides a benchmark for developing and testing artificial intelligence (AI) models against encryption. The system contains two parts of data and three major functions.
The first part of database contains raw data draw from an encryption architecture called ATMega8515. While encrypting, the electromagnetic radiation was recorded by the original team, and 60,000 out of 100,000 traces were selected to fill the database. The recorded radiation has been proved to be related with one operation during the encrypting process by observing the signal-to-noise rate (SNR) by the team. The operation is XOR of two 8-bits segments: one from the plaintext and another from the key text. The goal for the models is trying to infer the key text k, which is an 8-bits string. If the model can successfully guess the key text k, this means it would be able to, as previously stated, bypass all the information of plaintext, ciphertext, and the encryption system and directly crack the whole scheme.
The second part is the trained model provide by the team, and some of them performs perfectly when sufficient amount of data is given. There are three functions provided in the system: extracting data, training, and testing. These functions allow anyone to train and test their own models on random data extract from the original database. Moreover, the extracted data are random each time, and ASCAD will automatically and randomly add desynchronizations to the selected data to form different training and testing sets.
2.2. Ranking function and benchmarks
The ranking function will output a series of all 8-bits numbers in a decreasing order of the possibilities that the model believe that the number is the real key. Therefore, the length of output will always be 256 as there are total of 256 8-bits numbers, and the most possible one the model infer is at index 0. Moreover, the results are evaluated by t-fold cross-validation, and the original group choose t equals to 10. This ensure that the results generated by the ASCAD system are unbiased and accurate but still saving computing power.
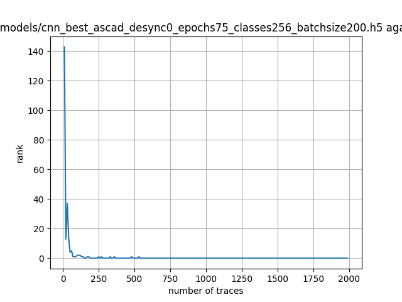
Figure 1 shows a standard output of the ASCAD database.
|
Figure 1. A standard output of the ASCAD dataset. |
This result is generated from a trained CNN model provided by the database. The left bar is the position of real key in the output of the ranking function. The bottom bar is the number of traces given to the model. As one can see, this model actually performs very well as the ranking of the key almost always stay at zero after about 200 traces were given.
2.3. Multinomial logistic regression
Logistic regression is a model to perform regression based on multiple input characteristics: \( X=\lbrace {x_{1}},{x_{2}}, …, {x_{m}}\rbrace \) . The model tries to return the best guess of input data: \( Y={[{y_{1}} {y_{2}}…{y_{n}}]^{T}} \) for a set of training data. Here, \( {y_{k}} \) represents the probability that the model believes the training data falls in the kth category, \( {y_{k}} \) . In the binomial logistic regression scenario, \( {y_{k}} \) can be computed as:
\( {y_{k}}=g({a_{k}})=\frac{1}{1+{e^{-a}}} \) (1)
where \( g(a) \) is the activation function and
\( {a_{k}}=\sum _{i=0}^{m}{w_{i}}{x_{ik}} \) (2)
However, since the output has 256 categories, we need to derive the formula for multinomial logistic regression. Note that one can consider this problem as choosing one outcome from 255 independent binary regression models. Then, if we assume the chosen one is the last category, n, for each model:
\( ln{\frac{{y_{k}}}{{y_{n}}}}={w_{k}}{x_{N}} \) (3)
Where \( {x_{N}} \) denotes the characteristic vector for last input data. Then, one can take the exponential both sides:
\( {y_{k}}={y_{n}}{e^{{w_{k}}{x_{N}}}} \) (4)
Since sum of possibilities of all categories is 1, we have:
\( {y_{n}}=1-\sum _{j=0}^{n-1}{y_{j}}=1-\sum _{j=0}^{n-1}{y_{n}}{e^{{w_{j}}{x_{N}}}} \) (5)
We get:
\( {y_{n}}=\frac{1}{1+\sum _{j=1}^{n-1}{e^{{w_{j}}{x_{N}}}}} \) (6)
And thus,
\( {y_{k}}=\frac{{e^{{w_{k}}{x_{N}}}}}{1+\sum _{j=1}^{n-1}{e^{{w_{j}}{x_{N}}}}} \) (7)
Where \( {w_{n}}=0 \) .
Then, in order to optimize the model, two optimizers were selected: root mean square propagation (RMSprop) and Stochastic gradient descent (SGD). They are both based on gradient descent, but the former one has a lower speed of descent than the latter one. Comparing the results of two cases might provide some speculation of features about the objective function. Moreover, instead of using multinomial logistic regression, ReLU is used as activation function in the first section of the experiment, and this is because ReLU is used by the original team.
2.4. Desynchronization
In a real-world situation, the electronic radiation emitted by the encryption architecture can often be interfered by many different factors. Those will eventually lead to the unstableness of the data measured. Jitters, meaning that the real signal will reach earlier or later than expected, will often show up in any electronic device. However, this signal deviation will severely affect the performance of the model. In the database, desynchronization is produced by randomly shifting each bit by the upper bound of the desync parameter, which is either 50 or 100. Since they are randomly generated by the algorithm, we can assume the noise conform to a Gaussian distribution around the true value. Therefore, minimizing the cross-entropy error as the original group did by logistic regression model is a reasonable way to perform the experiment. In the original passage, Both CNN and MLP trained for different desynchronization did not perform as well as before, especially when facing larger desynchronization.
3. Result
This passage aims to find the relations between the parameter and the performance of the logistic regression model, and comparing them with others. The parameters are batch size, desynchronization, activation function, and optimizer. Firstly, three different model were tested, each of them has 40 epochs but different activation (3.2) function or optimizer (3.3). In each case, the model is tested with different batch sizes and different desynchronization. By analyzing the results, some general conclusions can be drawn.
3.1. Regular logistic regression
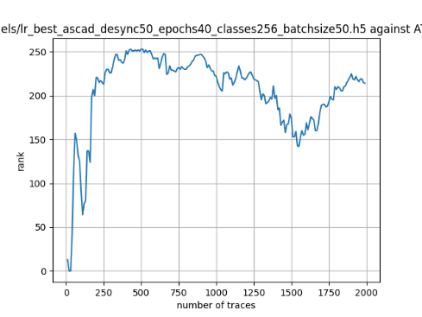
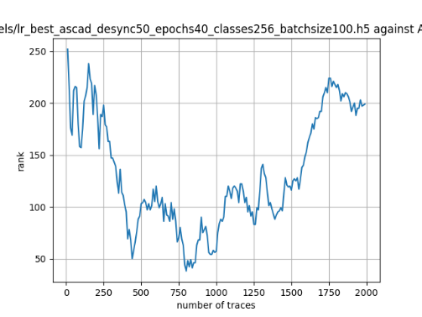
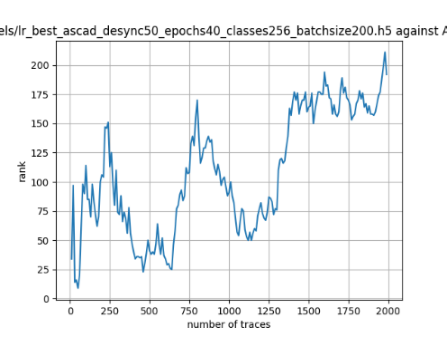
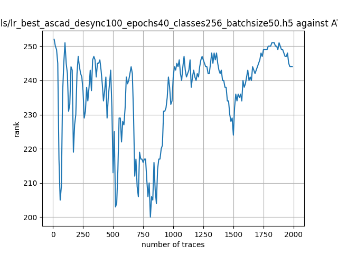
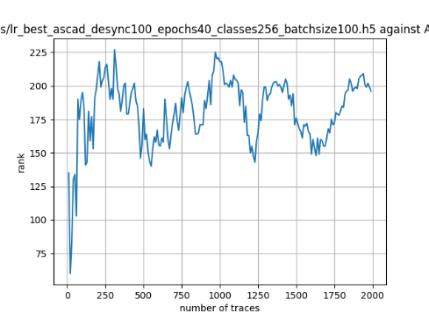
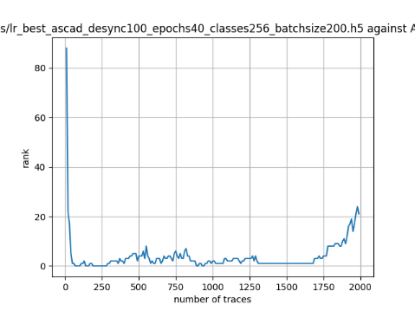
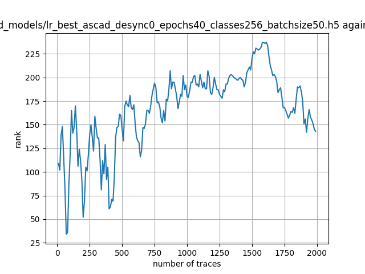
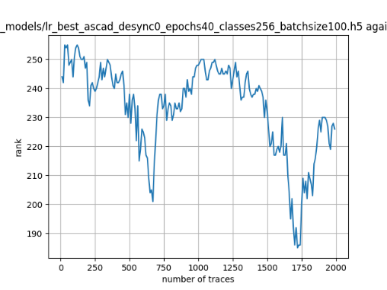
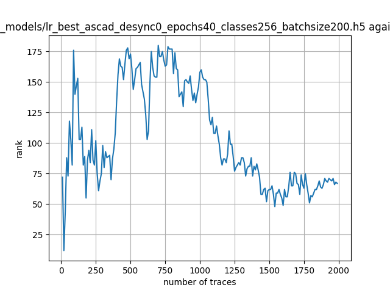
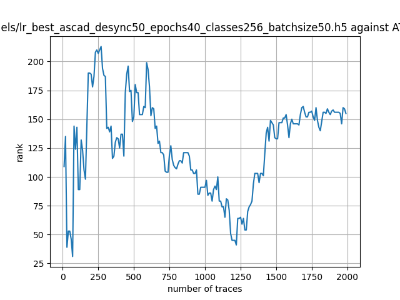
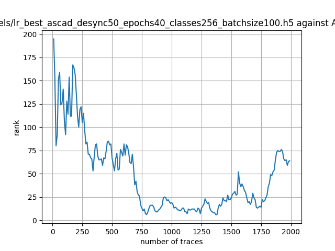
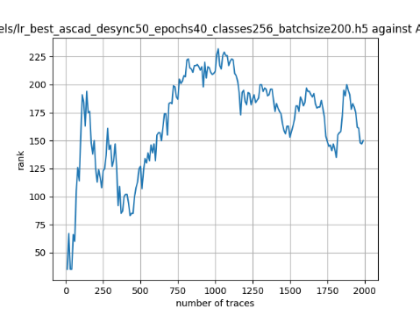
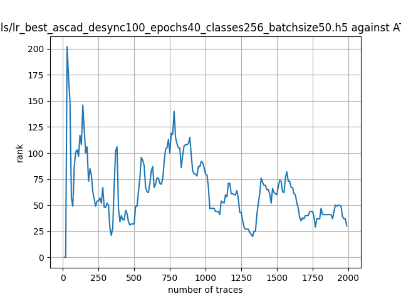
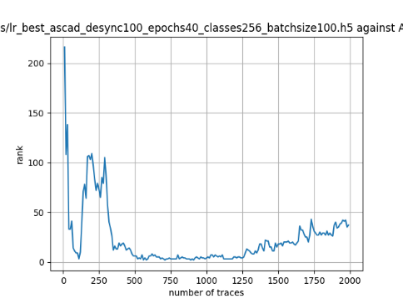
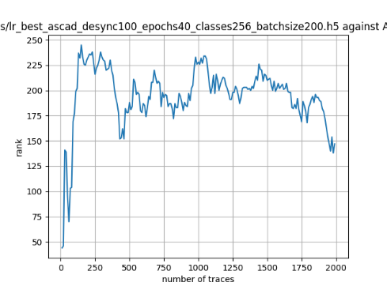
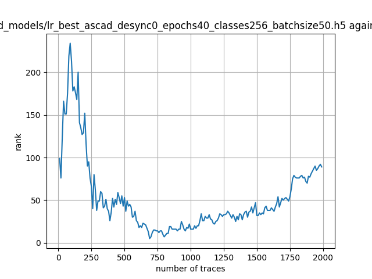
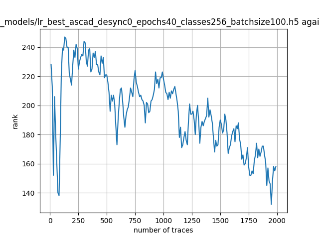
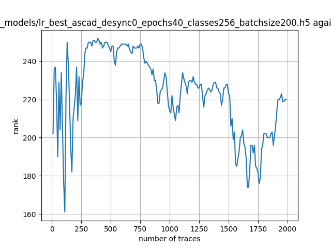
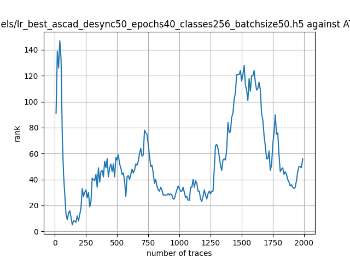
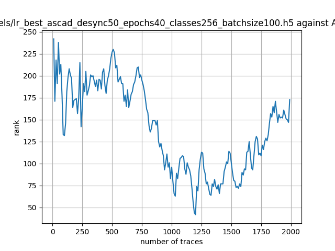
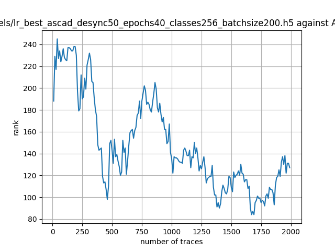
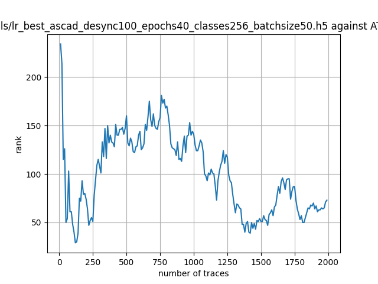
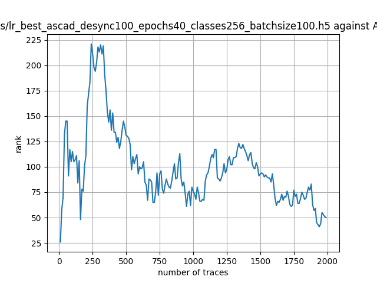
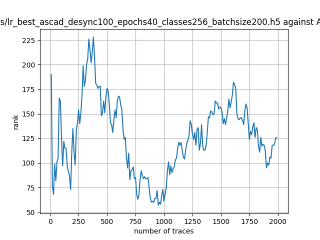
In this case, the activation function is ReLU and the optimizer is RMSprop. Regular logistic regression performs bad in all cases except for the last one. What noteworthy is that this case has the most desynchronization, and all the models trained by the original authors with different hyperparameters did not perform well in this circumstance. Performances achieved from different hyper-parameter combinations are demonstrated in Figure 2, Figure 3 and Figure 4.
|
|
|
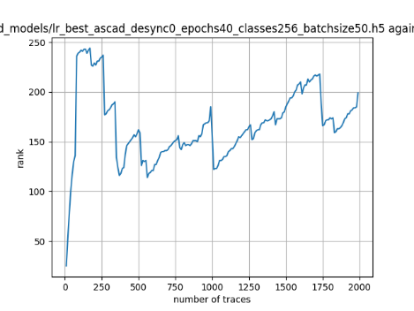
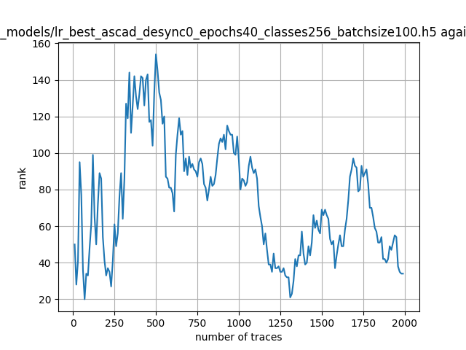
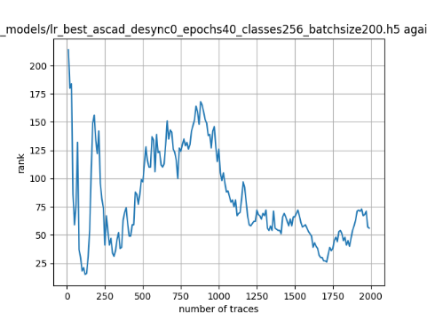
Figure 2. Results with 0 desynchronization. The batch sizes from left to right are 50, 100, 200 respectively. | ||
|
|
|
Figure 3. Results with 50 desynchronization. The batch sizes from left to right are 50, 100, 200 respectively. | ||
|
|
|
Figure 4. Results with 100 desynchronization. The batch sizes from left to right are 50, 100, 200 respectively. | ||
Also, compare figures from right side to the left, one can conclude that the larger batch size for this model generally performs better than smaller size, and this shows that it is hard for the model to extract information from small amount of sample data in one epoch. The best result is the last result in Figure 4, which is generated with 100 desynchronization and batch size 200, and the ranking of the target is closed to 0 when less than 1750 traces were given. While models in the original paper cannot reach ranking below even when 5000 traces are given. However, results of other groups are very unstable, which might show that the model quickly become overfitting if the batch size is too small.
3.2. Change activation function to sigmoid
In this case, the activation function is sigmoid and the optimizer is RMSprop. The model does not perform well after changing its activation function to sigmoid. However, we can still observe that it performs better than the original paper when the desynchronization is relatively high with batch size 100. Performances are demonstrated in Figure 5, Figure 6 and Figure 7.
|
|
|
Figure 5. Results using Sigmoid activation function with 0 desynchronization. The batch sizes from left to right are 50, 100, 200 respectively. | ||
|
|
|
Figure 6. Results using Sigmoid activation function with 50 desynchronization. The batch sizes from left to right are 50, 100, 200 respectively. | ||
|
|
|
Figure 7. Results using Sigmoid activation function with 100 desynchronization. The batch sizes from left to right are 50, 100, 200 respectively. | ||
The best performance in the middle graph of figure 7 is generated with 100 desynchronization and batch size 100. Unlike ReLU regression, the multinomial logistic regression prefers batch size 100. However, when there are no desynchronizations, the performance is relatively bad, and the higher desynchronizations lead to a better performance when batch size is 100. This results also show that the logistic regression model has the ability to extract useful information from a highly noisy environment.
3.3. Change optimizer to SGD
In this case, the activation function is ReLU and the optimizer is SGD. The model never performs well, so SGD is not appropriate for such classification problem. Performances are demonstrated in Figure 8, Figure 9 and Figure 10.
|
|
|
Figure 8. Results using SGD optimizer with 0 desynchronization. The batch sizes from left to right are 50, 100, 200 respectively. | ||
|
|
|
Figure 9. Results using SGD optimizer with 50 desynchronization. The batch sizes from left to right are 50, 100, 200 respectively. | ||
|
|
|
Figure 10. Results using SGD optimizer with 100 desynchronization. The batch sizes from left to right are 50, 100, 200 respectively. | ||
The results are highly unstable. Comparing with the model using RMSprop, these results show that it is hard to train the regression model with SDG. One possible reason is that SDG will go downhill overly fast in this scenario, and the objective function has a rugged surface. Therefore, SDG could not find the optimal point, but it can only traverse randomly upon the surface.
4. Discussion
Logistic regression performs not well in the most of cases. Some speculations were made based on the observation. However, it remains unclear why the performance varies and becomes unpredictable in most of cases. Moreover, there is also no firm theoretical bases to explain how AI models have those behaviours and performance in the different circumstances. In other words, the way how AI attacking the AES system is remain unknown. Most importantly, how could the encryption device be improved based on the results of attacking by AI models. Some possible methods could be using blinding techniques that turn the input and output data into unpredictable states or adding redundant random chunks with key text or encrypted plain text. Once the information leakage become unpredictable, there would be no useful features or information for AI models to extract.
5. Conclusion
Generally, the batch sizes can sometimes affect the result. For the first two model, some particular batch sizes could be preferred. Logistic regression can sometimes handle desynchronization decently but still perform worse than MLP and CNN mentioned in the original passage in the most of the time. The reason of this might be that the logistic regression model can be easily overfitted, but if it deals with deviated data or noise, it can do much better with extracting valuable features than those from original team. Moreover, in almost all cases, there is a sharp decreasing when the first few traces are given, and after that, the performance start to getting unpredictable. Those sharp decreasing shows that the model might be well-trained at first but quickly become overfitting. In conclusion, logistic regression is easy to train and can sometimes be considered as an alternative method for SCA analysis. However, it does not perform robustly in the environment given above.
References
[1]. Bellare, M., & Rogaway, P. (2005). Introduction to modern cryptography. Ucsd Cse, 207, 207.
[2]. Zhang, X., & Parhi, K. K. (2002). Implementation approaches for the advanced encryption standard algorithm. IEEE Circuits and systems Magazine, 2(4), 24-46.
[3]. Daemen, J., & Rijmen, V. (2001). Reijndael: The advanced encryption standard. Dr. Dobb's Journal: Software Tools for the Professional Programmer, 26(3), 137-139.
[4]. Carlitz, L. (1932). The arithmetic of polynomials in a Galois field. American Journal of Mathematics, 54(1), 39-50.
[5]. Hospodar, G., Gierlichs, B., De Mulder, E., Verbauwhede, I., & Vandewalle, J. (2011). Machine learning in side-channel analysis: a first study. Journal of Cryptographic Engineering, 1(4), 293-302.
[6]. Masure, L., Dumas, C., & Prouff, E. (2020). A comprehensive study of deep learning for side-channel analysis. IACR Transactions on Cryptographic Hardware and Embedded Systems, 348-375.
[7]. Secure-IC, S. A. S., & Cesson-Sévigné, F. (2022). Profiled Side-Channel Analysis in the Efficient Attacker Framework. In Smart Card Research and Advanced Applications: 20th International Conference, CARDIS 2021, 13173, 44.
[8]. Falco, G., Viswanathan, A., Caldera, C., & Shrobe, H. (2018). A master attack methodology for an AI-based automated attack planner for smart cities. IEEE Access, 6, 48360-48373.
[9]. Chen, T., Liu, J., Xiang, Y., Niu, W., Tong, E., & Han, Z. (2019). Adversarial attack and defense in reinforcement learning-from AI security view. Cybersecurity, 2(1), 1-22.
[10]. Benadjila, R., Prouff, E., Strullu, R., Cagli, E., & Dumas, C. (2020). Deep learning for side-channel analysis and introduction to ASCAD database. Journal of Cryptographic Engineering, 10(2), 163-188.
Cite this article
Liao,T. (2023). Logistic regression-based side-channel analysis attacks. Theoretical and Natural Science,18,216-223.
Data availability
The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.
Disclaimer/Publisher's Note
The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
About volume
Volume title: Proceedings of the 2nd International Conference on Computing Innovation and Applied Physics
© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and
conditions of the Creative Commons Attribution (CC BY) license. Authors who
publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons
Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this
series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published
version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial
publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and
during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See
Open access policy for details).
References
[1]. Bellare, M., & Rogaway, P. (2005). Introduction to modern cryptography. Ucsd Cse, 207, 207.
[2]. Zhang, X., & Parhi, K. K. (2002). Implementation approaches for the advanced encryption standard algorithm. IEEE Circuits and systems Magazine, 2(4), 24-46.
[3]. Daemen, J., & Rijmen, V. (2001). Reijndael: The advanced encryption standard. Dr. Dobb's Journal: Software Tools for the Professional Programmer, 26(3), 137-139.
[4]. Carlitz, L. (1932). The arithmetic of polynomials in a Galois field. American Journal of Mathematics, 54(1), 39-50.
[5]. Hospodar, G., Gierlichs, B., De Mulder, E., Verbauwhede, I., & Vandewalle, J. (2011). Machine learning in side-channel analysis: a first study. Journal of Cryptographic Engineering, 1(4), 293-302.
[6]. Masure, L., Dumas, C., & Prouff, E. (2020). A comprehensive study of deep learning for side-channel analysis. IACR Transactions on Cryptographic Hardware and Embedded Systems, 348-375.
[7]. Secure-IC, S. A. S., & Cesson-Sévigné, F. (2022). Profiled Side-Channel Analysis in the Efficient Attacker Framework. In Smart Card Research and Advanced Applications: 20th International Conference, CARDIS 2021, 13173, 44.
[8]. Falco, G., Viswanathan, A., Caldera, C., & Shrobe, H. (2018). A master attack methodology for an AI-based automated attack planner for smart cities. IEEE Access, 6, 48360-48373.
[9]. Chen, T., Liu, J., Xiang, Y., Niu, W., Tong, E., & Han, Z. (2019). Adversarial attack and defense in reinforcement learning-from AI security view. Cybersecurity, 2(1), 1-22.
[10]. Benadjila, R., Prouff, E., Strullu, R., Cagli, E., & Dumas, C. (2020). Deep learning for side-channel analysis and introduction to ASCAD database. Journal of Cryptographic Engineering, 10(2), 163-188.