1. Introduction

Two-dimensional quantum materials represent a novel class of materials with unparalleled properties and potential applications. This is due to their distinct two-dimensional structure, which allows electrons to move freely only in two dimensions at a non-nanometer scale, and the other dimension is limited within the atom scale. The inception of research in this area can be traced back to the discovery of graphene in 2004. As a two-dimensional (2D) carbon-based material, graphene boasts exceptional electrical conductivity, thermal stability, and mechanical strength [1]. The research on graphene reveals the nature of 2D quantum materials while stimulating the research on 2D materials beyond carbon. The ingredients and structures of two-dimensional materials beyond carbon are diverse [1], elemental 2D materials, boron nitride, gallium nitride, transitional metal dichalcogenides (TMDs), and other materials are continuously designed and synthesized. The wide range of ingredients and structures available in 2D materials beyond carbon offer excellent properties and applications, including superconductivity, ferromagnetism, antiferromagnetism, quantum spin liquid (QSL), Hall effect, and more. They are widely utilized in the research and production of new energy and information function devices [1]. Additionally, some 2D materials hold significant importance in the medical field [2]. 2D materials beyond carbon develop rapidly, featuring diverse structures, excellent properties, and a wide range of applications. This type of material needs to be summarized and revisited to enable further research, which is why the article was written.

This article provides an in-depth analysis of the properties and applications of 2D materials beyond carbon, focusing on excellent properties including superconductivity, ferromagnetism, antiferromagnetism, and QSL phase. After introducing the phenomenon and production mechanism of each property, the author then explores application prospects in conjunction with specific cases. Finally, a summary and outlook are given. The article is written for providing some reference and inspiring innovations for the research in related fields of materials science.

2. Superconductivity

Superconductivity is a fascinating phenomenon in solid-state physics, occurring in certain materials when, after undergoing a drop through a critical temperature T_c, the resistance of the material suddenly drops to zero. This phenomenon was first observed by Heike Kamerlingh Onnes in 1911, who found that when the mercury temperature was lowered to about 4.2K, its resistance vanished. Superconductors exhibit zero resistivity and the Meissner effect [3]. Below the critical temperature, the direct current resistance of a superconductor is zero, meaning that current can flow through it without dissipation. Superconductors in their superconducting state will expel magnetic fields, magnetic flux cannot penetrate the superconductor.

2.1. BCS Theory

The BCS theory offers a microscopic explanation for the superconducting properties of conventional superconductors and is attributed to the pioneering work of Bardeen, Cooper, and Schrieffer (BCS). First introduced in 1957, the theory seeks to elucidate the behaviour of electrons within these materials [3]. Furthermore, it provides insight into why they demonstrate zero electrical resistance and repel magnetic fields when the temperature falls below a critical value, represented as T_c [3].

Based on the BCS theory, Cooper pairs, or pairs of electrons, can form under certain conditions. Normally, electrons repel each other due to Coulomb forces. However, when their energy difference is less than the phonon energy, they can be attracted to each other through the exchange of virtual phonons. This attraction can overcome the Coulomb repulsion, resulting in a net attraction between the electrons [4]. At this point, two electrons with opposite momentum and spin can form a Cooper pair \( (k↑, -k↓) \) [4]. This lowers the energy of the electronic ground state, allowing single electrons at the Fermi energy to condense into a state with lower energy, called the BCS energy gap (Δ). It takes a minimum of 2Δ of energy to break the Cooper pairs and form an excited state. At low temperatures, all Cooper pairs can be condensed into the ground state, resulting in BEC condensation [4]. This ensures that electrons are not scattered during transport and results in the absence of electrical resistance.

According to the aforementioned model, BCS theory determines the superconducting transition temperature, \( {T_{c}} \) , in the weak coupling limit as per the following equation:

\( {T_{c}}=1.14{Θ_{D}}{e^{-\frac{1}{{N_{s}}(0)V}}}\ \ \ (1) \)

Here, \( {Θ_{D}} \) denotes the Debye temperature and \( {N_{s}}(0) \) represents the density of single-spin states for conducting electrons at the Fermi energy [4].

According to BCS theory, superconductivity is a macroscopic quantum effect that can explain various properties such as energy gaps, isotopic effects, and the Meissner effect. Superconductors that adhere to BCS theory are referred to as conventional or s-wave superconductors. Among the well-known conventional superconductors are aluminium, lead, and magnesium diboride (MgB₂). At 1.2K, aluminium can become a superconductor and showcase a robust Meissner effect. Even in very thin forms, conventional superconductors, such as aluminium, continue to exhibit superconductivity. Molecular Beam Epitaxy technology can be used to create aluminium thin films on appropriate substrates to examine its superconducting characteristics in a 2D limit [5].

2.2. Unconventional Superconductivity

According to the BCS theory, a maximal threshold exists for the critical temperature of superconductors, known as the McMillan limit, which stands at approximately 40K. Nonetheless, this theoretical framework has its constraints and falls short of accounting for the intricacies of non-conventional superconductors. Superconductors with critical temperatures surpassing the McMillan limit are classified as high-temperature superconductors, primarily encompassing copper-based and iron-based superconductors.

Research into copper-based superconductors has a rich history spanning nearly three decades. In 1986, Alex Müller and K. Alex Müller made a groundbreaking discovery regarding the La-Ba-Cu-O system. Its critical temperature was approximately 35K, representing as a significant improvement over previous superconductors [6]. The following year, C.W. Chu and their colleagues uncovered that the Y-Ba-Cu-O system was the first material to exhibit superconductivity above the temperature of liquid nitrogen (77K) [6]. In 1994, the critical temperature of the Hg-Ba-Ca-Cu-O system reached a staggering 164K. Copper-based superconductors, including YBCO (YBa₂Cu₃O₇) and BSCCO (Bi₂Sr₂CaCu₂O_8+x), boast a unique layered crystal structure, with copper-oxygen planes separated by other ionic layers [6]. This exceptional structure allows these materials to be exfoliated or deposited as atomic or single molecular layers, forming 2D materials.

In recent years, there have been exciting discoveries in the field of iron-based superconductors. Back in 2008, H. Hsono and their team found superconductivity in the F-doped La-Fe-As-O system at 26K. Since then, researchers have uncovered superconducting phenomena in other iron-based compounds like \( BaF{e_{2}}A{s_{2}} \) and FeSe. In fact, around 2012, there was a surge of interest in 2D iron-based superconductors, and there have been some significant breakthroughs since then. For instance, it was discovered that FeSe thin films exhibit high superconducting transition temperatures on SrTiO₃ substrates [7]. The team led by Q.-Y. Wang found that when a layer of FeSe thin film is grown on a SrTiO₃ substrate, the superconducting transition temperature of this system can exceed 109K [7]. This is remarkable because it’s much higher than the superconducting transition temperature of bulk FeSe, which is only about 8K. In fact, this is the highest reported T_c for iron-based superconductors to date. It is worth noting that the thickness of FeSe thin films plays a significant role in their superconducting properties, and 2D effects are crucial to these systems. All of these exciting developments make 2D iron-based superconductors an area of great interest in the fields of quantum computing and nanoelectronics technology.

Ising superconductivity is widely found in thin layers of TMDs. These materials exhibit a superconducting phenomenon under a strong magnetic field in a specific direction. TMDs have a honeycomb lattice structure like graphene, but differences in nearby atoms break the in-plane inversion symmetry. Breaking the symmetry of TMDs causes strong spin-orbit coupling (SOC), resulting in a polarization of the electron spin in the out-of-plane direction [8]. Electron spin direction is fixed, making them resistant to parallel external magnetic fields. Because of that, TMDs maintain superconductivity even under high magnetic fields, unlike traditional superconductors that lose it beyond a limit. Ising superconductivity is a fascinating and novel phenomenon, offering exciting possibilities for exploring and manipulating quantum states of matter under extreme conditions. It holds potential for use in quantum computing and spintronics, as it facilitates the creation and manipulation of unique quasiparticles like Majorana fermions and skyrmions [8].

In summary, two-dimensional materials are widely used in the research of superconductors. Whether it is traditional superconductors, iron-based superconductors, copper-based superconductors or Ising superconductors, 2D materials can be found.

3. Ferromagnetism and Antiferromagnetism

It is fascinating to note that some 2D materials showcase quantum properties that can manifest as magnetism. Certain 2D materials, such as VCl₃, VI₃, Fe₂Si, MnGeSe₃, and MnGeTe₃, exhibit ferromagnetism. The atoms and ions within the material align with an external magnetic field, thereby generating a net magnetization that persists even after the field is removed. Ferromagnetism in 2D materials arises from their magnetic anisotropy, allowing them to exhibit inherent ferromagnetism by overcoming thermal fluctuations [9]. Conversely, antiferromagnetism involves the magnetic moments of atoms and ions arranging themselves in the opposite direction of the magnetic field, resulting in zero magnetization on a macroscopic level. Magnetism and antiferromagnetism are two different magnetic phases exhibited by materials, characterized by differences in magnetic moment arrangement and behaviour.

Chromium triiodide (CrI₃) is a fascinating 2D material composed of chromium and iodine. Its hexagonal symmetry structure can be observed in Figure 1. Each chromium atom is surrounded by six iodine atoms forming an octahedral coordination. The material has been extensively studied due to its unique ferromagnetic and antiferromagnetic properties, which can be influenced by a range of factors such as temperature, pressure, layer numbers, and twist.

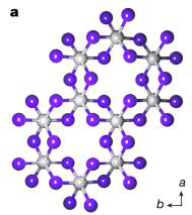
Figure 1. Structure of CrI₃ [10]

When CrI₃ is in its monolayer form, it behaves as a ferromagnet with a Curie temperature of around 45 K [11]. Each chromium atom of CrI₃ has three \( d \) orbital electrons participating in the formation of covalent bonds with iodine atoms, and the remaining two \( d \) orbital electrons keep their spins parallel to form local magnetic moments. These magnetic moments are between adjacent chromium atoms. The interaction causes them to tend to align in the same direction, resulting in ferromagnetism [12]. However, in its bilayer form, it exhibits antiferromagnetism where each layer retains its ferromagnetic properties, but antiferromagnetic coupling led by interlayer exchange interaction between different layers occurs. This results in a decrease or disappearance of the magnetic intensity and a shift in magnetic property [11].

Additionally, bilayer CrI₃ transitions from a ferromagnetic state to an antiferromagnetic state when subjected to strain. This is due to the effect of atomic orbitals and the electronic structure of Cr and I, altering interlayer interactions [12]. The transformation of magnetism makes CrI₃ an excellent material for studying 2D magnetic systems. Meanwhile, the magnetic coupling between different layers could be valuable for qubit research. The manipulation and control of magnetism may be used for quantum information processing and storage, providing a new physical platform for quantum computing. In addition to CrI₃, certain parallel-stacked bilayer TMDs exhibit ferromagnetism [13].

In summary, ferromagnetism and antiferromagnetism are two different magnetic phases exhibited by some 2D materials. The study of these phenomena is vital in the development of new materials with unique magnetic properties and applications in various fields such as electronics, spintronics, and quantum computing.

4. Quantum Spin Liquid

Certain 2D materials exhibit a fascinating phenomenon called QSL. It is a type of disorderly quantum state where spins are highly entangled. The QSL state doesn’t exhibit long-range magnetic order, nor does it spontaneously break lattice translation and rotation symmetry in macroscopic ferromagnetic systems, even at zero degrees Kelvin [14]. Unlike in traditional magnetic materials, where electrons spin gradually order as the temperature drops, QSL cannot form magnetic order at absolute zero. Consider a paramagnetic state with no interaction between spins as gas and a magnetically ordered state as solid. QSL falls in between, featuring strong interactions between spins but without exhibiting long-range magnetic order.

4.1. Frustration

Long-range disorders of spin liquids are caused by frustration. When certain geometric structures or competing interactions are present, the system cannot attain its lowest energy state, resulting in various degenerate states. In classical spin liquids, the degeneracy of the classical ground state exponentially increases with the system size when spin is on specific lattices, surpassing the degeneracy caused by ordinary spontaneous symmetry breaking, leading to magnetic disorder. For QSLs, the uncertainty principle must be considered, where the three components of spin operators adhere to the principle and demonstrate strong quantum fluctuation effects [14]. Smaller quantum numbers lead to more robust quantum fluctuations. In macroscopic systems, the competition between spontaneous spin order formation and quantum fluctuations results in a state characterized by long-range disorder.

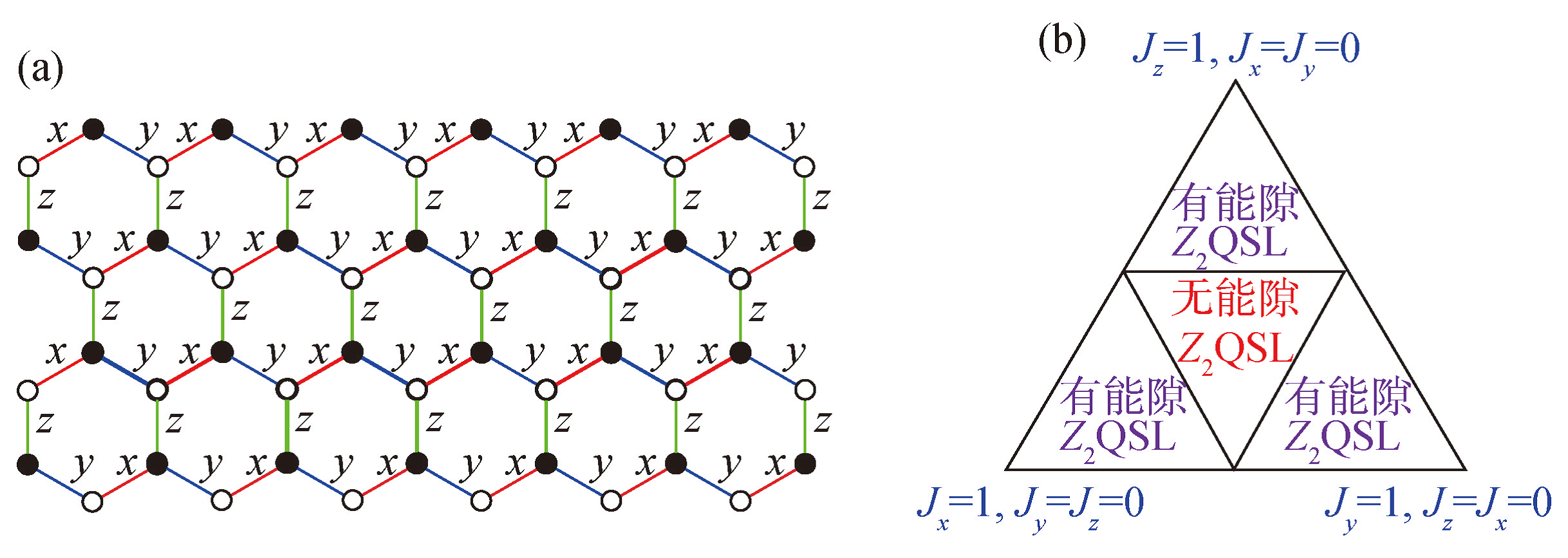
Figure 2. Schematic diagram of Kitaev model [15]

4.2. Kitaev Model

The Kitaev model defined on a 2D hexagonal lattice with effective spin-1/2, is used to describe QSLs. The core of the model lies in the strong anisotropy of the Ising-type of the spins along different lattice directions, which results in quantum frustration for spin [15]. As shown in Figure 2, the interactions along the x, y, and z directions only consider the Ising coupling for spins aligned along each direction. The Hamiltonian of the system can be expressed as

\( H={K_{x}}\sum _{x-bonds}S_{i}^{x}S_{j}^{x}+{K_{y}}\sum _{y-bonds}S_{i}^{y}S_{j}^{y}+{K_{z}}\sum _{z-bonds}S_{i}^{z}S_{j}^{z}\ \ \ (2) \)

where \( {K_{x}} \) , \( {K_{y}} \) , \( {K_{z}} \) represent spin correlation strengths [15]. This Hamiltonian has a dynamic frustration structure and can be exactly solved. The ground state of the solution is a gapped or gapless QSL state, known as Kitaev quantum liquid [15].

4.3. Examples of 2D Materials

With the advancement of neutron scattering techniques, an increasing number of 2D materials have been found to exhibit QSL phases.

YbMgGaO₄ is a 2D material, consisting of alternating layers of nonmagnetic YbMgGaO₄ and triangular lattice layers occupied by Yb³⁺ ions with an effective spin of 1/2 [16]. The magnetic interactions between Yb³⁺ ions mainly occur within the same layer, and the interlayer coupling is weak, making it a 2D material. In 2016, Paddison and his team conducted neutron scattering experiments on YbMgGaO₄, revealing a continuous magnetic excitation spectrum at very low temperatures that confirmed its QSL nature [17]. YbMgGaO₄ has antiferromagnetic exchange interactions in different directions, as well as anisotropic interactions due to strong spin-orbit coupling. The competition and cooperation between these interactions give rise to strong geometric frustration and quantum fluctuations, which ultimately stabilize the QSL state [17].

The α-RuCl₃ crystal structure comprises alternating nonmagnetic RuCl₆ layers and triangular lattice layers with Ru³⁺ ions having an effective spin of-1/2 [18]. Due to this structure, it is a 2D system. In 2017, Banerjee and colleagues conducted neutron scattering experiments on α-RuCl₃, which revealed the presence of scattering rods in a large energy range around the Brillouin zone center. This energy range remains stable with temperature variation, which is consistent with scattering from Majorana excitations in Kitaev QSLs. This indicates the QSL nature of the material [19]. Similarly, in α-RuCl_3, the competition and cooperation between interactions brings the material close to the Kitaev QSL state [18].

QSL goes beyond Landau phase transitions, providing insight into strongly correlated electron systems and cutting-edge fields like high-temperature superconductivity and quantum computing [20].

5. Conclusion

Two-dimensional quantum materials beyond carbon are currently a hot research topic in the field of materials science, owing to their exciting properties and potential applications. This article presents an overview of such 2D materials, exploring their unique properties and applications, such as superconductivity, ferromagnetism, antiferromagnetism, and QSL phases. The discussion on superconductivity covers both conventional superconductors, such as MgB₂, which follow the BCS theory, and unconventional superconductors, such as copper-based, iron-based, and Ising superconductors that go beyond it. These materials have the ability to eliminate electrical resistance entirely upon reaching their critical temperature, making them ideal for electronic devices and energy transmission applications. The article then moves on to ferromagnetism and antiferromagnetism, highlighting the incredible CrI₃. By manipulating parameters like the number of layers and strain in CrI₃, it’s possible to switch between ferromagnetic and antiferromagnetic states, which is crucial for the study of magnetic systems. Finally, the article concludes by discussing QSL phases, introducing the Kitaev model and citing two 2D materials, YbMgGaO₄ and α-RuCl₃, that exhibit QSL phases. These materials hold enormous potential for quantum computing and information storage. In summarize, 2D quantum materials beyond carbon possess remarkable properties and hold tremendous potential for various applications. Not only do these studies contribute to people’s understanding of materials science, but they also pave the way for technological advancements in electronics and quantum computing. As research and technology progress, physicists can anticipate uncovering even more unique properties and applications of these materials.