1. Introduction

The parameter tuning of PID controllers is an important step in the process of modern industry and accounts for over 95% of modern control [1]. More precise adjustment of controller parameters can enable the control system to output efficiently and stably. With the continuous development of the times and the development of industry, the complexity of controllers is increasing. Traditional PID parameter tuning methods cannot meet people's requirements, especially for complex systems with large time delays, time variations, and nonlinearity [2, 3].

Therefore, based on the traditional tuning process of PID, trial and error, logarithmic frequency response method, and critical proportion method, etc. are also included [4]. New algorithm models can be used to optimize traditional PID, such as genetic algorithms. Genetic algorithms simulate the law of survival of the fittest in natural populations on the basis of the principle of gene adaptation. The algorithm's basic principle is to encode, cross, mutate, and replicate the gene library of the basic parent group to generate a gene library of offspring. The gene libraries of the parent and offspring are then merged and the fitness of their genes is discussed. Ultimately, the genes suitable for survival are retained, and the solution to the problem is iteratively optimized. This process is similar to the tuning of PID control and is a continuous optimization process [5-7].

In addition to genetic algorithms, other optimization algorithms such as ant colony algorithm [8], ppaper swarm algorithm [9], deep learning, and other models can be used. This paper mainly discusses genetic algorithms, which have advantages such as clear logic, wide applicability, easy understanding of logic, and good iterative optimization effects [10]. It is also important to discuss and optimize the speed of iterative optimization using genetic algorithms, whose algorithmic drawbacks include uncertainty in the search capability, low speed of search and optimization, possible data bias or non-convergence of data born during data processing. The algorithm needs to be used with a certain level of data analysis. Therefore, it is worthwhile for the researcher to go into in-depth exploration and optimization in this area [11].

2. Methods

2.1. PID controller and genetic algorithm

2.1.1. Process and principles of PID controller parameter tuning based on genetic algorithm

The formula followed by traditional PID controllers is as follows:

\( u(t)=Kp×e(t)+Ki\int _{0}^{t}e(t)dt+Kd\frac{de(t)}{dt} \) (1)

1) Proportional link. The deviation signal e(t) is multiplied with the proportionality coefficient, when the deviation is generated, the proportional link will immediately produce the control effect to reduce the deviation;

2) Integral link. The integral of the deviation signal e(t) is multiplied with the integral coefficient, which is used to eliminate the static difference after the steady state and improve the accuracy of the system;

3) Differential link. The derivative of the deviation signal e(t) is multiplied by the differential coefficient to react to the trend of the deviation and can introduce the correction value in the system in advance before the error signal becomes too large, so as to speed up the control speed of the system and achieve the purpose of reducing the regulation time.

4) PID formula. Where U(t) is the actual output, e(t) is the actual error, Kp, Ki, Kd are the proportional, integral, and derivative gain parameters, which are also the parts that need to be tuned in the PID controller [12].

Furthermore, it can be deduced that the transfer function of a PID controller is

\( G(s)=Kp+\frac{Ki}{s}+KdS \) (2)

In Matlab, it can be represented as GSpid=pid(kp,ki,kd); In traditional PID controllers, the data obtained through conventional tuning methods often results in underdamped, slow response or large overshoot values, which means they do not meet our performance requirements. Therefore, the so-called optimization algorithm is used to optimize the numerical parameters of the PID controller through dynamic and adjustable search methods, making the iterative data results of the parameters converge. This is the process of optimization [13].

2.1.2. The optimization steps of genetic algorithm are as follows

1) Determine the mathematical model for the calculation. mathematically modeling the discussed problem.

2) Encode gene library. Set the size of the gene library population, the length of each gene, and determine the basic evolutionary parameters.

3) Edit population library. Perform operations such as mutation, replication, and crossover on the gene library.

4) Decode. Decode the genetic sequence to become the parameter values for iterative transformations in the model for discussion.

5) Calculate fitness value. Set the fitness conversion rules for genetic individuals and classify them as good or bad.

6)Gene selection. Eliminate gene sequences with low fitness values to improve the overall adaptability of the population [14].

Genetic algorithm does not directly process its direct data, but searches the coded clusters of its direct data, and is not constrained by the continuity of the function in the process of searching. Genetic algorithm uses an algorithmic model in which multiple points are searched together, which is highly synergistic and also allows for quick determination of the location of the optimized value. Many operation steps in the genetic algorithm such as crossover, mutation, etc. can be set to control the efficiency of cluster processing, and the weights can be changed according to different needs, wich resulting in the genetic algorithm's high flexibility and adjustable ability. The goal of the genetic algorithm is the result value of the function, in the process of operation, do not have to consider the impact of the function, in solving a variety of problems in a wider range, practicality is strong. The basic idea of the genetic algorithm is very simple, because based on the principle of heredity. So it is easier to understand, there is no fixed algorithm model to comply with. In the coding process can be more into their own understanding.

3. Simulation process and results

3.1. Selection of the objective function

In the process of optimizing the function, an objective function is needed to evaluate the merits of the parameter values. In the PID control model, there are several commonly used evaluation indicators, which are mainly discussed around the system error. In this paper, the sum of the absolute values of the system error integral is used as the performance evaluation indicator of the PID controller and also as the fitness of the experimental genome, namely the integral type of error absolute value. The formula is as follows:

\( J=\int _{0}^{t}|e(t)|w1dt \) (3)

The Matlab code implementation is: J=J+w1*abs(e)+w2*pos+w3*tr; % e is the system error w is the numerical parameter weight [15].

3.2. Model Selection

In the process of optimizing the function, it is necessary to discuss a certain mathematical model. This paper selects a DC motor as the ideal model for discussion, and its transfer function is:

\( G(s)=\frac{100}{{s^{2}}+30s+100} \) (4)

The Matlab code implementation is: G=tf(100, [1,30,100])

3.3. Establishment of Gene Library and Processing of Gene Library

First, the size of the gene pool is determined, the range of PID parameter values that need to be rectified is set, and the probabilities of the parameters underlying the genetic algorithm are set, such as the coding length, the probability of variation, and the probability of crossover. An i*j matrix is generated for storing the encoded gene pool as the parent population, where i represents the number of individuals in the population and j represents the length of the gene.

The example of the representation of genetic individuals in Matlab is: [1 8 5 3 6 0 6 3 6 1]. After the gene pool is generated, a new matrix is created for changes to the parent population.

Matrix X1 and X2 are responsible for the genetic crossover of the parent population: two random gene strands are selected, along with a random gene breakpoint, and the gene sequences before and after the breakpoint are exchanged.

Matlab code implementation is:

x1(i,:)=[gene(i,1:d),m(d+1:change*Long)];

x2(i,:)=[m(1:d),gene(i,d+1:change*Long)];

Matrix X3 is responsible for replicating genes in the parent population, copying gene sequences with higher fitness according to the probability of replication.

Matlab code implementation is:

If

rand<popterm; %popterm: probability of gene replication

d = randi(popnum); % popnum: the number of population

x(i,:) = gene(d,:);

End

Matrix X4 is responsible for mutating the genes of the parent population, that is, randomly selecting genes from the population according to the probability of mutation, and randomly assigning values to the genes after a random breakpoint.

Matlab code implementation is:

gene(i,randi(change*Long))=randi([0,9]);

x(i,:)=gene(i,:);

Finally, the transformed offspring population and the parent population is merged to generate a summary gene pool for individual optimization.

3.4 Optimize and iterate the gene library.

After obtaining the total population of the fused parent-child gene pool, the total population of the gene pool is decoded and the matrix is transformed to the specific values of Kp,Ki, and Kd.

The Matlab decoding process is:

for

i=1:Long

decode(i)=10^(Long-i);

end

result = gene * decode / (decode(1) - 1) / 10 * (b - a) + a;

% a and b are parameter ranges

After decoding, the three parameter values of Kp,Ki,and Kd are substituted into the objective function of fitness to obtain the fitness value of each gene, which is ranked, and the lower-ranked gene sequences are eliminated for processing. Finally the processed population is iteratively updated as a new generation of the parent population.

The Matlab control system is:

GSpid=tf([Kd,Kp,Ki],[1,0]);

Gs=feedback(GSpid*G,1,-1);

result=step(Gs,t)

4. Simulation results

4.1. Fitness Value Simulation Curve

From Figure 1 chart, it is clear that the fitness is decreasing after each iteration and then tends to converge, indicating that after genetic algorithm processing, the population is developing towards a more optimal direction in practice.

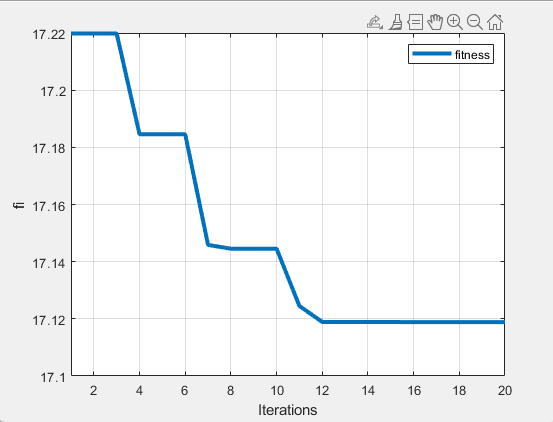
Figure 1. Fitness results (photo credited: original)

4.2. Simulation results of parameters Kp, Ki, and Kd

It can be seen that the parameters of the PID controller may appear random during the initial iterations, but after multiple iterations, they will tend to converge. The iterative transformations of Kp,Ki,Kd are shown in Figure. 2, Figure. 3, and Figure. 4, and the trends of these parameters are all initially dispersed and then eventually converge.

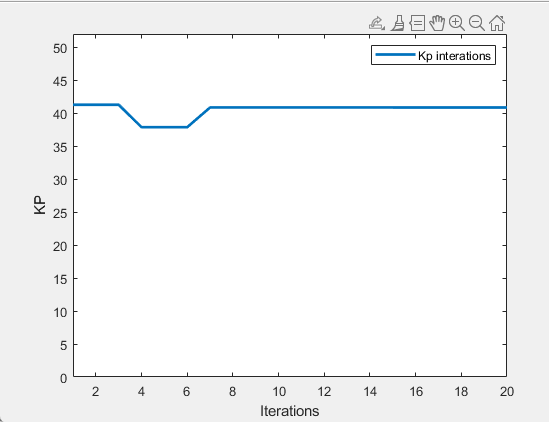
Figure 2. Kp results (photo credited: original)

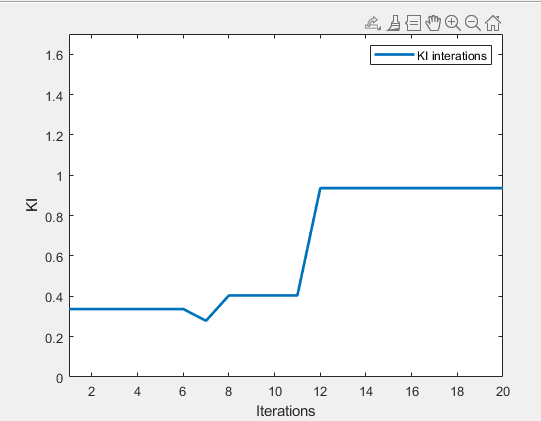
Figure 3. Ki results (photo credited: original)

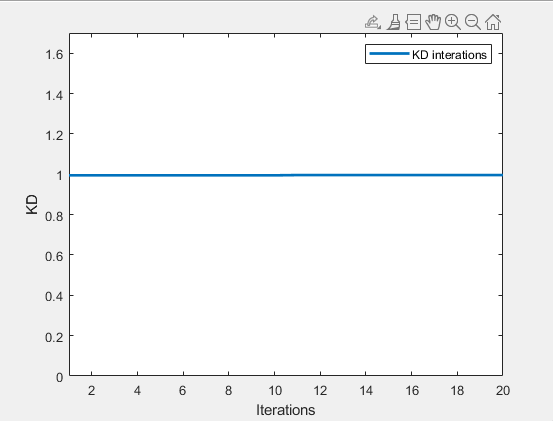
Figure 4. Kd results (photo credited: original)

4.3. Comparison of Simulation Results of PID Control Curves

This is the result graph presented by the self-tuning process with genetic algorithm, with Kp=40.8597, Ki=0.9361, and Kd=0.9959. Compared with the untuned PID control, the PID control adjusted by genetic algorithm is significantly closer to the desired output, with very small overshoot and static error. The system's adjustment time is also extremely small, greatly improving the stability and performance of the PID controller, and enhancing the efficiency of its use. The variation of the output of the step signal over time, the variation of the output of the tuned PID controller over time and the variation of the output of the untuned PID controller over time are shown in Figure. 5, and it can be clearly seen that the signal output of the tuned PID controller, which represented by the blue line, is more in line with the performance requirements.

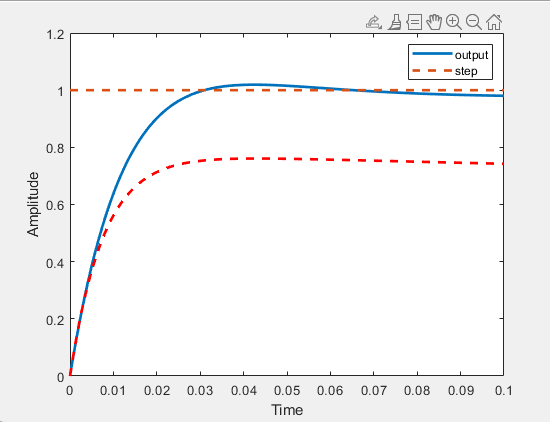
Figure 5. Output signal versus time (photo credited: original)

4.4. Problems encountered and prospects in the process of tuning PID parameters using genetic algorithms

In the process of simulation, if there are fewer iterations, it will cases where the parameter values do not converge, or n converging constants are obtained. The genetic algorithm in general can quickly determine the approximate range of the parameter values, and there will be cases in which the resultant parameters of more iterations have similar values to those of the resultant parameters of fewer iterations. Additionally, the efficiency of numerical optimization is higher in the early stages of iteration, while it significantly decreases and repeats in the middle and later stages of iteration. When obtaining the iterative result, it is also necessary to manually determine the availability of the iterative values. Therefore, this paper believes that the development direction of genetic algorithms can start from the second half of the iteration count, using faster algorithms to optimize the problem of efficiency decline in the second half of the genetic algorithm, and better determine the convergence value.

In the process of simulation, it is also important to design the number of iterations and the underlying parameters of the genetic algorithm skillfully. So many iterations may make the simulation process too long, in the preliminary simulation often choose 8-12 iterations. After the initial simulation, it is better to choose 20-50 iterations, more than 50 iterations of the value will find that the value has basically been determined, and can only rely on increasing the length of the gene to get a better value.

In the process of simulation, setting the parameter range of the PID controller is also very important, if the parameter is set too large, it may be found that the optimization model after iteration of the deviation of the situation, it is best to initially estimate the approximate value of the results, set a good range and then start the simulation.

In the simulation results, there may be occasional non-convergence of the situation, the probability that the reason is because the number of iterations is too small. Sometimes the optimized parameters do not change as the number of iterations increases. This may be related to the coding rules, or the optimal value may be found in the first iteration. The best way to deal with this is to check the total population coding changes in the iterations and re-do the simulation. Also try to change the objective function and the weights of the indices to see different simulation results. Change the different coding methods and the amount of size of the initial values to make the experiment generalizable.

5. Conclusion

As the most commonly used control model in the present era, the PID controller requires a significant amount of time and effort to adjust its parameter values during product manufacturing or model control processes. Not only does it require the adjuster to invest a certain amount of time cost to understand and learn, but it also cannot guarantee the superiority of the parameter values. The control results of manually adjusted PID controllers are often unsatisfactory, while the advantages of using the Ga algorithm for parameter adjustment proposed in this paper are obvious. This paper starts from the actual second-order motor system model, and introduces the practical steps, algorithm flow, selection of objective function, and Matlab implementation method for tuning PID parameters using genetic algorithms. From the simulation results, it can be seen that the parameter optimization process has better performance indicators, better curve forms, smaller overshoot, faster convergence speed, and better stability using the Ga algorithm optimized PID algorithm, which is also easier to understand. It is possible to optimize this algorithmic model in many other aspects, such as mutation, crossover, replication of the algorithm for speed improvement, handling of populations, etc. It is believed that this basic optimization model of the algorithm in the process of uninterrupted optimization and questioning will eventually bring great convenience to the modern computer as well as engineering fields.