1 Introduction

In recent years, with the development of science and technology and social progress, more and more artificial intelligence products have been applied to real life, from ordinary people to many large enterprises have begun to use artificial intelligence to assist life, which has also brought many problems, the most important of which is whether artificial intelligence can be used to predict upcoming hazards through some mathematical methods, such as natural disasters such as tsunamis, earthquakes and electromagnetic pulse noise. Therefore, Markov chains can be used to predict future events in mathematics and the derivation and application of some advanced formulas will be studied. and applications in other fields such as physics, meteorology, and engineering even medical to effectively reduce the damage to life and property caused by various disasters [1].

Markov chain has already been widely used in people’s lives. Because there are many factors affecting road construction costs, the use of Markov chain to predict can be very effective in filtering out some factors with less influence. It can also get relatively more accurate data very quickly. In addition to road construction, Markov chains can also be applied to market share analysis and forecasting in finance. Wu found that that the transfer matrix calculation of Markov chain can be well applied to predict market share [2]. In addition to architecture and finance, Markov chains can also be used to predict power impulse noise. It is found that Markov chains can effectively calculate the probability of excessive power pulses, and Markov chains can be well used by artificial intelligence, so they are very effective in preventing excessive noise [3].

In this essay, the author will examine the principles of Markov chains used to predict future events, as well as the derivation and application of advanced formulas for Markov chains. In the third part, we will deal with some of the real-life ways in which Markov chains can be used to predict future events, including in the fields of physical meteorology and engineering.

2 Methods and theory

2.1 Markov chain

The basic idea of the Markov chain is that the probability of the next event occurring is only related to the state of the current event, which means that the event will not be affected by how current situation comes. For example, the famous gambler’s bankruptcy model can be solved by using the Markov chain. The question stem is as follows. If a gambler uses a coin toss to gamble money, let his stake be $N$ for every win and lose for every dollar, and stop when he loses all or wins M dollars, and the probability of winning or losing is $1/2$ [4]. This paper will address two questions. One is the probability of losing all the money on condition that the principal is 0 or $M$ , while the other is the way to write a general term expressing $P(N)$ .

First of all, for the first question, when $N$ is 0, one has $P(N)=P(0)= 1$ . This is because the principal is zero and it is already over without losing money, so the same is true when $N$ is M, i.e.,

$P(N)=P(M)=0.\ \ \ (1)$

About the second question, set two events A and B, event A is that N yuan is all lost, and event B is N yuan to win the next game. For these two events you can get the formula $P(A)=P(BA)+P(\overline{B}A)$ , so

$P(A)=P(B)P(A|B)+P(\bar{B})P(A|\bar{B}).\ \ \ (2)$

The Eq. (2) can be obtained according to the full probability formula and previous formula, and it can be simplified as $P(A)=\frac{1}{2}P(n-1)×\frac{1}{2}P(n+1)$ . So, it can be sure that when the probability of win and lose one time are same the $P(A)$ is arithmetic progression which have common difference, Let $d$ can be found by $P(N)-P(N-1)=d$ , $P(N-1)-P(N-2)=d$ , and so on until $P(1)-P(0)=d$ . If add all these up, $P(N)-P(0)=Nd$ , then the finally relation

$P(N)=1-\frac{N}{M}.\ \ \ (3)$

can be gotten, which is the probability of bankruptcy when the principal amount is $N$ dollars and the expected value is $M$ .

Another basic way to use this chain is the random walk. The one-dimensional random walk is easy to show. The stem is that for a person walk in a number line, he can walk right or left and the probability of this two is $1/2$ . The question is in two steps what is the probability he can come back to the original point. Apparently, the matrix can be made as [5]

$R=[\begin{matrix}0 & -2 & -1 & 0 & 1 & 2 \\ -2 & 0 & 0.5 & 0 & 0 & 0 \\ -1 & 0.5 & 0 & 0.5 & 0 & 0 \\ 0 & 0 & 0.5 & 0 & 0.5 & 0 \\ 1 & 0 & 0 & 0.5 & 0 & 0.5 \\ 2 & 0 & 0 & 0 & 0.5 & 0 \\ \end{matrix}].\ \ \ (4)$

The first row means the start point while the first column means the finish point. After one step the number in the matrix except first row and column means the probability get to the new point. This is because that the man goes two steps so this matrix needs to be squired because the need is only from 0 point to 0 point so just need to count out fourth row and column and can get number 0.5 which means after two steps the probability get to the original point is half.

These are two basic ways to use Markov chain in mathematics. According to Chapman-Kolmogorov equation [6], $r_{ij}(n)=\sum_{k=1}^{m} r_{ik}(n-1)p_{kj}$ . Here, $r_{ij}(n)$ indicates the probability of reaching state $i$ after $n$ steps from state $j$ . It can be found that the greater the number of steps n, the smaller the dependence on the initial state which is state $i$ .

2.2 Recurrent and transient

In addition to the above two applications, Markov chains can be applied in mathematics to other places, such as distinguishing between different states of events, some states that can be accessed multiple times but others that can only be accessed a limited number of times. When $r_{ij}(n)≥0$ means that it is possible that state j can be reached after n steps from state $i$ . It is divided into two types based on whether they can return to their original state or not. The first is the recurrent. That is, all the reachable states of state $i$ can return to state $i$ . The second is the transient. That is, there is state $k$ , which can be reached by state $i$ but cannot be return to state $i$ [7].

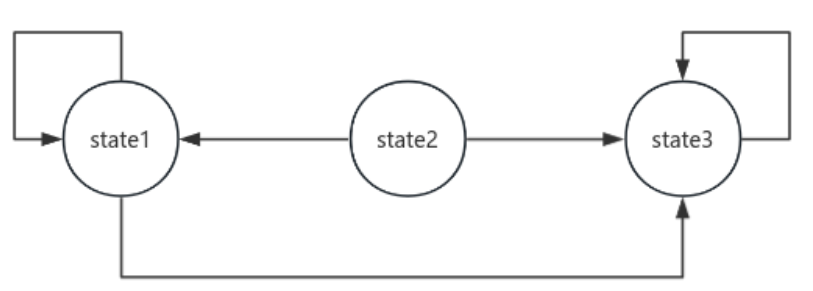
Figure 1. An example of simple Markov chain

For example, in the Figure 1, the state 1 and state 3 are both recurrent, while the state 2 is transient because state 2 cannot go back to itself after transitioning to state 1 and state 3. Besides, Markov chains are also cyclical. When a recurrent class can be divided into $d \gt 1$ adjacent subsets, $S_{1},S_{2},⋯,S_{d}$ , and satisfied $i∈S_{k}$ and $p_{ij} \gt 0$ , $j∈S_{k+1}$ ( $k=1 …… d-1$ ), and $j∈S_{1}$ ( $k=d$ ), these two equations can be gotten. This means that this recurrent class is cyclical.

2.3 Other examples

When there is only one recurrent class, and this recurrent class is not cyclical, this kind of Markov chain has characteristics $\lim{n→∞}{r_{ij}(n)=π_{j} ,} ∀i, j∈R$ . The steady-state probability $π_{j}$ is the only solution to the following two equations $π_{j}=\sum_{k=1}^{m} π_{k}P_{kj}$ and $1=\sum_{k=1}^{m} π_{k}$ . Another typical characteristic is that when $π_{j}=0$ for all transient state $j$ and when $π_{j} \gt 0$ is for all recurrent state $j$ . For example, if there are two states in the Markov chain and the transfer probability is that $P_{11}=0.6, P_{22}=0.7, P_{12}=0.4, P_{21}=0.3$ . According to the balance equation, $π_{1} = π_{1}P _{11}+π_{2}P_{21}$ , $π_{2}=π_{1}P _{12}+π_{2}P_{22}$ , and $π_{2} + π_{1}=1$ . The later can get $π_{2}=\frac{4}{7}$ and $π_{1}=\frac{3}{7}$ [8].

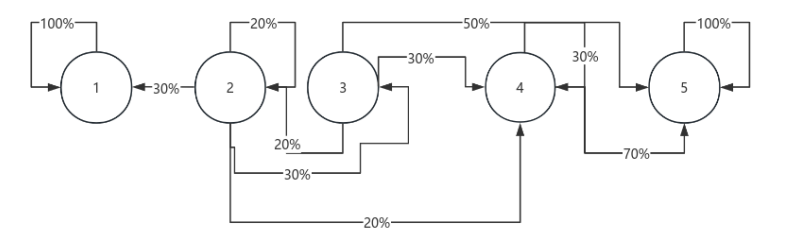
Figure 2. A complex figure of how states change to each other.

Another example is that a young man has two cars which are going to be used to go work or back home if it rains on the road and it rains in his location, he will drive, if it does not rain, he will walk, and if the probability of each rain is $P$ . The question is that what is the steady-state probability that the person will get wet on a given day? In this event that he has $i = 0,1,2$ cars in his location, the transfer probability matrix is $[\begin{matrix}0 & 0 & 1 \\ 0 & 1-p & p \\ 1-p & p & 0 \\ \end{matrix}]$ . Next, image that there is only one recurrent class in the Markov chain which is not cyclical, then the balance equation is $π_{0} = (1-p)π_{2}$ , $π_{1} = (1-p)π_{1}$ + $pπ_{2}$ , and $π_{2} = π_{0}$ + $Pπ_{1}$ . A way to solve the complex question of Markov chain is to take two states in to a big state and to solve. From the Figure 2, the question to ask is the probability from each state reach the recurrent class ${4,5}$ , over here can combine ${4,5}$ to state 6. $a_{1}=0, a_{2}=0.3a_{1}+0.2a_{2}+0.3a_{3}+0.2a_{6}, a_{3}= 0.2a_{2}+0.8a_{6}, a_{6}=1$ . In this way, one can easier to find out the answer instead of making longer formula, in conclusion $a_{1}$ =0, $a_{2}=\frac{22}{37}, a_{3}=\frac{34}{37}, a_{6}=1$ .

3 Results and Applications

In addition to mathematics, Markov chains can also be used in many other applied disciplines, such as the prediction and analysis of e-commerce market share in finance, the construction and calculation of bridge degradation probability models in architecture, and the prediction of the amount of noise emitted by electromagnetic pulses in the surrounding facilities in physics.

When people want to predict the damage of impulse noise, the impulse noise will be there. Some time it is as weak as background noise but some time it is very powerful, and the relation between them is very random. Thereby, the Markov chain can be used to predict the probability of the damage noise occur. First, choose the noise rapidly, and order them from smallest to the biggest, and stipulate the biggest as $U_{m}$ . So, if there are 10 rapids one can write them as $[U_{i}, \frac{U_{i+1}}{10})$ ( $i = 0, 1, 2, ⋯, 9$ ). This can be used to classify the state of noise, and according these 10 states, one can make a matrix with size $10×10$ like the bigger one of the first image of this paper the number in side it is the probability from last state to the current state. The symbols $P_{ij}$ means that the probability form state $i$ to state $j$ . Let $P_{23}$ means that the probability from state 2 to state 3, and if one wants to find out the probability in $n$ steps, it needs to power this matrix with $n$ times. Moreover, to avoid the damage form, the big noise just needs to print out the last few columns, and the probability decides whether people need to prepare to act.

Markov chain can also help people to predict the weather. For example, if the first day is sunny and there are some data of the probability that weather transfer each other. The sunny to rainy is 0.4, sunny to foggy is 0.3, sunny to sunny is 0.3, foggy to rainy is 0.5, foggy to sunny is 0.2, foggy to foggy is 0.3, rainy to foggy is 0.6, rainy to sunny is 0.2, rainy to rainy is 0.2. By these known data, a matrix can be made. By using this matrix people can predict what the weather it is in many days later. If today is sunny in 2 days later, the probability of sunny weather is 0.23 rainy is 0.35 foggy is 0.3 [9].

Markov chains can also be applied to the fragility analysis of a ship. If the ship $A$ has 12 compartments, wherein there is system $A$ , and the connecting line passes through cabins 1, 2, 3, 5, 8, 11, wherein in cabins 1, 3, 11 there are equipment $e_{1},e_{2},e_{3}$ respectively. The $B$ system passes through compartments 7, 8 and 9, where in compartments 7 and 9 there are equipment $e_{4}, e_{5}$ . It is assumed that the system $AB$ is independent of each other, and they can operate separately without affecting each other. A compartment will be destroyed at a fixed interval of time, and the same compartment can be destroyed many times, and the probability of each compartment being damaged is the same, and it will not be repaired after being destroyed. For this case there can be state $S_{1},S_{2},S_{3},S_{4}$ , which are that the $AB$ system is normal, only the $A$ system is normal, only the B system is normal, and the $AB$ system is not normal. The transfer matrix $T$ can be derived from the calculation, and the relation is shown in Figure 3.

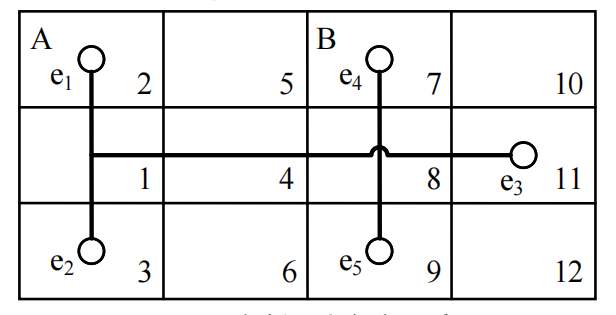
Figure 3. The image inside the ship [5].

Likewise, the matrix can be made as

$R=[\begin{matrix}4/12 & 2/12 & 5/12 & 1/12 \\ 0 & 6/12 & 0 & 6/12 \\ 0 & 0 & 9/12 & 3/12 \\ 0 & 0 & 0 & 1 \\ \end{matrix}].\ \ \ （5）$

The columns of this matrix represent the starting point, and the rows represent the arrival point, i.e., $T_{12}$ is the probability transform from state 1 to state 2, which means it transform from no system corruption to only system B corruption. Using a vector $S(h) = s(0)T^{h}$ , in this equation h is the number of breaks. $S(0)$ is the initial state $S(0)=[1 0 0 0]$ .

When it is necessary to calculate a higher power, it can be obtained by diagonalization [10]

$S(h)=s(0)T^{h}=S(0)P^{-1}D^{h}P.\ \ \ (6)$

In this equation, $D$ is the diagonal matrix, $P$ contains its respective eigenvectors, $T$ is always a triangular matrix because the repair of the system is not considered, and the eigenvalues of $T$ are the elements on its diagonal. Therefore, the diagonal of $D$ and the diagonal of $T$ contain the same value. It is found that $P_{r}(s_{1}) = λ_{1}^{h} = (4/12)^{h}$ , $P_{r}(s_{2}) = -λ_{1}^{h}+λ_{2}^{h} = -(4/12)^{h}+ (9/12)^{h}$ , $P_{r}(s_{3}) = -λ_{1}^{h}+λ_{3}^{h} = -(4/12)^{h} + (9/12)^{h}$ , and $P_{r}(s_{4}) = λ_{1}^{h}-λ_{2}^{h}-λ_{3}^{h}+λ_{4}^{h} =(4/12)^{h} -(6/12)^{h}- (9/12)^{h}+1$ . Here, $λ_{1},λ_{2},λ_{3},λ_{4}$ are all eigenvalues of $T$ .

4 Conclusion

This paper introduced some principles of Markov chain in mathematics and the derivation and practical applications of several formulas. These include the meaning and characteristics of transients and cycles, and the cases in which two different states can be reduced to one state in some cases of Markov chain. After that, it also introduces how Markov chain can be used in applied physics. This is because that the Markov chain is a very important way to analyze random probabilities between different states and it is specialized in the probability transfer of different states. In this case they can be used to help workers prevent excessive electromagnetic pulse noise faster and more accurately, in meteorology they can easily predict the weather conditions in the next few days by the probabilities corresponding to the conversion of states to each other. In addition, it also plays a role in engineering the probability transfer matrix, which is used to calculate the probability of damage to each component. In doing so, it can let people know when they should repair the ship. To conclude, this paper underscores the importance of the Markov chain in divergent fields of science.