1. Introduction

The phenomenon of Random walk means that an event is only based on the past performance, and the future route of a spot in different dimensions cannot be determined. It is also the ideal mathematics state of Brownian motion. It means that in each space, a spot can move to every direction in one step with the same possibility and each step is independent and random. For example, in each two-dimension plane, a spot whose size is negligible, starts from the origin and in a same interval, it has four choices of directions to move on: left, right, forward, and backward with the same possibility. In the next interval, the spot will face the same choice again with each interval completely independent. Thus, every step is at random and the route is unpredictable [1].

This is a very common phenomenon in many fields, widely ranging from physics, finance (e.g., predicting the stock market), biology computer science and statistic. The theory of random walk has been discussed for many years. Some decades ago, the Brownian motion was first combined with stock to describe the price of stocks in the famous work Theory of Speculation by Louis Bachelier. Then in 1923, N. Wiener gave the mathematics definition of Brownian motion, so that the mathematics Brownian motion is also called Wiener Process by later scholars. In 1931, A. N. Kolmogorov laid the groundwork for Markov chain. Obviously, random walk is of great significance for humans [2].

In this paper, the authors are going to analyze specific use of random walk in Finance, Physics and Biology. Three topics will be mainly focused on in the paper, which are Wiener Process, Brownian motion, and Pu migration. To reach the target, the author will select several references of typical random walk application to analyze how people apply random walk into different fields. Although applications of random walk are very mature, there is still spare space to research, trying to figure out traditional ways of using it and explore possible innovation. After the introduction, the application of random walk in Wiener Process, Brownian motion and Pu migration will be talked about in this order.

2. Brownian motion

2.1. Definition and Theory

Brownian motion is the most fundamental class of stochastic processes. A stochastic process \( W(t) \) \( (t \gt 0) \) is defined as a Brownian motion when the increments of \( Δt \) for each time period of the stochastic process \( W(t) (t \gt 0) \) are independent of each other and follow a normal distribution \( N(0,Δt) \) (independent and normal increments) [3]. This process was first discovered by British botanist Robert Brown, when he found that pollen floated in water shook heavily under the microscope. Water molecules are doing irregular movements and they keep hitting the pollen. Thus, the pollen sloshes heavily and doing random movements too.

Random walk means in each space, a spot can move to every direction in one step with the same possibility and each step is independent and random. Besides, the whole process is constant. The core concept is that the conserved quantities carried by any irregular walker each correspond to a diffusive transport law. Close to Brownian motion, the ideal mathematical state of Brownian motion, which at this stage is mainly used in Internet link analysis and financial stock markets. The typical trajectory of a Brownian particle is shown in Figure 1 [4].

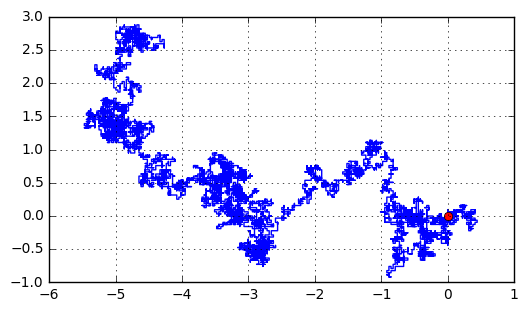
Figure 1. Illustration of the Brownian motion [4].

2.2. Similarities and differences

Brownian motion can be considered as a special model of random walk. The route of the molecule cannot be determined but people can use stochastic differential equation to describe it. Both of two motions can describe the random process, but Brownian motion is more proper to set up the model of constant question. Mathematically, the Stirling’s approximation formula, \( n!≈\sqrt[]{2}πn{(\frac{n}{e})^{n}} \) , is used to calculate the possibility in random walk [5].

For concentration, the authors shall calculate the possibility of a spot in dimension 2 doing random walk and returning in \( 2n \) steps ( \( n \) is an integer). Let \( {h_{1}},{h_{2}},{h_{3}},{h_{4}} \) represent the steps of moving left, right, up and down. As the spot finally return to the origin, \( {h_{1}}={h_{2}},{h_{3}}={h_{4}} \) . Let \( 2n={h_{1}}+{h_{2}}+{h_{3}}+{h_{4}} \) and \( k={h_{1}}={h_{2}} \) , so, \( {h_{3}}={h_{4}}=n-k \) [6]. The possibility can be expressed like \( \sum _{n=0}^{∞}(\frac{2n}{2k})(\frac{2k}{k})(\frac{2n-2k}{n-k}){\frac{1}{4}^{2}} \) . Using the Stirling’s approximation formula, one can get the result is \( \frac{1}{πn} \) .

3. Wiener process

3.1. Definition and Theory

A process is a Wiener process if it is a Markov process and the expected value of the variable change per unit time obeys a normal distribution with an expectation of 0 and a variance of 1. As can be seen from the definition, the Wiener process adds a qualifier to the Markov process. This process is used in physics to describe Brownian motion, so the Wiener process is also known as Brownian motion. The mathematical expression can be treated as \( ∆z=ε\sqrt[]{∆}t \) and \( ε~Φ(0, 1) \) [7].

The Wiener process is a stochastic process named after the French mathematician Wiener. It is used in numerous fields, such as physics, engineering, and probability theory, among others. With the rapid development of modern financial markets, the Wiener process has become one of the effective tools for financiers to study and predict stock prices, market fluctuations and other issues. In this article, the authors will explore the application of the Wiener process in finance and discuss possible future trends. The Wiener process is a stochastic process with a mean of zero in an infinitesimal time interval, a finite variance, and strong randomness. It is essentially a random walk, characterized by a random number at each point in time, over several time intervals. In finance, the Wiener process is a special kind of Brownian motion, which is an irregular free movement that changes in an irregular manner. Brownian motion can be thought of as a small ball floating in the air, and its small vibrations caused by collisions or disturbances cause irregular displacement that stays in a certain area. In financial markets, stock prices are also characterized by a Wiener process, which changes irregularly over several time intervals. Therefore, the Wiener process is one of the basic concepts in finance to study the movement of stock prices. The Wiener process has a wide range of applications in finance, including stock price forecasting, option pricing, and risk management.

3.2. Applications

The Wiener process simulates the movement of a stock’s price. In the financial markets, investors’ predictions about stock prices have always been a hot topic. The Wiener process can help investors make predictions about the price of a stock, thereby increasing the success rate of the investment. Through the statistics and analysis of various indicators such as the fluctuation frequency and variance of stock prices, the corresponding strategy can be formulated. Investors can use the Wiener process for stock selection and buying and selling strategy. In addition, it is also helpful for option pricing. An option is a financial derivative whose price is closely related to the price of a stock. The Wiener process can be used to simulate and analyze option pricing. When it comes to option pricing, the Wiener process is able to provide more accurate price predictions than Brownian motion, and can predict the volatility of option prices through extended models [8].

The Wiener process also plays an important role in risk management. By analyzing various probability, volatility, expected return and other issues in risk management, a more scientific and reasonable risk management strategy can be formulated. The application of the Wiener process allows investors in the market to assess risk and return more accurately and to have a better grasp of their investment decisions.

With the changes and innovations in financial markets, the application of the Wiener process in finance will also continue to expand. In the future, the application will be more extensive, including stock trading, financial derivatives pricing, risk management and other aspects. At the same time, the models and algorithms based on the Wiener process will continue to improve, making the application of the Wiener process in finance more accurate and effective. Especially with the continuous development of artificial intelligence technology, algorithms based on the Wiener process will be widely used in the field of intelligent investment to achieve more intelligent and automated investment transactions. In conclusion, the Wiener process is a widely free and very important stochastic process in the field of finance. With the development of financial markets and the continuous improvement of technology, the application of Wiener process in finance will be more extensive and accurate [9].

4. Pu migration

Continuous-time random walk is a mathematical model used to describe the process of stochastic movement in continuous time. In this model, an object or a particle will move in one, two, or higher-dimensional space with random step lengths and random directions. This part will introduce the Continuous-time random walk in Pu migration [10].

Pu (Plutonium) is one of the focus elements in research on high-level waste disposal, which belongs to the actinide series elements with an atomic number of 94. The atomic mass of its isotopes ranges from 232 to 246. The isotopes of primary concern are 238Pu, 239Pu, and 242Pu, with half-lives of 87.8 years, 2.41 × 10⁴ years, and 3.73 × 10⁵ years, respectively. The colloidal forms of Pu in the groundwater mainly contains true colloids and pseudo-colloids. For true colloids, they are mostly generated through hydrolysis or complexation reactions of Pu (IV), exhibiting diffusion and kinetic adsorption effects related to their stability, which can cause a noticeable tailing effect in breakthrough curves. Pseudo-colloids stand for Pu rapidly adsorbing onto various natural colloids in groundwater, it may have a fast adsorption process, and the Pu adsorbed onto colloids has a lower desorption kinetic constant, enhancing Pu’s migration capacity on mobile colloids. Traditional solute transport models consider Pu as a slow-migrating, poorly soluble, strongly adsorptive element.

One can use Continuous-Time Random Walk (CTRW) to describe the migration behavior of Pu in fractured rock column experiments, and it fits the measured breakthrough curves, identify corresponding model parameters, compare the fitting effects of different models, and then select the optimal model to simulate Pu migration behavior in fractured media under different colloid concentrations, analyzing the impact of colloids on Pu migration behavior and corresponding parameter variations.

To begin with, CTRW is a generalization of physical diffusion processes which can describe anomalous diffusion efficiently, including the super-diffusive or sub-diffusive cases. An equivalent formulation of the CTRW is given by generalized master equations. A connection between CTRWs and diffusion equations with fractional time derivatives has been established. Similarly, time-space fractional diffusion equations can be considered as CTRWs with continuously distributed jumps or continuum approximations of CTRWs on the lattices. In mathematics, a CTRW is a generalization of a random walk where the wandering particle waits for a random time between each jump. Therefore, it is a stochastic jump process with arbitrary distributions of jump lengths and waiting times. More generally it can be seen to be a special case of a Markov renewal process.

Here is a basic formulation: \( X（t）={X_{0}}+\sum _{i=1}^{N(t)}∆{X_{i}} \) and \( P(X,t)=\sum _{n=0}^{∞}P(n,t){P_{n}}(X) \) . Therefore, people can calculate the probability for the process taking the value X after n jumps, and \( P(n,t) \) is the probability of having n jumps after time t according to this basic formula. In this experiment, Anomalous Diffusion Equation (ADE) and CTRW can be used. ADE is a partial differential equation used to describe the movement of particles in non-standard diffusion processes, where the diffusion coefficient may be a function of time and/or space. This model is typically applicable to describe diffusion processes with spatial memory effects, such as confined diffusion or diffusion in heterogeneous media. According to the information provided, experimental data indicates that the migration behavior of Pu (Plutonium) exhibits pronounced non-Fickian characteristics, and the Breakthrough Curve (BTC) shows early arrival and tailing effects [11]. The early arrival phenomenon is mainly attributed to the presence of dominant fractures in the medium, which provides preferential pathways for Pu colloid migration, while the tailing effect is related to the diffusion and settling processes can be considered as the stability of Pu colloids.

It can also be known that results of the BTC by the ADE model are not satisfactory which may produce some problems because the early arrival and tailing phenomena of BTC are difficult to characterize well. This is caused by the parameters of the traditional ADE model have scale effects and cannot adequately describe the complex adsorption-desorption and colloid migration mechanisms. Therefore, compared with this, in contrast, the fitting results by the Continuous Time Random Walk-Two-Particle Langmuir (CTRW-TPL) model are superior, with higher coefficients of determination and lower root mean square errors, enabling better fitting of asymmetric BTCs. Additionally, the TPL model can describe the transition time from Fickian to non-Fickian migration through the parameter β. As the result, based on the provided information, it can be concluded that the CTRW-TPL model is more suitable than the ADE model for describing the migration behavior of Pu in the medium. It can provide more accurate fitting results and better describe the non-Fickian migration as well as the early arrival and tailing effects during the migration process. The Pu breakthrough curves fitting using three CTRW models are shown in Figure 2. The experimental observation is also presented for comparison.

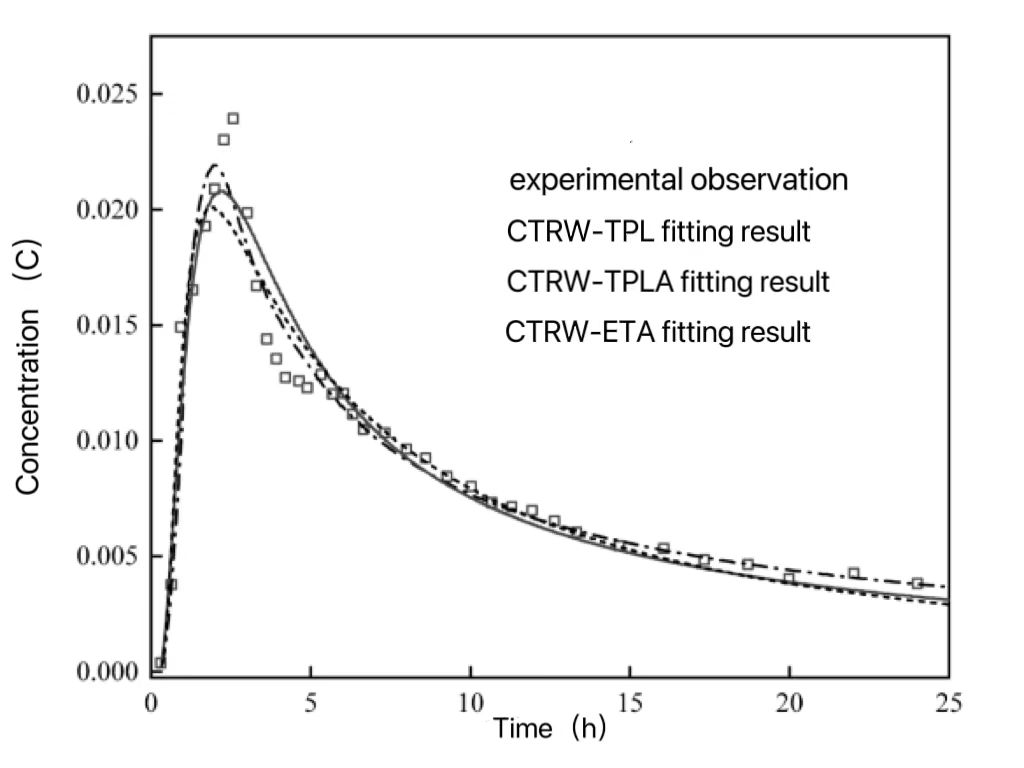
Figure 2. Pu breakthrough curves fitting using three CTRW models [10].

5. Conclusion

This paper explores the concept of stochastic processes from three specific models. Brownian motion has continuity and smoothness, people can use stochastic differential equation to describe it, and it is widely used in physics, finance, and other fields. It is more suitable for modeling and analyzing of continuity problems, especially for setting up the model of constant question. Wiener process is a continuous time stochastic process and considered to be a special kind of Brownian motion in finance, it can describe random phenomena and solve a deal of complex problems, such as in stock price prediction, risk management, future trends and so on. Pu transfer is a high-quality solution to solve random walks by using continuous time random walk to describe the migration behavior of Pu in fractured rock column experiments, and the concrete model and solution of stochastic process are not only these, it is found that stochastic process is an esoteric model, and one can further explore other models and applications related to follower processes in the future.

Authors Contribution

All the authors contributed equally and their names were listed in alphabetical order.