1. Introduction

Real life is often characterized by a lack of order, stability, and certainty. Instead, it exists in a constant state of randomness, disorder, and imbalance. Put simply, it’s impossible to precisely predict what will occur in the future, often referred to as fate. Does a nonlinear system have specific rules to follow? Nonlinear systems are inherently chaotic and unpredictable, so it’s natural to question the existence of any set rules to govern them. Nonlinear systems are governed by laws, yet their long-term state remains unpredictable. An example of a nonlinear system is the simple pendulum, which can be analyzed using principles from physics. This linear system is quite straightforward, and its outcome can be precisely determined once it reaches the desired position. However, when a line is introduced or a ball is affixed underneath, it transforms into a double pendulum [1]. This double pendulum is certainly predictable, but it’s impossible to accurately predict its next swing position due to its nonlinear nature. It has the potential to cause disorder. Chaos is the term used to describe the occurrence of random and irregular motions within a specific system. These chaotic phenomena cannot be predicted or repeated, but they can be mathematically or physically described [2]. For instance, in the case of the double pendulum depicted above, its motion can be described using physical equations. However, with each movement, it generates an apparently unpredictable curve, revealing the inherent chaotic nature of the system. Studying the relationship between chaos science and fractals can provide valuable insights into the understanding of chaotic phenomena in nonlinear dynamical systems and the intricate patterns they form [3].

This study seeks to provide an introduction to the fundamental concepts and characteristics of chaos and fractals, and explore their significance in the realm of mathematics and practical applications. By utilizing literature review and theoretical analysis, this paper aims to deepen readers’ understanding of the connection between chaos and fractals. Additionally, it offers a fresh approach for individuals to navigate complex systems and data.

2. Definition and relationship of chaos and fractals

The 1D logistic chaotic map is \( {x_{n+1}}=r{x_{n}}(1-{x_{n}}) \) [4]. In a simple way, this formula represents the relationship between the quantity of certain things. If the quantity of a kind of species decreases below a certain level in one year, the quantity of this species will increase in the next year. However, if the quantity of a certain species increases too much, the competition for living space and resources will cause the quantity of this species to decrease, where R is an adjustable parameter. When R is less than 3.5, the number of species changes regularly. However, when R>3.5, the number of species will suddenly become unpredictable. There are various possibilities, making it completely unpredictable.This is the characteristic of chaos [5].

The image below reflects the characteristics of a fractal. That is, when zoomed in, the local picture looks similar to the whole, exhibiting self-similarity.

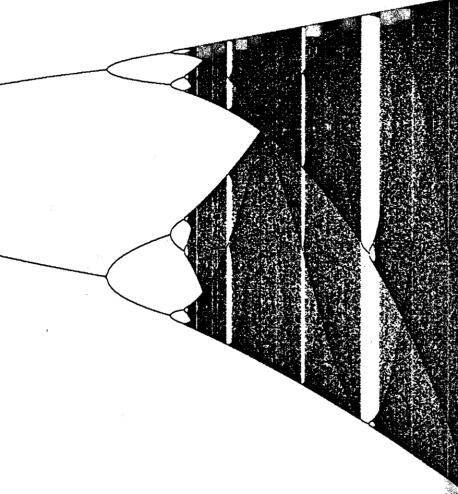
Figure 1. The representation of characteristic of chaos [6]

To illustrate the relationship between chaos and fractals, the example of a fractal repeller is considered. More concretely, the mapping of the line given by

\( T(x)=\begin{cases}sx if x≤a \\ \frac{a}{a-1}s(1-x) if x \gt a\end{cases} \) (1)

is also considered, where the parameters satisfy \( a∈(0,1); sa \gt 1. \) Its graph looks like figure 2.

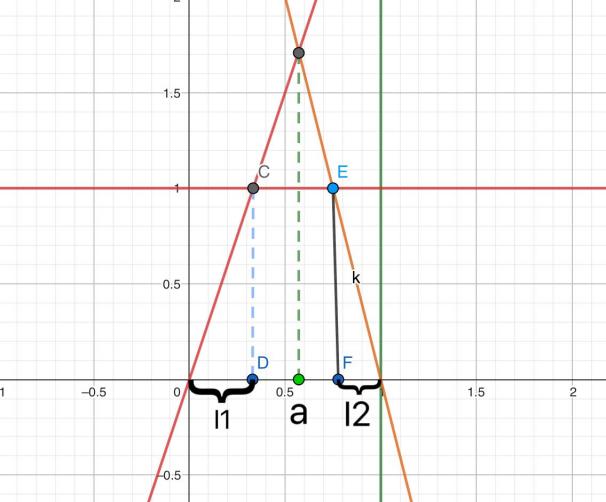
Figure 2. The relationship between chaos and fractals

First, if x is not in [0,1], then its orbit goes to minus infinity, which is represented as below:

\( x∉{I_{1}}∪{I_{2}}{T^{n}}(x)∉[0,1] ∀n∈N \)

Within the interval [0,1], three sub-intervals are identified, the first and last of which map onto the whole interval [0,1], and the middle one maps out of [0,1] in one iterate of T.

\( x∈{I_{1}}∪{I_{2}}T(X)∈[0,1] \)

This paper is interested to describe the set P of points x in [0,1] whose forward orbit remains within [0,1] for all iterates of T. Note that the points in [0,1] that remain in [0,1] under one iterate of T form the sub-intervals \( {I_{1}} \) and \( {I_{2}} \) . These sub-intervals can be obtained as images of [0,1] under \( {f_{1}} \) and \( {f_{2}} \) that are the inverses of the maps \( {T_{1}} \) and \( {T_{2}} \) . Note that \( {f_{1}} \) and \( {f_{2}} \) are contractions in the sense that they shrink the distance between any pair of points uniformly.

Now the points in [0,1] that remain in [0,1] under two iterates of T is considered. It is worth notable that points in \( { I_{1}} \) that are mapped to \( {I_{1}} \) by T are the points in \( {{I_{11}}≔f_{1}}({I_{1}}) \) ; points in \( { I_{1}} \) that are mapped to \( {I_{2}} \) by T are the points in \( {{I_{12}}≔f_{1}}({I_{2}}) \) ; points in \( { I_{2}} \) that are mapped to \( {I_{1}} \) by T are the points in \( {{I_{21}}≔f_{2}}({I_{1}}) \) ; and points in \( { I_{2}} \) that are mapped to \( {I_{2}} \) by T are the points in \( {{I_{22}}≔f_{2}}({I_{2}}) \) .

By continuing calculating this argument \( n \) times, it can be obtained that \( {2^{n}} \) sub-intervals \( {I_{{s_{0}}....{s_{n-1}}}}{f_{{s_{0}}}}∘⋯∘{f_{{s_{n-1}}}} \) ([0,1]) consisting of points in \( {I_{{s_{0}}}} \) that maps into \( {I_{{s_{1}}}} \) under one iterate of T, and into \( {I_{{s_{2}}}} \) under two iterates of T etc. Let \( {P_{n}} \) . The sets \( {P_{n}} \) are nested \( {P_{n}}⊆{P_{n-1}} \) because \( {I_{{s_{0}}⋯{s_{n-1}}}} \) ⊆ \( {I_{{s_{0}}⋯{s_{n-2}}}} \) and \( {P_{n}} \) =F( \( {P_{n-1}}) \) . Moreover, their intersection consists of points that never escape the interval [0,1] x \( ∈ \) P \( ∀n,x∈{P_{n}} \) ,i.e, \( {T^{n}}(x)∈[0,1] \) . In other words, P \( \bigcap _{n=1}^{∞}{P_{n}} \) .

To study the fractal properties of \( P \) , the Iterated Function System (IFS) is introduced on the space of fractals \( H([0,1]) \) consisting of all nonempty closed subsets of the interval \( [0,1]. \) Define

\( F:H([0,1])→H([0,1]), F(A)≔{f_{1}}(A)∪{f_{2}}(A). \)

Note \( F([0,1])={I_{1}}∪{I_{2}}={f_{1}}([0,1])∪{f_{2}}([0,1]) \) and \( {F^{n}}([0,1])={P_{n}}. \) Since \( {f_{1}} \) and \( {f_{2}} \) are contractions, so is F, and hence, by the Contraction Mapping Theorem, F has a unique fixed point in \( H([0,1]) \) . This fixed point is noted as \( P \) .

To see this hypothesis, F(P)=P is verified. By properties of the sets \( {P_{n}} \) , it can be obtained that F(P)=F \( \) = \( \) = \( \) = \( \) =P, which proves the claim.

To compute its similarity dimension \( D \) , it is notable that \( {f_{1}} \) and \( {f_{2}} \) are not only contractions with factors \( λ_{1} \) = \( \frac{1}{S}, λ_{2} \) = \( \frac{1-a}{as} \) but also similarities in the sense that \( |{f_{i}}(x)-{f_{i}}(y)|= {λ_{i}}|x-y| \) for any pair of points \( x \) and \( y \) in the interval [0,1].

Recall the defining equation:

\( λ_{1}^{D}+λ_{2}^{D}=1, \)

whose unique solution \( D \) is the similarity dimension of \( P \) . As \( D \) is nonzero and strictly smaller than 1, it is concluded that \( P \) is a fractal with non-integer dimension.

Next this paper shows that the dynamics of \( T \) on \( P \) is chaotic in the sense that there is a dense orbit, and the periodic orbits form a dense set. For this, the author considers the sequence space \( \sum _{2}^{+}=\lbrace {s_{0}}{s_{1}}{s_{2}}.....|{s_{i}}∈\lbrace 1,2\rbrace \rbrace \) and define the coding map h : \( \sum _{2}^{+}→P \) by h(s) \( \underset{n→∞}{lim} {f_{{s_{0}}}}∘⋯∘{f_{{s_{n}}}}([0,1]) \) . Note that this limit exists and is unique because \( {f_{1}} \) and \( {f_{2}} \) are both contractions on the interval [0,1]. By the nested property of \( {I_{{s_{0}}....{s_{n-1}}}}{f_{{s_{0}}}}∘⋯∘{f_{{s_{n-1}}}} \) ([0,1]), it follows that \( {h(s)∈I_{{s_{0}}....{s_{n-1}}}} \) for any \( n \) .

Moreover, for every point \( x∈P \) there is a unique symbolic sequence \( s∈Σ_{2}^{+} \) for which \( h(s)=x \) . The dynamics of \( T \) on \( P \) can be represented by the shift dynamics \( σ \) on \( Σ_{2}^{+} \) in the sense that \( T h(s)=h∘σ(s) \) , where \( σ({s_{0}}{s_{1}}⋯)={s_{1}}⋯ \) .

For the first property of chaos, this paper constructs a point x \( ∈P \) whose orbit under \( T \) is dense in \( P \) . It is notable that a set is dense in \( P \) if and only if it contains a point in \( {I_{{s_{0}}....{s_{n-1}}}} \) for every possible finite symbolic sequence \( {s_{0}}⋯{s_{n-1}} \) . Therefore, it suffices to construct a symbolic sequence \( s \) containing all possible finite symbolic sequence \( {s_{0}}⋯{s_{n-1}} \) . For instance, such a sequence can be obtained by listing consecutively all finite sequences.

For the second property of chaos, in each \( {I_{{s_{0}}....{s_{n-1}}}} \) a periodic point under iterates of \( T \) is exhibited. Note that a point \( x∈P satisfies {T^{m}}(x)=x \) if and only if there is some symbolic sequence \( s∈Σ_{2}^{+} \) such that \( x=h(s) \) and \( {σ^{m}}(s)=s \) . Hence, it suffices to exhibit a periodic symbolic sequence that begins with \( {s_{0}}⋯{s_{n-1}} \) : \( {s=s_{0}}⋯{s_{n-1}}{s_{0}}⋯{s_{n-1}}⋯ \) .

3. Conclusion

This essay explores the connection between chaos and fractals, specifically focusing on the concept of a fractal repeller. For a more concrete example, let’s examine the mapping of a line described by formula (1), assuming that the parameters meet the condition \( a∈(0,1) ; sa \gt 1 \) . And the paper examines the evolving role of the image. This essay demonstrates the strong correlation between chaos theory and fractal theory. Understanding the intricate dynamics of complex systems and the presence of self-similarity in various natural and man-made systems is a fascinating aspect of scientific exploration. Through exploring the relationship between chaos and fractals, we can gain a deeper understanding of the governing principles behind natural phenomena and complex systems. This knowledge can offer fresh insights and approaches for advancements in the fields of science and engineering. Future research can delve deeper into the intricate connections between chaos and fractals and their potential applications across various disciplines, thereby advancing our comprehension and mastery of intricate systems.