1. Introduction

With finance and economics constantly evolving, making accurate predictions about complex systems is a must for those analyzing stock market behavior, forecasting economic indicators such as exchange rates and inflation, as well as evaluating the impact of policies. Two commonly used methods in these fields are regression analysis and autoregressive integrated moving average (ARIMA) models. Under these approaches, the accuracy of conclusions drawn from a model heavily relies on the validity of the model assumptions. Many models of stock returns assume that these returns are random, which is essential for deriving useful information from the data. In addition to studying the distribution of returns, model validation often involves looking at residuals, which are simply differences between observed values and values predicted by the model. The key is that these residuals should be random. The White Noise Hypothesis Test is an excellent tool for analyzing residuals and determining whether they are random or contain patterns and correlations. By testing these patterns, analysts can check whether their models are valid, based on the two key assumptions of regression analysis, and determine whether they have captured all the useful information about the system under study. In this paper, we discuss the use of the White Noise Hypothesis Test in stock market analysis, risk management, economic forecasting, policy analysis, and other applications where prediction of future events or outcomes is important [1]. We illustrate the use of the test by solving a number of simulated examples.

2. Regression Analysis

2.1. Residual Independence

This assumption of independence of residuals extends to the mathematical basis upon which the regression models themselves are defined, and a regression model will reliably give valid parameter estimates and hence valid model prediction and model-based hypothesis tests only if this assumption is satisfied. Violation of the independence assumption implies serial correlation, by which is meant that the error in one observation is related to the error in another, and this serial correlation can severely distort estimates. The dependence of valid model-based inference on the assumption that the residuals are independently distributed is such an important issue that statistical packages include the White Noise Hypothesis Test to assess whether they are or not. The Durbin-Watson statistic and similar techniques measure the amount of correlation between the residuals and detect any pattern in the residuals that is not commensurate with randomness. When such a pattern is detected, this implies that the model does not capture all the information in the data, hence the results of modelling it are unreliable, and further work on specifying the model is required to reduce or eliminate the serial correlation, through adding lagged variables, for example, or reconsidering the model structure [2].

Regression analysis uses the Durbin-Watson (or DW) statistic to test for residual independence when it is time-ordered data by calculating serial correlation in the residuals

\( DW=\frac{\sum _{i=2}^{n}{({ε_{i}}-{ε_{i-1}})^{2}}}{\sum _{i=1}^{n}ε_{i}^{2}}\ \ \ (1) \)

This statistic provides a measure of the correlation between residuals, with values close to 2 indicating independence and deviations suggesting potential serial correlation that may require model refinement.

2.2. Homoscedasticity

Homoscedasticity is the assumption that the variance of the residuals remains constant across all values of the independent variables. It is important in the regression context because it means that the model makes equally accurate predictions across the range of the data, and unrestricted heteroscedasticity allows for inefficiencies and/or biases in parameter estimation. When heteroscedasticity is present, the predictive precision of the least squares estimators is compromised, leading to biased standard errors for the estimates, and (sometimes) misleading results in hypothesis testing. Heteroscedasticity can be assessed using a White Noise Hypothesis Test, with either the Breusch-Pagan test or White’s test being commonly used to determine whether the variance of the residuals tends to vary across the range of values of the independent variable [3]. When heteroscedasticity is present, it is possible to handle such instances when estimating the parameters with variables that may be transformed to address the issue (such as the logarithmic transformation), using weighted least squares, or when none of the other approaches are viable, one can use robust standard errors.

2.3. Model Fit and Adequacy

Furthermore, in addition to evaluating residual independence and homoscedasticity of the regression model, the White Noise Hypothes in evaluating whether the model fits the data ade call its ‘goodness, the fit of the model is assessed using the standard metrics such as R-squared and adjusted R-squared, which assess what proportion of the variance in the dependent variable the model accounts for. However, these metrics ignore serial correlation (or heteroscedasticity) in the model residuals, and so do not detect systematic patterns (or lack thereof) in the residuals that might reflect model mis-specifications. Often, however, as one investigates the residuals more closely, they detect patterns or lack thereof that could be interpreted as model mis-specifications, which leads to running the model again, this time with additional terms, such as interactions, squared terms (ie, polynomials), or transformations of the data [4]. In other words, analysts can use insights gleaned from residual analysis to improve the accuracy and robustness of their models.

3. ARIMA Models

3.1. Residual White Noise Testing

The White Noise Hypothesis Test of the residuals is a critical step to making the ARIMA model, since it confirms that the residuals from a fitted model do in fact display white-noise properties. The ARIMA model, which contains both an autoregressive (AR) and a moving-average (MA) component, has the assumption that, after you fit the model, the residuals will be uncorrelated and homoscedastic - that is, close to a white-noise process. This is one indicator that all the available patterning in the time series is explained by the fitted ARIMA model. The White Noise Hypothesis Test of the residuals, such as the Ljung-Box test, checks to make sure that the residuals do not display autocorrelation or other non-random patterns. If the residuals do not produce white noise, this is a sign that the data’s temporal dependencies are not well-captured, and that you need to further tweak your model. You might want to re-fit the AR, MA, and/or seasonal order of your model. You might also want to difference the data (ie, the unit root test) if it is still non-stationary. In any case, you want to make sure that the residuals are white noise, or else you cannot be fully confident in the adequacy of your model -and thus of your forecasts [5].

The Ljung-Box test is used to check if the residuals of an ARIMA model are autocorrelated or show other non-random patterns, to test whether the residuals are white noise, represented by this statistic:

\( Q=n(n+2)\sum _{k=1}^{h}\frac{\hat{ρ}_{k}^{2}}{n-k}\ \ \ (2) \)

This statistic assesses the independence of residuals, with larger values indicating that the residuals are not white noise, which may require further model refinement [6].

3.2. Model Selection and Diagnostics

Coupling the appropriate ARIMA model with the data is a key step in time series analysis, which determines whether the chosen model captures the underlying dynamics of the data with sufficient accuracy. Model selection is a process that typically involves the comparison of different ARIMA specifications using criteria such as the Akaike Information Criterion (AIC) or Bayesian Information Criterion (BIC), which are both criteria balance fit and complexity. In this process, the WNHT plays a vital role by examining the adequacy of different models. The examination of the properties of the residuals will shed light on whether they were produced by a model that successfully nails the dynamics of the data. The WNHT serves as a diagnostic check that enhances the model selection criteria procedure by ensuring that the model produces residuals that are independent and free from any systematic patterns. This iterative process of model selection, estimation and validation produces a parsimonious and accurate ARIMA model with sufficient predictive ability and provides insights into the future of the time series of interest.

3.3. Improving Model Performance

So we need to continuously monitor the residuals from a fitted ARIMA model via the White Noise Hypothesis Test, so that we can revisit our model and see whether no systematic changes or drifts have occurred since the last fit, potentially tweaking the model (and the forecasters themselves) to improve performance. It can be a hard lesson for new time series analysts to learn, but if the residuals stop looking like white noise, it can help to reconsider the adequacy of the model or the structure of the underlying time series dynamical process. For example, if the residuals begin to exhibit a different autocorrelation structure than expected, it could be a cue to come up with a different model structure. Re-estimation of the model parameters or the inclusion of additional explanatory variables might be necessary. It could also be that the original time series itself underwent a structural change, drift or shift relative to the model, necessitating maintenance to sustain the model’s performance over time. Like any mathematical or statistical model that aims to capture the essence of noisy process data that can be unpredictable because they evolve over time, it’s important to provide for allowing the model some degree of ‘breathing room’, rather than insisting that the actual data have to obey a model’s strict assumptions and expectations [7].

4. Applications in Finance

4.1. Stock Market Analysis

In finance, regression analysis and ARIMA models are used to analyse stock market behaviour to predict future prices. The White Noise Hypothesis Test helps in the validation of these models to see if residuals have patterns that could lead to incorrect conclusions about predictive accuracy. The stock market is by definition factors, including economic indicators, geopolitical events and investor sentiments. By using the White Noise Hypothesis Test, analysts can make sure their models, such as the ones to analyse stock prices or returns, are not missing any information. This is an indication prices fully reflect all available information. Models that have residuals that appear to be similar to white noise would indicate that price changes are random and cannot be predicted – market efficiency and the Efficient Market Hypothesis (EMH) would then be confirmed. The use of white noise tests for the validation finance models would help analysts have confidence in their ability to detect trends, assess risks and make the right investment decisions that are guided by market dynamics and investors’ objectives [8]. Table 1 is a simulated analysis of stock market behaviour using regression analysis and ARIMA models. The table helps us assess whether models capture the dynamics of the stock market.

Table 1. Stock Market Analysis Using White Noise Hypothesis Test

4.2. Risk Management

The accurate modelling of such a financial time series is critical for effective and precise risk management. Models are used by financial institutions to assess market risks as well as interest rate fluctuations, volatility and credit risk. The White Noise Hypothesis Test is used to assess if the residuals have the characteristics of white noise, which indicates that the model captures most of the relevant risk factors. If a model passes the white noise test, then it is appropriate to use the model to evaluate its ability in identifying potential risk exposures and form the strategic risk management decisions. This part illustrates how to prevent the risk models from missing some crucial information that could affect the predictive accuracy of the model. The white noise tests used to validate the models could help the risk managers to form a better prediction in the markets, seek for and hence enhance the stability in financial systems over the whole economic cycle. Figure 1 shows the percentage of models passing the white noise test and those failing it [9]. It suggests that those models passing the white noise test are appropriate to be used for risk management.

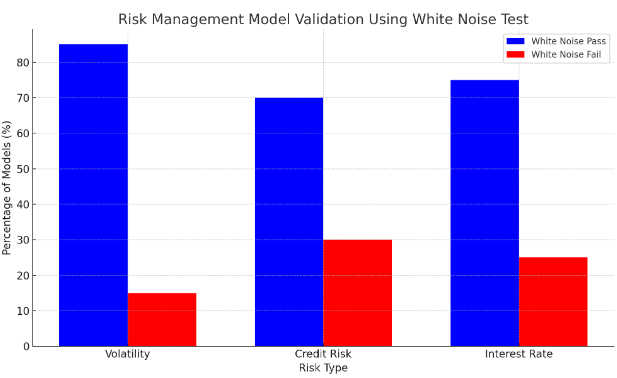
Figure 1. Risk Management Model Validation Using White Noise Test

5. Applications in Economics

5.1. Economic Forecasting

Several of the most common models used by economists to forecast key indicators such as GDP growth, inflation or unemployment rates are traditional ARIMA models. Policymakers, business and investors depend on their predictions to make decisions about the future course of the economy. For this reason, it is essential that these models’ predictions are accurate. This is where the White Noise Hypothesis Test comes into play: by establishing whether a model’s residuals exhibit autocorrelation or any other pattern that would compromise its forecasting reliability. A model that passes the white noise test is one in which its predictions are less likely to be skewed by any non-random pattern in the residuals; it is the outcome of a model that has been able to capture the underlying dynamics of the economic series under consideration. As we have seen, the white noise test is used to evaluate the fit of a model to an economic series. A validated model is one that entails more credible predictions for future economic conditions [10]. By ensuring that models meet the criteria of white noise, forecasters are providing more accurate predictions that help followers of the economic process make better policy and business decisions based on expected future economic conditions.

5.2. Policy Analysis

One important application is in policy analysis, where regression models are used to estimate the effects of different interventions and reforms on various economic and social outcomes. Policymakers and researchers rely on estimated models to evaluate interventions, such as tax reforms, subsidy programmes or regulatory reforms, to determine their effectiveness. If the core assumptions of the models – that the residuals are independent across individuals and homoscedastic across the sample – are falsified, then the results of these models cannot be trusted, and they become potentially useless for policy inferences. Models that pass the White Noise Hypothesis Test suggest that the policy instruments observed in the data have been sufficiently modelled in the regression equation, and that the residuals ‘look like white noise’, which therefore confirms the absence of bias in the model estimates.

6. Conclusion

The White Noise Hypothesis Test is therefore a crucial tool in validating statistical models in the context of financial and economic analysis, thereby leading to more credible and robust predictions. Confirming the independence and homoscedasticity of regression analysis residuals, and ensuring that the residuals of an ARIMA model are truly white noise, analysts can boost the integrity of models used for various financial and economic applications including stock analysis, economic forecasting and policy evaluation. Through the systematic application of white noise tests, analysts have the opportunity to detect model inadequacies and provide more reliable predictions that will impact future investment decisions. In an era where financial and economic systems are becoming increasingly more integrated, the adoption of white noise tests in processes of model validation represents an important step forward in strengthening the epistemic foundations of modelling, thereby allowing for better detection of destabilizing processes in uncertain environments.