1. Introduction

Quantum Neural Networks (QNNs) are a new paradigm in machine learning due to the convergence of quantum computing and neural networks. Image recognition, natural language processing, and game play are some of the domains where traditional neural networks have achieved remarkable success. However, they are limited by the inherent constraints of classical computation, particularly in handling exponentially large data spaces and complex optimization problems.

Quantum computing, which has superposition, entanglement, and quantum parallelism, provides a viable alternative to these limitations. By leveraging quantum mechanics, QNNs have the potential to perform computations that are infeasible for classical systems, enabling significant advancements in speed and efficiency.

The objective of this paper is to give a complete overview of QNNs, beginning with their theoretical underpinnings and extending to practical implementations. We will explore different QNN architectures, including fully quantum and hybrid quantum-classical models, and examine their performance on various machine learning tasks. Additionally, we will address the current challenges in the field, such as error correction, decoherence, and scalability, and propose potential future research directions.

By bridging the gap between quantum computing and artificial intelligence, QNNs represent a transformative step towards the next generation of intelligent systems. This paper seeks to highlight their importance and potential impact, providing a roadmap for researchers and practitioners in both fields.

2. Conceptions

2.1. Quantum Computing

Quantum computing is heavily reliant on the quantum bit, or qubit, which is the fundamental unit of quantum information. Classical bits can only be one of the 0 or 1 states. However, in quantum computing, information can be recorded as |0⟩, |1⟩, or quantum states which use them as base vectors. Two-dimensional complex Hilbert Spaces can be used to represent qubits.

In classical computing, a bit occupies a single state at any moment. Conversely, in quantum computing, a qubit can simultaneously exist in state 0, 1, or any linear combination of them. When measured, this superposition collapses, with the final state determined by the probability distribution of qubit states. Quantum superposition thus allows qubit to be in multiple states at once until measurement.

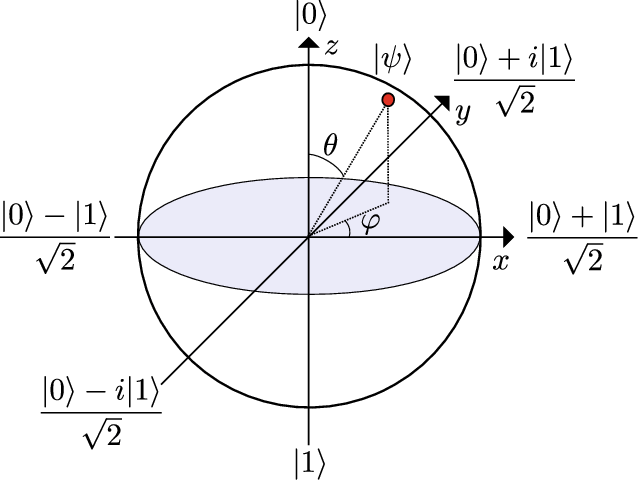
Figure 1. The Bloch Sphere Representation of a Qubit State [1]

As Figure 1 shows, this is visually represented on the Bloch sphere, where a qubit's state is depicted as a point on the surface of the sphere. The position of this point is determined by the angles θ and φ, which correspond to the probabilities of the qubit being in a particular state. The Bloch sphere representation is particularly useful for understanding quantum operations and the effects of quantum gates on qubits, as it provides a clear geometric interpretation of these complex quantum phenomena.

When two or more particles are linked, quantum entanglement is a phenomenon where one qubit's state is dependent on the state of the other qubit. All the other qubits in an entangled system are affected if one qubit's state changes.

Quantum gates form the foundational components of quantum circuits. These gates modify the states of qubits and are usually depicted by unitary matrices. Owing to quantum mechanical principles like superposition and entanglement, quantum gates can execute intricate operations.

Figure 2 lists some basic quantum gates. The Pauli-X gate (NOT gate), flips the state of a qubit. It changes |0⟩ to |1⟩ and |1⟩ to |0⟩. The Pauli-Z gate applies a phase flip, which leaves |0⟩ unchanged and maps |1⟩ to -|1⟩. The Hadamard gate is a quantum gate that transforms a qubit into an equal superposition of its basis states, creating a state where the qubit has an equal probability of being measured as 0 or 1. The T Gate (π/8 Gate) applies a phase shift of 𝜋/4, it leaves |0⟩ unchanged and maps |1⟩ to \( {e^{iπ/4}} \) |1⟩. The CNOT gate flips the state of the target qubit if the control qubit is in the |1⟩ state. It is essential for creating entanglement between qubits. The SWAP gate can swap the states of two qubits. If the first qubit is in state |a⟩ and the second in state |b⟩, after the SWAP gate, the first qubit will be in state |b⟩ and the second in state |a⟩ [2].

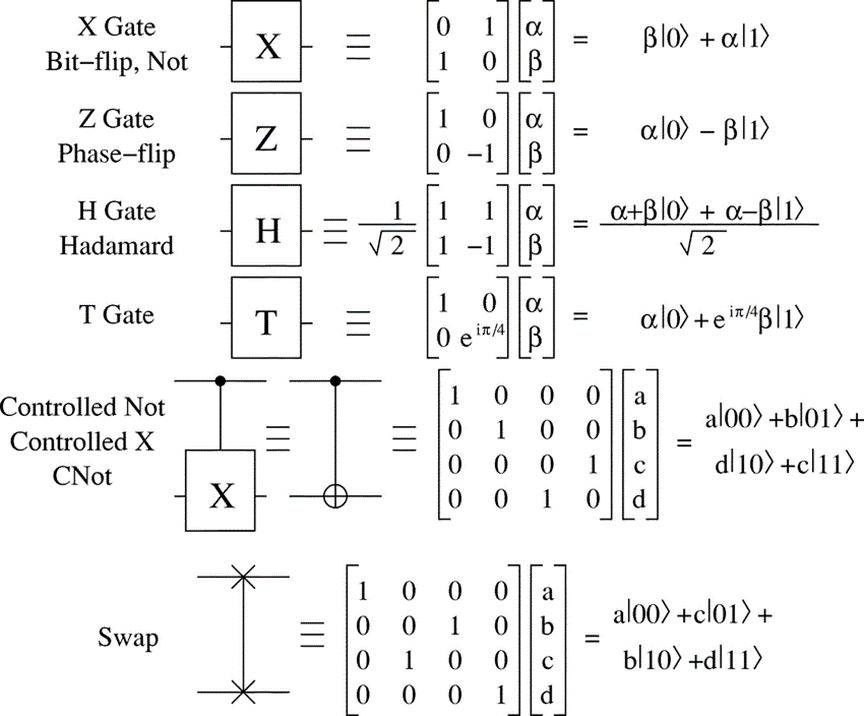
Figure 2. Basic Quantum Gates and Their Matrix Representations [3]

Quantum circuits are composed of sequences of quantum gates. E Each quantum circuit is a quantum algorithm that can solve complex problems with greater efficiency than classical algorithms. To achieve desired quantum state transformations, quantum circuits must be constructed by ordering quantum gates in a specifically.

The design of quantum circuits requires careful consideration of the order and type of gates used, as each gate affects the qubits in a unique way. For instance, a phase shift introduced by a Z gate can alter the phase relationship between qubit states, which is crucial for certain quantum computations like quantum Fourier transforms. Furthermore, error correction protocols often incorporate additional gates and ancillary qubits to protect against decoherence and other quantum noise, ensuring the reliability of the circuit.

2.2. Classical Neural Networks

Classical neural networks (NNs) are the cornerstone of modern artificial intelligence and machine learning. Neurons are the basic units of neural networks. Each neuron receives input, processes input, and produces output. The basic structure of neurons includes input layer, weight, bias, activation function and output. The weight determines the strength of the connections between neurons, while the bias is used to adjust the weighted sum of the output and input.

The typical structure of a neural network consists of multiple layers: an input layer, one or more hidden layers, and an output layer. The input layer receives and processes the raw data, the hidden layer transforms this data through multiple operations, and the output layer provides the final output. These networks can range from direct feedforward structures to more complex configurations such as convolutional neural networks (CNNS) and recurrent neural networks (RNNS).

In the process of training the neural network, the weights and biases need to be adjusted to minimize the output error. This is usually achieved by backpropagation. Optimization algorithm is also an important part of neural network training. Gradient descent is the most commonly used technique by adjusting the model parameters along the negative gradient direction of the loss function. Variants of gradient descent, such as Stochastic gradient Descent (SGD), RMSprop, and Adam, offer improvements in speed of convergence and stability [4].

3. Quantum Neural Networks (QNNs)

Combining these two concepts, quantum neural networks (QNNs) represent the frontier of combining quantum computing and neural networks, aiming to enhance computing power by quantum mechanics principles.

Quantum neural networks (QNNs) integrate quantum computing principles into neural network frameworks. Qubits can exist in superposition, representing both 0 and 1 simultaneously, and can also become entangled with each other, creating intricate associations that classical neural networks are unable to replicate. These features enable QNNs to perform parallel computing on an unprecedented scale, providing significant acceleration on certain types of problems.

The fundamental architecture of a QNN is comparable to that of a conventional neural network, but it employs qubits and quantum gates instead of conventional bits and logic gates. A typical QNN consists of quantum neurons that process information by a unitary transformation that preserves the probability amplitude. Common quantum gates in QNN include Hadamard gates, CNOT gates, and Pauli-X gates, which are used to manipulate qubits to perform necessary calculations in the network.

Quantum neurons can represent and process information in ways that classical neurons cannot. For example, the principle of quantum parallelism makes quantum neuron be able to process multiple input states concurrently. The architecture of QNN can vary, but common models include quantum feedforward neural networks and quantum convolutional neural networks [5].

Mathematically, if you consider a quantum neuron, it can be expressed as |ψ_out⟩=U|ψ_in⟩, where |ψ_in⟩ is the input quantum state, |ψ_out⟩ is the output quantum state, and U is a unitary operator acting on the input state.

Quantum states in QNNs allow for superposition, enabling parallel processing beyond classical bits. Quantum gates manipulate these states to perform calculations. Entanglement links qubits, allowing them to influence each other over long distances, creating highly interconnected networks that solve complex problems more efficiently.

For instance, the application of a Hadamard gate (H) to a qubit in state \( |0⟩ \) creates superposition as:

\( H|0⟩=\frac{1}{\sqrt[]{2}}(|0⟩+|1⟩) \) (1)

This superposition state can then be entangled with another qubit using a CNOT gate, creating an entangled pair:

\( CNOT(\frac{1}{\sqrt[]{2}}(|0⟩+|1⟩)⊗|0⟩) = \frac{1}{\sqrt[]{2}}(|00⟩+|11⟩ \) ) (2)

The application of quantum states and operations in neural networks offers new opportunities for solving problems in various domains, from optimization to pattern recognition.

4. Design and implementation of QNNs

Quantum neurons are the basic elements of QNN. They manipulate qubits and do calculations using quantum gates. The design of quantum neurons involves defining unitary operations that can transform the input quantum state into the desired output state. Quantum activation functions are similar to classical activation functions, but need to adapt to the properties of quantum states, usually through unitary transformations.

For example, a quantum neuron might use a combination of Hadamard and Pauli-X gates to create a non-linear transformation: U=H⋅X, (H is Hadamard gate and X is Pauli-X gate). This combination can create complex transformations necessary for processing quantum information.

The quantum layer of a QNN is composed of multiple quantum neurons. The input qubits are processed by a set of quantum operations by each layer, converting them into output qubits. Quantum weights are used to adjust the magnitude and phase of qubits to optimize network performance. Unlike classical weights, quantum weights need to be managed in a way that preserves the coherence of the quantum states.

Mathematically, a quantum layer can be represented as |ψ_out⟩=U₂U₁|ψ_in⟩, where U₁ and U₂ are unitary operators representing the transformations applied by the neurons in the layer.

Training QNN involves optimizing quantum weights to minimize errors in the network output. Due to the nature of quantum data and operations, this process is much more complex than training classical neural networks. The quantum training algorithm uses the superposition and entanglement characteristics of quantum to search the parameter space efficiently and find the optimal solution.

Quantum gradient descent (QGD) is an adaptation of the classical gradient descent algorithm in quantum systems. The process entails calculating the slope of the quantum loss function with respect to the quantum weights and iteratively changing those weights to decrease the loss. The challenge is to efficiently calculate these gradients while maintaining the coherence of quantum systems [6].

In QNN, the loss function L is defined as:

\( L = ⟨{ψ_{out}}|\hat{O}|{ψ_{out}}⟩\ \ \ (3) \)

Where \( \hat{O} \) is the observable quantity relevant to the task. Gradient descent update rules are as follows:

\( w_{ⅈj}^{(t+1)}=w_{ⅈj}^{(t)}-η\frac{∂L}{∂{w_{ⅈj}}} \) (4)

where η is the learning rate and w_ij are the quantum weights.

Quantum backpropagation is the quantum equivalent of a classical backpropagation algorithm. It involves backpropagating the error gradient through the network to update the quantum weights. This process uses quantum gates to calculate the gradient and make the necessary adjustments to the quantum state [7].

Quantum backpropagation can be formulated using the adjoint of the quantum operations:

\( {δ_{i}}=U_{i}^{†}{δ_{i+1}}{U_{i}} \) (5)

where \( {δ_{i}} \) represents the error term at layer i, and \( U_{i}^{†} \) is the adjoint (inverse) of the unitary operator \( {U_{i}} \) .

5. Advantages of QNNs

An immediate advantage of quantum computing is its potential speed. Qubits can exist synchronously in superpositions of multiple states, so quantum computing can process data in parallel. In contrast, classical computing requires processing each state sequentially. In QNNs, this parallel processing capability is used to accelerate the training and reasoning process of neural networks.

According to some studies, quantum computing could theoretically achieve an exponential speed increase when solving certain optimization problems. For example, the Shor algorithm is several orders of magnitude faster than the best classical algorithms on prime factorization problems [8]. This means that in the training of large data sets and complex models, QNNs can significantly reduce computation time and thus improve efficiency. Results show that the quantum variational optimization algorithm (VQA) is more efficient than the classical algorithm when dealing with complex optimization problems, particularly in image segmentation. This efficiency boost is important for deep learning tasks that require a lot of computing resources.

Another significant advantage of quantum computing is its energy efficiency. The parallel processing capabilities of quantum computing make it consume much less energy than classical computing for the same computational task. For example, quantum circuits can perform complex matrix operations with low energy consumption, which is particularly important in large-scale neural network training. The high energy efficiency of quantum computing not only helps to reduce energy consumption but also can significantly reduce computing costs.

High-dimensional data processing is a key challenge in modern machine learning and data science. When dealing with high-dimensional data, traditional neural networks often face the problem of dimensional disaster, that is, the computational complexity increases exponentially with the increase of data dimensions. Quantum computing can process data more efficiently in high-dimensional space.

The superposition property of quantum states allows qubits to represent multiple states simultaneously, allowing for parallel computation in high-dimensional Spaces. For example, in quantum states, a system of n qubits can represent 2^n states. This capability allows QNNs to significantly reduce computation time when working with high-dimensional data.

Another advantage of quantum computing when dealing with high-dimensional data is its ability to perform dimensionality reduction and feature selection operations efficiently. The optimal feature subset can be quickly found in the high-dimensional space, thus improving the efficiency and accuracy of data analysis. For example, techniques such as quantum state projection and quantum Fourier transform (QFT) are widely used in quantum feature selection [9].

Quantum parallelism allows quantum neural networks to inspect multiple possible solutions simultaneously, resulting in significantly improved computational efficiency. Quantum parallelism is achieved through the superposition of qubits, allowing multiple computation paths to occur simultaneously. This property is particularly important when training and reasoning large neural networks.

Specifically, quantum parallelism can improve the performance of QNNs at multiple levels. For example, during training, quantum gradient descent algorithms can compute multiple gradients simultaneously, thus speeding up the convergence process. In reasoning, quantum parallelism can speed up the prediction process and improve real-time processing power.

Quantum parallelism also plays an important role in optimization algorithms. Algorithms such as quantum particle swarm optimization and quantum genetics, for example, greatly improve optimization efficiency and accuracy by exploring multiple parallel solution Spaces.

6. Applications

Quantum Neural Networks (QNNs) represent a significant advancement in artificial intelligence by integrating quantum computing principles with classical neural network frameworks. This synthesis offers potential improvements across various domains, including image recognition, natural language processing (NLP), financial forecasting, and bioinformatics.

Quantum Convolutional Neural Networks (QCNNs) leverage quantum computing's parallelism to process image features simultaneously, enhancing accuracy and reducing computational demands. Study [10] have shown QCNNs' superior performance in tasks like CT scan image classification, demonstrating higher accuracy than classical CNNs.

In NLP, QNNs utilize quantum superposition and entanglement to manage complex linguistic relationships, benefiting tasks such as sentiment analysis and machine translation. Research by Ravikumar et al. [11] has indicated that QNNs improve processing speed and accuracy, especially with large datasets.

QNNs' capability to handle extensive financial data enables more accurate market trend predictions and risk management. El Bouchti et al. [12] and E. Paquet et al. [13] highlighted the efficiency of QNNs in financial forecasting, with notable improvements over classical approaches.

In bioinformatics, QNNs enhance the analysis of biological data, such as genetic sequences. The study by Tao et al. [14] introduced Quantum Bound, a hybrid neural network that integrates classical and quantum elements, optimizing the analysis of complex biological datasets.

7. Conclusion

Quantum Neural Networks (QNNs) represent a significant leap in the fusion of quantum computing and artificial intelligence, offering unparalleled computational capabilities. By leveraging quantum superposition and entanglement, QNNs can execute complex calculations and data processing tasks more efficiently than classical neural networks. This integration enhances the accuracy and speed of large-scale data analysis, making QNNs valuable for applications in finance, healthcare, and other fields.

The development and implementation of QNNs require interdisciplinary collaboration across quantum physics, computer science, and domain-specific expertise. Educational programs and industry-academia partnerships are vital for advancing QNN research and ensuring practical application. Promoting open science and data sharing can further accelerate innovation and prevent redundant efforts.

Future directions for QNNs include the development of hybrid quantum-classical systems, improved quantum hardware, and new quantum algorithms. These efforts aim to maximize performance and reliability. Additionally, addressing the ethical and societal implications of QNNs, such as data privacy and job displacement, is crucial for their responsible deployment.

In summary, the potential of QNNs is immense, promising significant advancements in computing and various application domains. Overcoming technical challenges and fostering interdisciplinary cooperation are key to realizing their full potential.