1. Introduction

With the advent of the big data era, vast amounts of data have generated numerous high-dimensional datasets, which are prevalent across various industries. To maintain data integrity and prevent the loss of important information during transmission or utilization, the raw data presented to decision-makers as reference often contains a large amount of redundant information and attributes unrelated to the current decision-learning task. These redundant data and irrelevant attributes not only reduce the accuracy of decision-making but also increase the time and spatial complexity of learning algorithms. Therefore, before conducting effective research using these high-dimensional datasets, it is necessary to perform dimensionality reduction on their attributes and features. The purpose of feature selection is to select a subset of relevant features from the original dataset that are related to the study, thereby constructing a new feature subset. This reduces learning time while ensuring that the set performance indicators are optimized [1]. As a data preprocessing technique, feature selection algorithms have been widely applied across various industries. Their integration with industries has solved numerous practical problems, such as traffic classification in the smart Internet of Things [2], band selection in remote sensing images [3], wide-area motion image registration in aviation [4], and video semantic recognition [5].

Due to its ability to explore optimal or near-optimal solutions through global search strategies, evolutionary feature selection has become a popular technique for solving feature selection problems in recent years [6]. Among many algorithms, the Particle Swarm Optimization (PSO) algorithm, as a relatively novel evolutionary optimization technique, has been applied to feature selection problems due to its simplicity, ease of implementation, and fast convergence speed [7,8].

The PSO algorithm was developed by Kenney and Eberhart in the 1990s, inspired by bird flocking behavior. The basic principle of the algorithm is to define a vector space for decision-making, then randomly distribute the individual particles (samples) within this space. These particles simulate the foraging behavior of birds, searching for optimal solutions by flying through the space based on specific mechanisms. In each iteration, particles calculate their fitness based on a fitness function, and through ranking, the best position in space is determined to find the optimal solution. Due to its convenience and few parameters, PSO has been widely applied in academia. However, when seeking global optimal solutions in practice, it is crucial to consider both global and local search capabilities. To enhance the applicability of the PSO algorithm, various improvement strategies have been proposed. Notable variants include the KPSO algorithm, DPPSO algorithm, among others. In 2002, Agrafiotis [9] was the first to apply PSO to feature selection problems, and since then, many PSO-based feature selection algorithms have emerged. With the rapid growth of big data and the sharing economy, evolutionary optimization with global search capabilities has been applied to distributed feature selection, significantly improving the algorithm's global search performance.

Given the limitations of the PSO algorithm in some scenarios, and to address the needs of this study, we introduced the PSO-SVM algorithm.

The PSO-SVM algorithm was developed by Cortes and Vapnik in 1995 [10] as a supervised learning model rooted in statistical learning theory. It has become an important tool for solving classification and regression problems in the fields of machine learning and data mining. The core concept of the SVM is to identify and establish the optimal classification boundary, achieving efficient classification with excellent generalization capabilities and high accuracy.

Building on this, Suykens further developed the Least Squares Support Vector Machine (LS-SVM) in 2001 [11]. This variant innovatively replaced the traditional inequality constraints in SVM with equality constraints, significantly simplifying the solution process, albeit at the cost of sacrificing some of the model's sparsity.

Internationally, financial risk prediction has become one of the prominent applications of LS-SVM. Kim (2003) [12] successfully introduced SVM into stock price index prediction, validating the feasibility and potential of SVM in financial forecasting. Subsequently, Lee (2006) [13] expanded its application to corporate credit rating prediction, showcasing the wide application prospects of SVM in credit evaluation. Ahn et al. (2010) [14] used the SVM algorithm in constructing a financial crisis early warning system, and their research confirmed the effectiveness and value of SVM as a financial risk warning model.

Compared to the PSO algorithm, introducing SVM enhances parameter optimization, eliminating the complexity and subjectivity of manually adjusting parameters and thereby improving prediction accuracy. Additionally, SVM reduces the search space, and combined with parallel computing, it boosts algorithm efficiency and accelerates model training. Thanks to the inherent flexibility and adaptability of the SVM algorithm, these improvements lead to automated parameter tuning, achieving a higher level of intelligence and automation.

To further extract the importance of feature variables, LightGBM machine learning model was introduced.

LightGBM is a machine learning model based on gradient boosting decision trees. Its key advantages include fast training speed, low memory consumption, and high accuracy. LightGBM uses a split-based benchmark and a histogram algorithm, which optimizes the time complexity of the splitting process, allowing the model to efficiently learn and handle large datasets. By integrating local histogram optimization and exclusive feature bundling techniques, LightGBM can more intelligently manage and process features, enhancing the model’s overall performance.

The main principles of LightGBM can be divided into two aspects: finding the optimal split point and learning the tree structure using a leaf-wise growth strategy. In finding the optimal split point, LightGBM uses a histogram technique that classifies data based on features, with each class storing a set of samples. For each class, internal sample statistics are collected, and gradient information is used to construct histograms. The accumulated histograms are then used to calculate the gradient information sum for the left and right classes at a given point, reducing computational complexity. Additionally, difference acceleration is used to improve the running speed. After constructing the child leaf histograms, LightGBM performs a subtraction operation between the parent and child histograms to obtain the histograms for other child leaves.

The leaf-wise growth strategy refers to how LightGBM grows the tree. Unlike the commonly used layer-wise growth algorithm, LightGBM adopts a leaf-wise growth algorithm with depth constraints. In this algorithm, only the leaf with the highest split gain is split, unlike layer-wise growth where all nodes are split. To prevent potential overfitting, a maximum depth constraint is added when splitting the leaf. As a result, compared to the layer-wise growth algorithm, the leaf-wise growth strategy can improve the model’s accuracy with the same number of splits.

2. Research Design

2.1. Data Source

The data for this study is sourced from user reviews automatically collected by an online platform system. In the PSO algorithm, each particle is considered an independent search entity within the search space. When a particle is located at the best historical position, assisting the swarm in finding the global optimal position, it dynamically adjusts its velocity. Based on this algorithm, platform-sharing economy consumption characteristics are identified through the following dimensions: Perceived Transaction Cost (CP), Breach Penalty (CB), Convenience (CC), Willingness to Pay (BP), Personal Privacy (SP), and Civility (MP). The predicted variable is the willingness to participate in the sharing economy (where 0 represents no willingness and 1 represents willingness). The advantage of the PSO algorithm lies in its ability to comprehensively consider the interactions between different feature units, simulating the movement between multiple features to achieve global optimization, thereby producing more accurate results. The basic description of the experimental data is shown in Table 1.

Table 1. Data Source

2.2. Methods

2.2.1. PSO-SVM

The introduction of SVM is primarily based on its ability to effectively classify data while ensuring that the separating hyperplane maintains the maximum possible distance from other features. The penalty parameter C and the kernel function parameter σ significantly influence the final prediction results.

In the PSO-SVM hybrid algorithm, multiple particles are first randomly generated, represented by m, forming the initial population X = (X1, X2, …, Xm). X represents vectors in the N-dimensional Euclidean space, and each particle corresponds to a class label yi, where yi ∈ {−1, 1}, thus forming the training set (xi, yi). xi represents the input vector features, including CP, CB, CC, BP, SP, and MP, while yi represents the output value associated with xi. A linear regression function is established in the high-dimensional feature space:

\( y(x)={W^{T}}Φ(x)+b \)

Where W is the weight vector of the hyperplane, Φ(x) represents the sample data points, and b is the bias term. After initializing a set of particles, they become random particles. During the iterative search process, particles adjust their states based on individual best values and global best values to find the global optimum. The formula for this adjustment is as follows:

\( \begin{cases}{V_{i,n+1}}=ω{V_{i,n}}+{C_{1}}{r_{1}}({p_{i,n}}-{x_{i,n}})+{C_{2}}{r_{2}}({G_{i,n}}-{x_{i,n}})(i=1,2,…,m) \\ {x_{i,n+1}}={x_{i,n}}+{V_{i,n}}\end{cases} \)

The fitness of each particle is calculated using the following formula:

\( S(x)=min(j=1,2,…,J) \)

2.2.2. LightGBM

The LightGBM model has been widely applied in various fields. For instance, Amin et al. used the LightGBM model in the construction industry, while Kim combined LightGBM with XGBoost to build a ship electricity demand forecasting model. Zhong J. utilized the LightGBM model to predict PM2.5 levels at different times of the day. The successful application of the LightGBM model in these fields demonstrates its effectiveness and success.

LightGBM Model Building Process is as follows:

The initialization process begins with the following formula:

\( {f_{0}}(x)={arg_{c}}min\sum _{i=1}^{N}L({y_{i}},c) \)

Negative Gradient Residual of the Loss Function:

\( {{r_{mi}}=-\lbrace \frac{∂L[{y_{i,}}f({x_{i}})]}{∂f({x_{i}})}\rbrace _{f(x)={f_{m-1(x)}}}} \)

Minimization of the Loss Function:

\( {c_{mj=}}{arg_{c}}min \)

Update of Regression Tree:

\( {f_{m}}(x)={f_{m-1}}(x)+\sum _{j=1}^{J}{c_{{mj^{I}}}} \)

After completing the iterations, the final LightGBM model can be expressed as:

\( \sum {f_{M}}(x)=\sum _{m=1}^{M}\sum _{j=1}^{J}{c_{{mj^{I}}}} \)

3. Results

3.1. PSO-SVM Model Prediction

The training ratio was first set to 0.7, and the number of iterations for the Particle Swarm Optimization (PSO) algorithm was set to 1000. Using RMSE (Root Mean Square Error) as the fitness function, the PSO algorithm was employed to search for the optimal cost and gamma parameters for the SVM model. The best RMSE was found to be 0.07844671, with a corresponding cost of 5.3092488 and a gamma of 0.5643647. The performance of the model on the training set is illustrated in Figure 1.

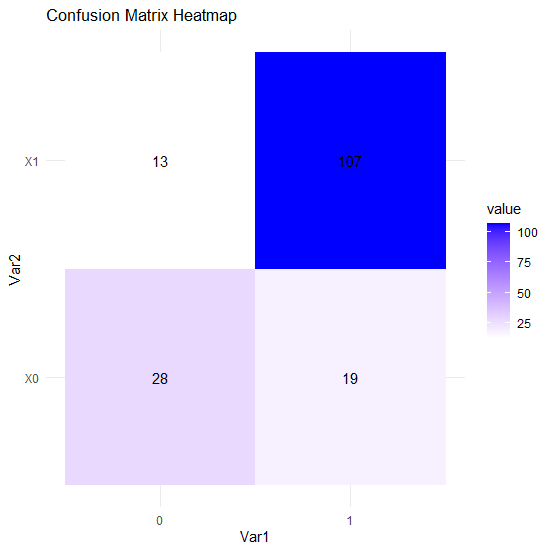
Figure 1. PSO-SVM Model Prediction Performance

3.2. PSO-LightGBM Model Prediction and Feature Extraction

Since the SVM model cannot directly measure the importance of extracted feature variables, the PSO algorithm was used again with RMSE as the fitness function to search for optimal configuration parameters for the LightGBM model. The prediction performance of the model is shown in Table 2.

Table 2. PSO-LightGBM Model Prediction Performance

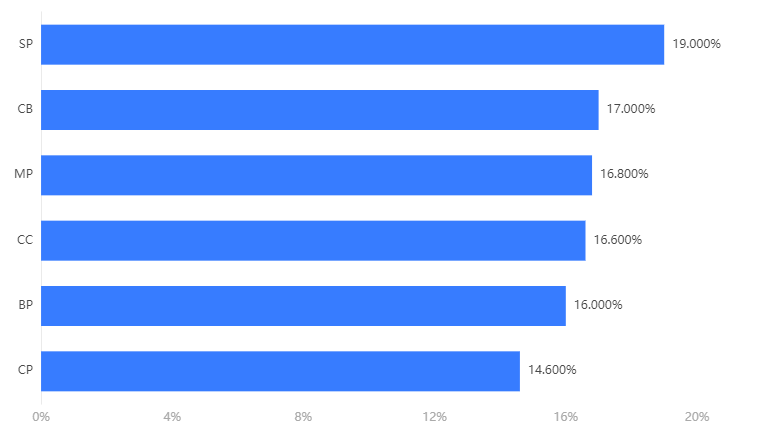
Figure 2. The Importance of Feature Variables in Predicting the Results

The data from Figure 2 indicates the importance ranking of each influencing factor as follows: SP (Personal Privacy), CB (Breach Penalty), MP (Civility), CC (Convenience), BP (Willingness to Pay), and CP (Perceived Transaction Cost). It can be seen that users are most concerned about personal privacy, followed by breach penalties, civility, convenience, willingness to pay, and perceived transaction costs. When designing and implementing the platform in the future, the infrastructure should consider this order when setting platform functionalities to improve adaptability, user acquisition, and usage rates. Privacy should be prioritized as a key focus in development, followed by the design of the breach penalty system. The remaining functional modules should be developed in sequence, with attention to the platform's overall collaborative development.

3.3. PSO Robustness of the PSO Algorithm

To verify the robustness of the PSO algorithm, a similar process was applied using a random forest model to predict feature variables. The prediction results are shown in Table 3, and the feature extraction of the random forest model is illustrated in Figure 3.

Table 3. PSO-Random Forest Model Prediction Performance

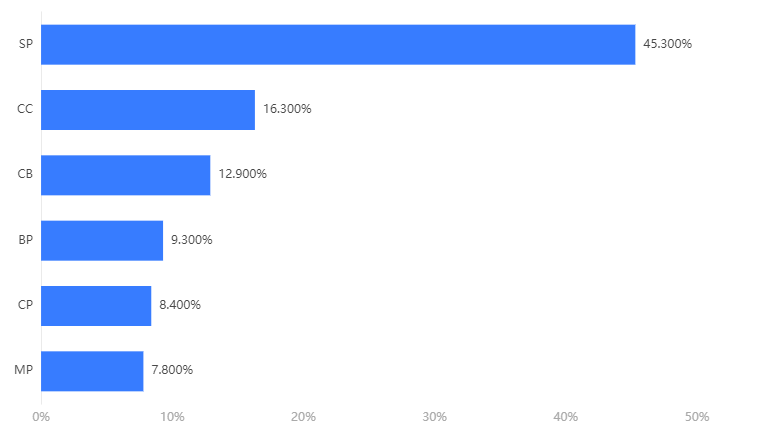
Figure 3. The Feature Extraction for the PSO-Random Forest Model

By using the PSO algorithm for parameter optimization, the random forest model also achieved good prediction performance, with only slight differences in the extraction of key features.

4. Practical Implications

By embedding the PSO algorithm into the various layers of a shared platform architecture, it is possible to achieve accurate predictions of user behavior and market demand while automating the adjustment of machine model parameters. The key elements include high-quality data collection and processing, effective algorithm integration and optimization, real-time decision support, and continuous feedback and improvement. Following these steps can enhance the platform's intelligence, optimize resource allocation, and improve user experience.

4.1. Data Collection and Preprocessing Layer

The first step is to collect and process data related to user behavior and market demand for subsequent analysis and optimization. First, collect data from multiple sources, such as user interaction records, market transaction data, and sensor data, ensuring that the data is comprehensive and has a sufficient sample size. Second, handle missing values, outliers, and noise to ensure data quality. Third, Standardize and normalize the data, perform feature engineering (e.g., feature selection, feature extraction), to enhance the model's accuracy.

4.2. Algorithm Integration and Optimization Layer

The goal of this layer is to integrate the PSO algorithm into the shared platform and optimize its parameters to improve prediction and scheduling performance. The first step is to define the PSO algorithm’s objective function. For example, the objective function for user behavior prediction could be minimizing prediction error, while market demand prediction could aim to maximize forecast accuracy. Set the parameters for the PSO algorithm, including the number of particles, iterations, and learning factors. The second step is to use the processed data to train predictive models (e.g., regression models, time-series models). Employ the PSO algorithm to optimize model parameters, such as tuning hyperparameters to improve prediction accuracy. The PSO algorithm continuously updates model parameters and iterates until the predefined optimization goal is reached. Last, once optimized, integrate the PSO algorithm into the platform’s computational framework to ensure that it can run in real-time or on a scheduled basis to update model parameters continuously.

4.3. Decision Support and Service Layer

The purpose of this layer is to utilize the optimized model for predictions and to provide decision support services. First, use the optimized model to predict user behavior, market demand, etc. Generate prediction reports or real-time dashboards displaying data. And provide decision support functionalities, such as recommendation systems or demand forecasting analyses. Based on prediction results, automatically adjust machine parameters or resource allocation strategies. Implement an automated scheduling system that transforms the predictions into actionable operational instructions.

4.4. Feedback and Optimization Layer

The Feedback and Optimization Layer is designed to monitor the results of predictions and scheduling while continuously optimizing the algorithm and model. First, collect real performance data from the predictions and scheduling outcomes, and evaluate their effectiveness. Periodically gather user feedback and market responses to assess the real-world impact of the predictions and scheduling. The second step is model adjustment. Based on actual performance and feedback, adjust the parameters of the PSO algorithm and the model structure. This may involve reprocessing data and retraining models. Iteratively optimize the PSO algorithm to further improve prediction accuracy and scheduling efficiency. The last step is continuous improvement. Regularly evaluate the performance of the model and optimize the algorithm to adapt to changing market conditions and user behavior.

A system architecture diagram based on the above design is shown in Figure 4:

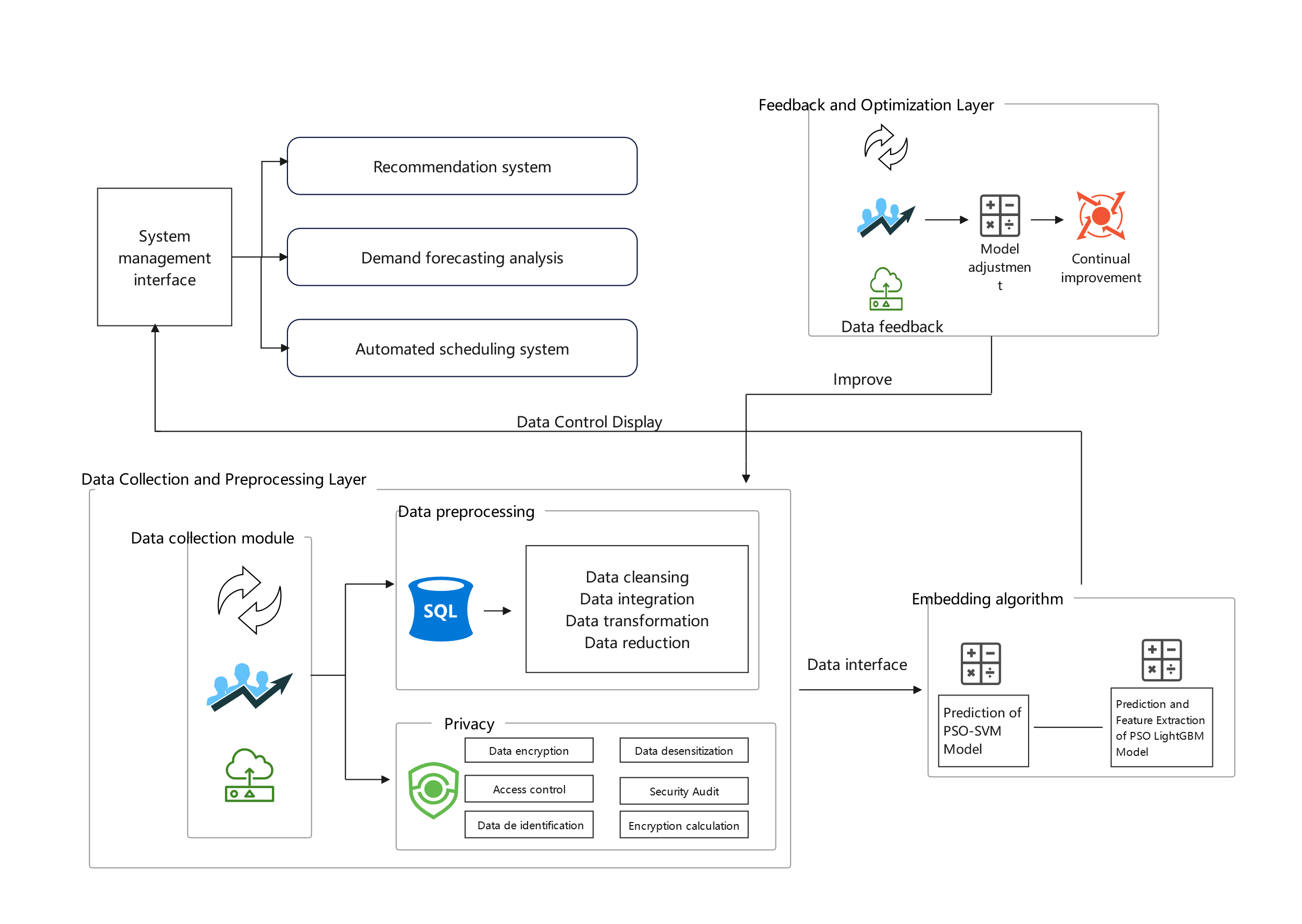
Figure 4. System Architecture Diagram

5. Conclusion

The use of the PSO algorithm significantly accelerates the training speed of machine learning models by improving the speed of parameter optimization, allowing the optimal parameter combination to be quickly identified. Since the performance of machine learning models heavily depends on parameter selection, traditional methods such as grid search and random search, while straightforward, tend to be inefficient. When faced with a large parameter space, the PSO algorithm, by simulating bird flock foraging behavior and utilizing information sharing and collaboration between particles, can more rapidly find the optimal parameter combination, thus speeding up the training process and significantly reducing training time. In addition to accelerating the training process, PSO improves model performance by enhancing both accuracy and generalization capability. The application of the PSO algorithm also greatly saves computational resources, which is especially important for embedded systems or mobile devices, optimizing energy usage efficiency. For large-scale data analysis and computational systems, this means a substantial reduction in energy consumption and operational costs. The algorithm's flexibility and broad applicability also improve when embedded in such systems. Since the SVM model cannot perform feature extraction, the LightGBM model was introduced to handle feature extraction. LightGBM, a highly efficient gradient boosting framework, helps reduce memory consumption, enabling the system platform to operate with high efficiency and low memory usage.

However, the PSO algorithm has limitations, such as a tendency to fall into local optima rather than finding the global optimum, which can affect final decision-making outcomes. Additionally, the sensitivity of parameter tuning can increase the difficulty of integrating the algorithm into the platform and, as the data volume increases, it may lead to increased computational complexity, affecting the platform’s real-time capabilities and response speed. These challenges highlight key areas for future research and improvement.