1. Introduction

Those who are familiar with World War II history may know that the Enigma was an intelligence-encryption device used by Nazi Germany. It was a cryptographic machine used to encrypt and decrypt documents in order to prevent the Allies from deciphering secret German information. The essence of the Enigma machine algorithm is a symmetric encryption algorithm [1]. That is, after the user enters the information into the machine or system, a ciphertext can be obtained. Also, the original information can be obtained by reverse operation of the ciphertext. In a real application, in order for a message to be encrypted and decrypted correctly, the settings of the Enigma machine that sends and receives the message must be the same; The rotors must be exactly the same, and they must be arranged in the same order, starting positions and connections to the strips. All of these settings need to be determined before use and recorded in the password book. Since the Enigma machine has so many impressive functions in the field of cryptography, this paper will explore the specific working principle of the Enigma machine and its internal structure. The security of the Enigma machine will be proved by mathematical proof. In addition, based on this, the application of the Enigma machine in daily life will be probed further, such as the mathematical principle of using code to simulate the work of the Enigma machine and the internal series network of making a simple Enigma machine to dynamically restore its work.

Figure 1. Enigma machines were used to send messages in World War II [2].

2. Structure and mathematical principle of the enigma machine

The common the Enigma machine is mainly composed of five parts, which are plugboard, rotors, keyboard, lamp board and reflectors.

Figure 2. Plugboard [3]. Figure 3. Keyboard and Lamp board[4].

Figure 4. Rotors[5]. Figure 5. Reflector[5].

The outermost structures are keyboard and lamp board, which generally have 26 letters. Unlike keyboard, the letters on the lamp board can be lit. Every time you press the letter on the keyboard, the letter on the lamp board lights up. If you type ciphertext on the keyboard then the lit letters are in plain text. Generally speaking, there are only three rotors in the Enigma machine, and each rotor has 26 numbers corresponding to 26 letters. Each rotor is connected by electrically conductive metal rods to transmit a current signal. Inside each rotor, several wires are scrambled to ensure that every signal sent out is irregular. When the signal passes through the three rotors, it arrives at the reflector. Like the rotor, the reflector has 26 metal rods attached to the rotor and a lot of irregularly connected wires.

The current signal arrives at the reflector, then enters the leftmost rotor, and finally leaves the rightmost rotor. At the same time, each rotor can rotate in a different position, making it difficult to predict which letter will come out of and where it enters. When the electrical signal comes out of the right-most rotor, it will reach the front plugboard. There are many slots on the plugboard, and you can swap two letters by pulling or installing the plug. Suppose you want to switch the letters ‘A’ and ‘D’, all you had to do was plug into the slot ‘A’ and slot ‘D’, and a connected circuit would form. By doing so, the final result is further encrypted, which also, of course, greatly improves security.

Figure 6. Insert the plug into the slot where you want to convert letters [6].

However, why is the Enigma machine so secure? As mentioned above, each part of the Enigma machine has many different combinations.

In plugboards, we assume that there are cables connected to the plugboard. ( \( 0≤p≤13 \) ), so, we get the total possible different combinations of sockets are \( C_{2p}^{26} \) .

Since each time you plug in the cable, the corresponding socket decreases by one so we can get the connection mode between cables and sockets as:

\( (2p-1)(2p-3)(2p-5)…(3)(1)=(2p-1)‼ \) (1)

Hence, the number of different connections that have been made by an Enigma machine is:

\( C_{2p}^{26}×(2p-1)‼=\frac{26!}{(26-2p)!×p!×{2^{p}}} \) (2)

Therefore, we get the total number of board combinations is:

\( Σ_{p=0}^{13}\frac{26!}{(26-2p)!×p!×{2^{p}}}=532,985,208,200,576 \) (3)

Which is a very huge number

For the three ordered rotors, theoretically, there should be combinations of discs that can be built independently. This is because the disc in the middle of the rotor communicates input points and output points on both sides. However, considering that rotor rotation correction is required in every encoding or decoding process, you can select one of the discs from possibilities of leftmost, also, you can select one of them from of middle and one of them from of rightmost [5].

Hence, the number of all possible combinations is:

\( 26!×(26!-1)×(26!-2) \) (4)

The third variable is the initial rotation position of the three rotors, because each rotor corresponds to letters, so the total number of different initial positions is \( {26^{3}} \) .

In addition, the movable ring on each rotor contains a notch. When the user encodes with an Enigma machine, the rightmost rotor rotates every time. Similar to the decimal mathematical calculation of one in ten. The gap in the right-most rotor causes the middle rotor to rotate once after each rotation cycle (usually 26 times from a certain letter). Similarly, when the middle rotor completes its rotation cycle, its notch forces the leftmost rotor to rotate every strokes of the key. Since the leftmost rotor is the last rotor, all possible combinations are \( {26^{2}}=676 \) [5].

The last variable is the reflector. Like the rotor, the reflector has 26 points of contact, but only one connecting surface. On one of the surfaces of the reflector. Unlike the rotor. The reflector is designed with wires connected internally to points of contact, so that electrical signals from the leftmost rotor enter the reflector and return through the rotor, but through different points of contact.

Similar to the position of the plug selected for the plugboard, when the first wire is connected to a random contact, there are 25 different connections at the other end. When the second wire is connected in the same way as the first wire. There are 23 different connections. And so on, when all the contacts have been connected, we can get the total number of different connections for the reflector:

\( 25‼=\frac{26!}{(13!×{2^{13}})}=7,905,853,580,625 \) (5)

Which is also a huge number.

It is obvious that every part of the Enigma machine can produce an unimaginable number of different combinations. Under the conditions of the time, it was difficult to decipher the Enigma machine with human hands or even machines.

3. Expansion

The research split this part into two parts, the first is the code presentation and the second is the self-made the Enigma machine.

In the code display section, the research tried to implement some of the most basic functions of the Enigma machine. Strip out keyboard and lamp board for input and output, and the code represents the rest of the working logic.

In “Plugboard” part, the research wants to randomly generate numbers that correspond to 26 letters between 0 and 25. Because a plug swaps two letters at the same time, the research wants to be able to extract two numbers at the same time for pairing. The role of the for loop is to match the first two digits in the scrambled number. The next step is a simple ASSII code conversion. The reflector section does this using a simple superclass extension.

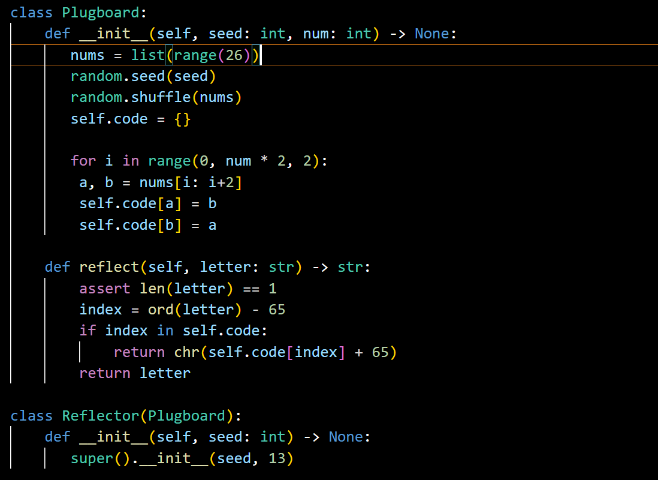
Figure 7. Plugboard code.

The next focus is on the “Rotor”. The previous part, like plugboard, needs to introduce and generate random numbers. At this point, two functions ‘forward’ and ‘backward’ are introduced, representing forward and reverse passing through the rotor respectively. Then the research added a ‘step’ function to determine whether the rotor needed to carry or not, and when it completed 26 turns, the Boolean value was ‘True’ to advance one, and vice versa.

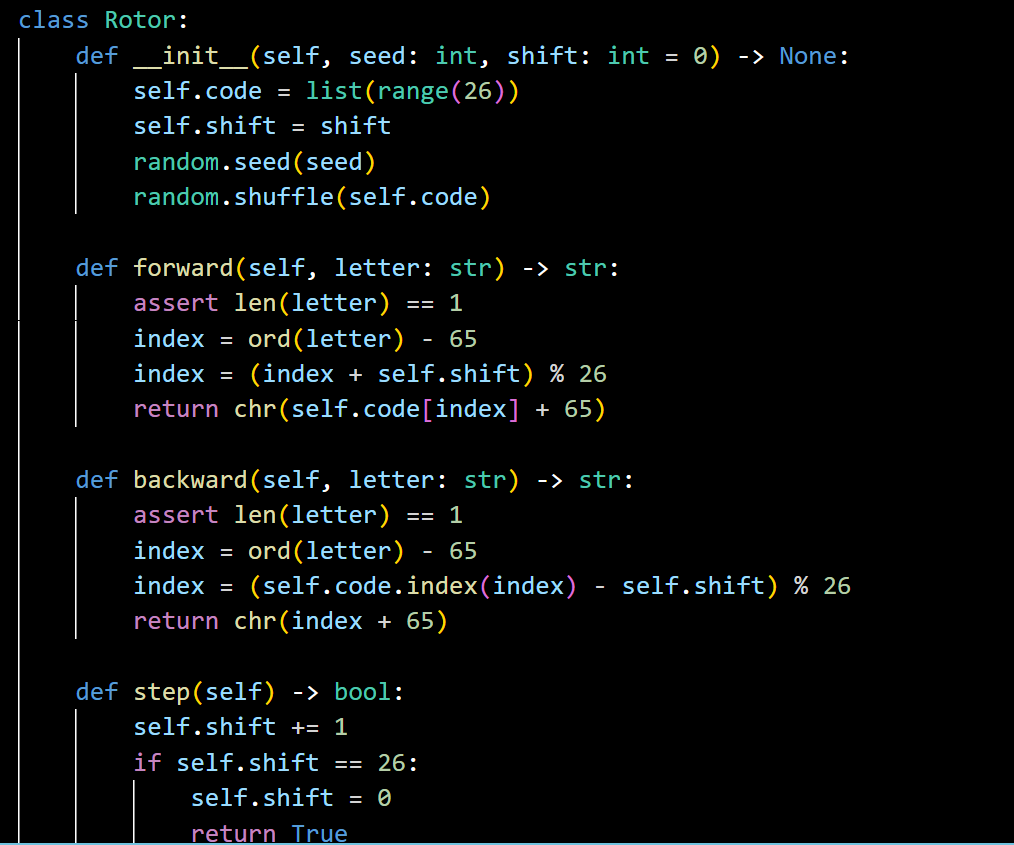
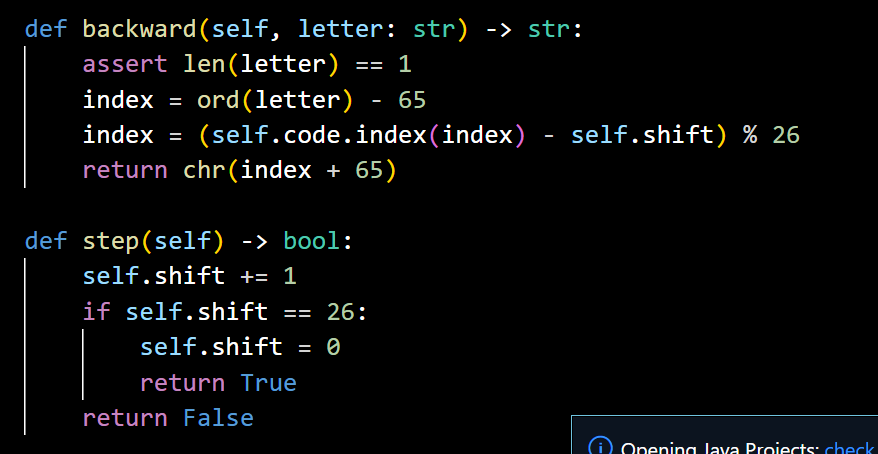
Figure 8. Rotor code.

The research ended up creating a class called "Enigma". The ‘process’ function represents the process of decoding or encoding. Of course, the "process" function alone is not enough. The research also needs a ‘process_appendix’ function to get more stuff passed in each time, instead of typing it again and again. Finally, "step" each time press a key. It is using a variable called "carry" to see if it's running.

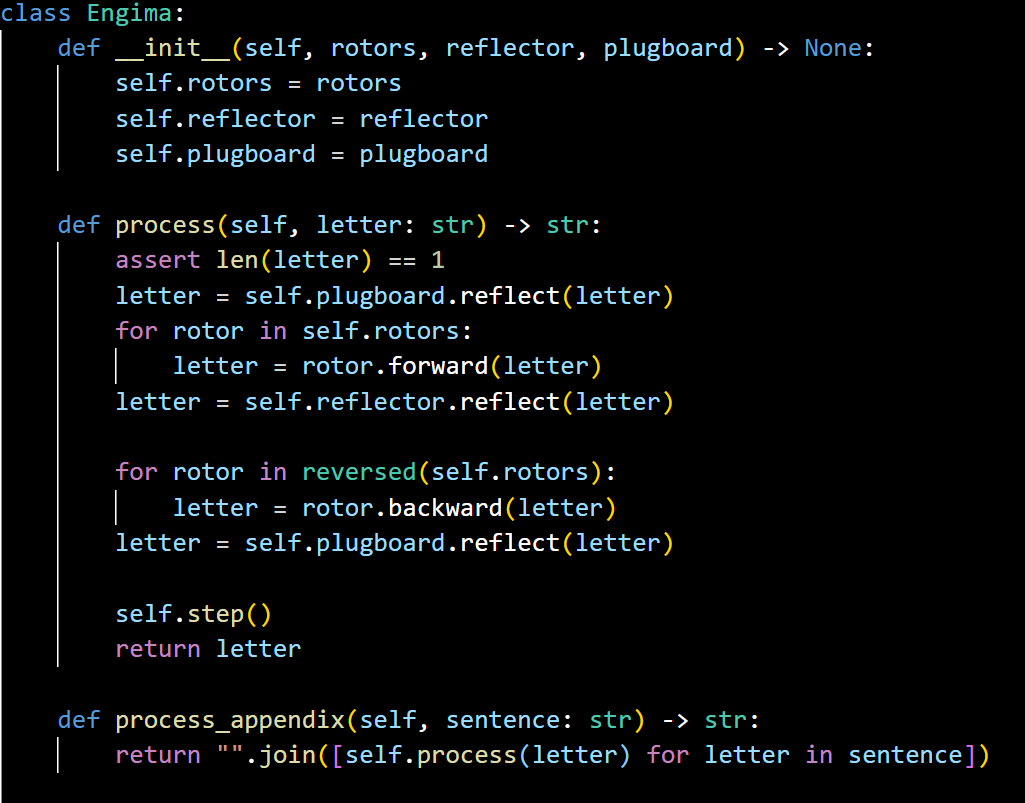
Figure 9. Enigma code.

Testing the code:

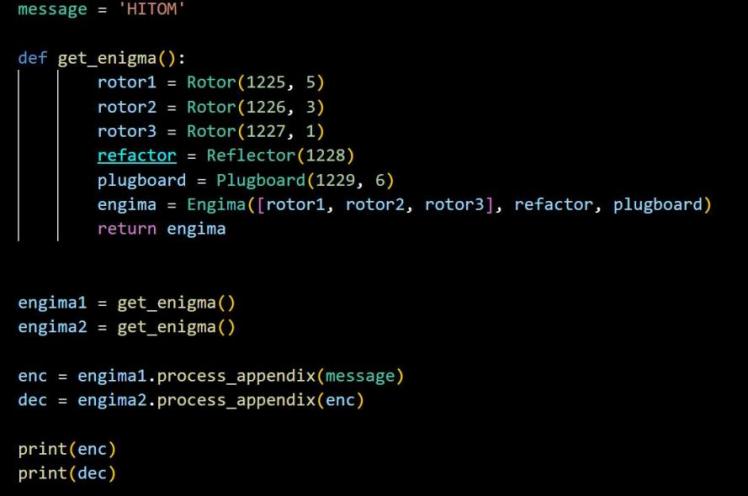
Figure 10. Testing part.

After testing, the code works!

This part is about how a self-made Enigma machine work:

Figure 11. Self-made enigma machine test.

Figure 12. Self-made enigma machine test. Figure 13. Self-made enigma machine test.

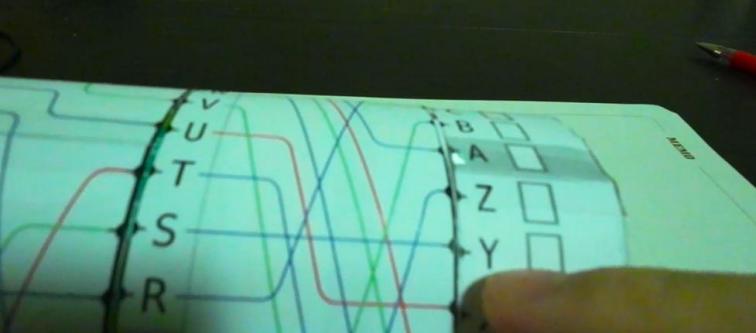
Figure 14. Self-made enigma machine test. Figure 15. Self-made enigma machine test.

Figure 16. Self-made enigma machine test.

4. Conclusion

In conclusion, the Enigma machine as one of the greatest coding machines of the last century has indeed greatly influenced the future development of cryptography. The mechanical components and circuit components are used to change the input electrical signal to different degrees. Physically, the same input has tens of thousands of different possibilities of output under the coordination and change of different components. This was a remarkable innovation in the evolution of cryptography, and it led to the renewal and acceleration of cryptographic methods.

In this paper, the re-exploration of the structure of the Enigma machine is the integration and induction of the principle of the Enigma machine based on predecessors. From a popular point of view explain the Enigma machine in the physical encryption process and working mode. Since every structure has more or less movable components and different combinations. Therefore, taking this as an opportunity, this paper continues to deeply explore its internal mathematical principles, in a more intuitive way to explain the security of Enigma machine. Of course, what is described in this paper is only to discuss the possibility of different combinations of existing components of Enigma machine, because of the problem of equipment and funds. It has not been discussed in a more in-depth way, which is worthy of attention in the subsequent research.

A wonderful part of this paper is that it has made a basic and valuable restoration for the practical application of Enigma machine in life. Using the code to reveal the working principle of the Enigma machine, and can carry out some simple encryption and decryption. A simple Enigma machine was made with the materials around, and a decoding process was successfully completed with it. These are the most remarkable points in this study. However, the study of Enigma machine does not end there. In the next stage of research, we will summarize the shortcomings of this experiment and the areas that can be improved, and further explore the problems that have not been involved in this project.