1. Introduction

Dark matter is hypothesized to make up approximately 27% of the universe’s total mass-energy content and plays a crucial role in the formation and structure of galaxies due to its gravitational influence. The concept was first proposed to explain discrepancies between observed and expected motions of galaxies. Over time, multiple lines of evidence have reinforced the need for dark matter, leading to its acceptance as a fundamental component of modern cosmology.

One of the earliest hints of dark matter came from Swiss astronomer Fritz Zwicky in the 1930s. While studying the Coma Cluster, he noticed that the galaxies within the cluster were moving much faster than expected based on the visible mass. He hypothesized the existence of “dunkle materie” (dark matter) to explain the additional gravitational pull required to keep the cluster intact [1]. Since then, dark matter has been supported by numerous astronomical observations, including gravitational lensing and galactic rotation curves.

2. Gravitational Lensing as Evidence for Dark Matter

Gravitational lensing occurs when light from a distant object, such as a galaxy or quasar, bends around a massive foreground object due to gravity. This phenomenon, predicted by Einstein’s General Theory of Relativity, provides direct evidence for unseen mass in the universe. The bending of light allows astronomers to measure the total mass of galaxy clusters, often revealing a discrepancy between visible mass and gravitational effects.

Studies of gravitational lensing show that the total mass responsible for bending light far exceeds what is observable in terms of stars and gas [2]. This excess mass is attributed to dark matter, forming halos around galaxies and clusters. The Bullet Cluster, a well-known case, provides some of the strongest evidence for dark matter, as its gravitational lensing maps clearly separate visible mass from an unseen, dominant mass component [3].

In a typical spiral galaxy, stars and materials closer to the galactic center rotate at higher speeds due to stronger gravitational forces. On the other hand, materials farther from the center are expected to rotate more slowly. However, observations have shown that even in regions far from the galactic center, the rotational speed remains nearly constant. This phenomenon cannot be explained by the mass distribution of visible matter alone, leading scientists to propose the existence of dark matter to account for this anomalous rotational pattern.

3. Gravitational Lensing Effect

The key evidence supporting dark matter comes from galactic rotation curves, which plot the rotational velocity of stars as a function of their distance from the galactic center. According to Newtonian mechanics, objects farther from the center of mass should rotate more slowly, similar to planets in the Solar System. However, observations of spiral galaxies, particularly those by Vera Rubin and Kent Ford in the 1970s, revealed that outer stars move at nearly the same speed as inner ones [4]. This discrepancy suggests that galaxies contain much more mass than what is visible.

The only viable explanation for these flat rotation curves is the presence of a large, unseen mass component, or dark matter, that extends beyond the visible galaxy. Without dark matter, galaxies would not have enough gravitational pull to keep their outer stars from flying apart, indicating that dark matter plays a vital role in galactic structure and stability.

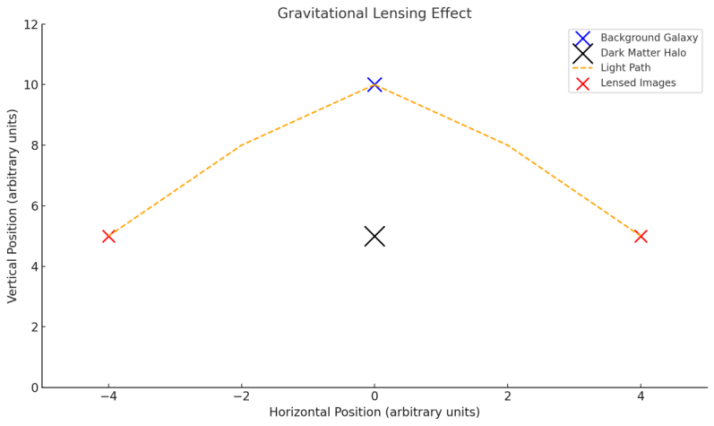
Figure 1: Gravitational Lensing Effect

Figure 2: Source and Lens Planes [5]

In Figure 1, the background galaxy (blue point) emits light that passes near a massive object (black point representing a dark matter halo). The light is bent by the object's gravitational field, forming lensed images (red points). The orange dashed lines show the distorted light paths, illustrating how gravitational lensing works.

The simplest model is the deflection of light passing through a mass object, as shown in Figure 2. In this case, assuming that the aiming distance of the photon is b and the mass of the object is M, the transverse acceleration of the photon is obtained by Newtonian mechanics:

\( {g_{⊥}}=\frac{GMb}{{({b^{2}}+{z^{2}})^{3/2}}} \) (1)

The speed of the transverse direction is:

\( {v_{⊥}}=∫{g_{⊥}}dt=\frac{2GM}{bc} \) (2)

So the deflection angle of the light is:

\( α=\frac{{v_{⊥}}}{c}=\frac{2GM}{b{c^{2}}} \) (3)

Except that the light rays are close to the Schwarzschild radius, the gravitational force corresponding to the general gravitational lens is very weak, so GMm/r<<mc2, the weak field condition is valid. So it can be approximated by Newton's theory. The above derivation is carried out under the condition of weak field approximation. It is worth mentioning that the weak field approximation does not imply a weak lens. For strong lenses, the weak field approximation is also valid, since GMm/r<<mc2 is also true at locations far from the Schwarzschild radius.

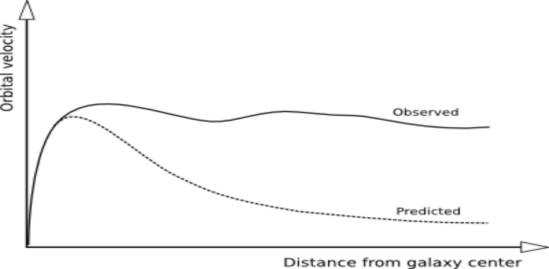
Figure 3: Galactic rotation curves

Figure 4: Observed Rotation Curve [6]

Figure 3 shows rotation curves of the spiral galaxy NGC 3198 measured by the THINGS collaboration. The observed rotational curve \( vobs(r) \) is of contributions from baryons \( vb(r) \) (stars in the disk and bulge, and gas), and also from the halo of dark matter \( vh(r) \) .

Figure 4 shows the expected rotation speed of stars, which declines with distance based on visible matter, The dashed line represents the observed rotation speed, which remains flat, indicating the presence of dark matter. Based on Newton’s theory of gravitation, \( v=\sqrt[]{(GM/r)} \) . By definition, we know: \( dv={a^{*}}dt \) .

The upper figure of Figure 4 demonstrates the change in velocity v of uniform circular motion \( dv=ω*dt \) , in which omega is angular speed. It mainly depends on changing its direction of motion, \( ω=\frac{dθ}{dt} \) . The downside figure of Figure 4 shows the main source of acceleration a is gravity, i.e., \( g=\frac{GM}{{R^{2}}} \) , where G is the gravitational constant and M is the gravitational mass. So, it can be concluded that \( v*ω*dt \) = \( \frac{GM}{{R^{2}}} \) .

With all that ground information and the observations that The arms of a spiral galaxy revolve around the center of the Milky Way. The luminous mass density of spiral galaxies decreases as they move from the center to the periphery. If the luminous mass is all matter, then we can model the galaxy as the point mass at its center and test the mass orbiting it, similar to the solar system. According to Kepler's third law, the rotation speed is expected to be similar to that of the solar system, decreasing as the distance from the center increases. This has not been observed. In contrast, the galactic rotation curve remains flat as the distance from the center increases. If Kepler's law is correct, then the obvious way to resolve this discrepancy is to conclude that the mass distribution in spiral galaxies is not similar to the mass distribution in the solar system. In particular, there is a large amount of non-luminous matter (dark matter) in the outer reaches of galaxies.

4. Galaxy Clusters

Galaxy clusters are particularly important for dark matter research because their masses can be estimated in three independent ways: from the dispersion of the radial velocities of galaxies within the cluster. The X-ray emission from the hot gas in the cluster, based on the X-ray spectrum and flux, can estimate the gas temperature and density, and thus give the pressure; It is assumed that the pressure and gravity balance determine the mass distribution of the cluster. Gravitational lensing (usually of more distant galaxies) can measure the cluster mass without relying on kinetic observations (such as velocity). In general, the three methods reasonably agree that dark matter outweighs visible matter by about 5 to 1.

To make the observed rotation curves consistent with gravitational theory, scientists propose that galaxies must be surrounded by dark matter halos. These dark matter halos extend far beyond the visible boundaries of galaxies, and their mass far exceeds that of visible matter. When the mass of dark matter is incorporated into the calculations, the observed flat rotation curves can be accurately explained.

The existence of dark matter can also maintain the stability of spiral galaxies and prevent them from disintegrating due to high-speed rotation. Research shows that the amount of dark matter in a galaxy is approximately five times that of visible matter, which means that the vast majority of the mass in a galaxy is not stars or gas, but dark matter.

5. Alternative Theories and Their Challenges

Although the dark matter theory is the most widely accepted explanation, there are still some alternative theories, such as Modified Newtonian Dynamics (MOND). This theory suggests that gravity may exhibit different laws on cosmic scales. However, MOND has difficulties in explaining the cosmic microwave background radiation and gravitational lensing phenomena, while the dark matter model can explain these phenomena well.

In addition to rotation curves, velocity dispersion studies provide further support for dark matter. In gravitationally bound systems, such as elliptical galaxies and globular clusters, stars must obey the Virial theorem, which relates their velocities to the total gravitational mass of the system. However, observed velocity distributions often exceed what is expected from visible matter alone [7].

For instance, measurements of elliptical galaxies show higher-than-expected velocity dispersions, implying the presence of additional unseen mass. Similarly, X-ray observations of galaxy clusters reveal that the hot intracluster gas moves too fast to be bound by the visible matter alone, further suggesting the dominance of dark matter in these structures [8].

6. Conclusion

The study of dark matter remains one of the most intriguing challenges in contemporary astrophysics. Observational evidence from gravitational lensing, galactic rotation curves, velocity dispersion, and galaxy cluster dynamics strongly supports its existence. This paper has certain shortcoming, such as the lack of experiment and data analysis. In the future, the author will try to investigate deeper in this field through personal observation and data collection.

Although alternative theories exist, none have provided a comprehensive explanation that rivals the dark matter model. Future advancements in detection methods and theoretical models may finally unveil the true nature of this mysterious substance, shaping people’s understanding of the universe.