1. Introduction

With the rapid development of economy, people's requirements for the quality of life are increasing day by day. In the field of electrical equipment, air conditioning and other environmental regulation devices are gradually popular. Air conditioning achieves indoor air circulation by absorbing or releasing heat from the surrounding air, so as to achieve the purpose of regulating temperature. However, while regulating temperature, air conditioning may also cause a series of problems such as dry indoor air and decreased air quality. Therefore, the best way to solve the above problems is to optimize the overall design of air conditioning according to the shape of the room, and to deeply study the influence of the location, number, wind direction, Angle, wind speed and air volume of air conditioning on temperature change[1].

2. Establishment and solution of optimization model of air inlet and outlet shape

For an approximately rectangular room, the size is 5m×8m×3m, equipped with an air conditioner, the maximum volume is 0.1m ³, the rated power is 1800W, the maximum wind speed is 8.0m /s, and the maximum air flow is 600m ³/h. This paper simulates the change of indoor temperature with time and space in different seasons, establishes an optimization model, and determines the best shape and size of air conditioning.

2.1. Establishment of the Equation for Air Circulation

The air flow is a compressible Newtonian fluid, so the Navier-Stokes equation [2] is established here to describe the air flow. Its essence is momentum conservation, which can be expressed as follows:

\( ρ(\frac{∂u}{∂t}+u\sqrt[]{V}u)=-∇p+∇[(μ(∇u+(∇u{)^{T}})-\frac{2}{3}μ(∇[u])I)+F \) (1)

Where, u is the air flow velocity, p is the air pressure, p is the air density, \( μ \) is the aerodynamic viscosity. This equation is solved simultaneously with the continuity equation, which is the conservation of mass, and is expressed as follows:

\( \frac{∂ρ}{∂t}+∇[(ρu)=0 \) (2)

In order to relate the Navier - Stokes equations to temperature, heat is introduced based on \( Q=νRΔT \) [3]. For any object, the law of conservation of energy is satisfied. Taking the length and width of the room as the base, a three - dimensional rectangular coordinate system is established. Taking the micro - element in the given fixed - volume room, it satisfies \( {Q_{inf}}+{Q_{s}}={Q_{T}} \) , where \( {Q_{inf}} \) is the inflow heat, \( {Q_{s}} \) is the heat from the heat source, and \( {Q_{T}} \) is the heat that raises the temperature. Considering that \( \vec{Q}=-kΔu \) is deduced from Fourier's law of heat conduction, substituting it into the heat conservation, the heat conduction equation is derived:

\( \frac{∂u}{∂t}={α^{2}}Δu+F(t,\vec{x}) \) (3)

Where, \( α=\sqrt[]{\frac{κ}{cρ}} \) , \( F(t,\vec{x})=\frac{g(t,\vec{x})}{cρ} \) . Substituting into (3), the heat - transfer equation can be simplified as:

\( \frac{∂u}{∂t}=\frac{κ}{cρ}Δu+\frac{g(t,\vec{x})}{cρ}=\frac{1}{cρ}(κΔu+g(t,\vec{x})) \) (4)

Where, k is the thermal diffusivity coefficient, \( g(x,y,z,t) \) represents the heat - generation rate of the internal heat source per unit volume, and c is the specific heat capacity of air. Finally, by combining (1), (2) and (4), the equation that can describe the air flow and temperature change is obtained:

\( ρc\frac{∂T}{∂t}+ρ◻c◻(\vec{u}∇T)=κ{∇^{2}}T+{Q_{s}} \) (5)

2.2. Establishment of optimization model for high-performance air conditioning

2.2.1. Objective function

The optimization of air conditioning performance is carried out from three aspects, one is temperature uniformity, the other is energy efficiency, and the last one is the high control of noise[4].

The first objective is temperature uniformity. The temperature distribution of high-performance air conditioning in the temperature field should tend to be uniform, so the first objective can be expressed as follows:

\( Tempretur{e_{u}}niformity=\frac{1}{V}∫{|T(x,y,z)-{T_{target}}|^{2}}dV \) (6)

Where, \( T(x,y,z) \) represents the temperature of each coordinate in the temperature field [5] of the three-dimensional coordinate system of the room established based on the air circulation model, and \( {T_{target}} \) represents the target temperature set by the user for the air conditioner. Air conditioning temperature uniformity is represented by the sum of temperature differences in the temperature field of the whole room.

The second goal is the highest energy efficiency. The energy efficiency of air-conditioning cooling and heating can be expressed by the ratio of cooling energy efficiency to that of heating energy efficiency. Here, it can be summarized as efficiency:

\( η=\frac{{Q_{s}}/Δt}{P} \) (7)

\( {Q_{s}} \) is the heat source heat, refrigeration is the cooling capacity, and heating is the heat, \( Δt \) is the heat source action time, P is the electric power of air conditioning.

The third objective is noise high controllability. There is a positive correlation between wind speed and noise, and the appearance of air conditioning also affects its noise. Considering that the air conditioner designed in this paper is improved based on the existing air conditioners on the market, only the influence of wind speed is considered at this time. To simplify the model, a noise function is constructed and a coefficient is set based on this function, which is expressed as:

\( noise=δu+ε \) (8)

Taking the above three characteristics as the objective function, a multi-objective programming model is constructed. In order to simplify the calculation difficulty of the model, the utility function of air conditioning is constructed here, and the multi-objective programming is transformed into a single objective programming model.

The utility function of air conditioning is expressed as follows.

\( utility={α_{1}}η-{α_{2}}Tempretur{e_{u}}niformity-{α_{3}}noise \) (9)

Where, \( {α_{1}} \) , \( {α_{2}} \) and \( {α_{3}} \) are their weighting coefficients, which reflect the priority of the three indicators.

2.2.2. Constraints

Suppose the volume of air conditioning is \( {V_{a}} \) , if is a cuboid, its length, width and height are a, b, c, then \( {V_{a}}=abc \) ; If is a cylinder, then the diameter is d, then \( {V_{a}}=\frac{1}{4}π{d^{2}}c \) , the maximum volume of the air conditioning is known to be 0.1 cubic meters, and can be expressed as follows:

\( {V_{a}}≤0.1 \) (10)

The power should be less than the rated power, and the wind speed should be less than the maximum wind speed, which is expressed as follows.

\( P≤{P_{e}}=1800 \) (11)

The wind speed should be less than the maximum wind speed:

\( u≤8 \) (12)

Based on \( c=\frac{{Q_{inf}}}{mΔT}=\frac{{Q_{inf}}}{ρ{V_{t}}ΔT} \) , where \( {V_{t}} \) is the air volume per unit tuyere, assuming that the size of each tuyere is equal, the number of seals is n, and the maximum import and export flow is 600 cubic meters, which can be expressed as:

\( n{V_{t}}=\frac{{Q_{inf}}}{cρΔT}≤600 \) (13)

In summary, when designing the shape and size of the air conditioner, only changing the size and shape of the air conditioner, it is taken \( {V_{a}} \) as the decision variable. In the design of the inlet and outlet, the wind speed u, the air volume of the inlet and outlet per unit tuyere \( {V_{t}} \) , and the number of tuyere will be n, and the single objective programming model will be sorted out as follows:

\( \begin{array}{c} min(-utilitg) \\ \begin{cases}\begin{matrix}{V_{a}}≤0.1 & \\ P≤1800 & \\ u≤8 & \\ n{V_{t}}≤\frac{{Q_{eff}}}{cρΔT}≤0.6 & \\ η=\frac{{Q_{t}}/Δt}{P} & \\ utility={α_{t}}η-{α_{2}}Tempretur{e_{w}}aiformity-{α_{3}}xoise & \\ noise=δu+ε & \\ Tempreaw{e_{w}}aigformis)=\frac{1}{V}∫{|T(x,y,z)-{T_{inger}}|^{2}}dV & \\ ρc\frac{∂T}{∂t}+ρ[±(\overset{¯}{u}[NT)=k{∇^{2}}T+{Q_{z}} & \\ {Q_{inf}}+{Q_{z}}={Q_{T}} & \\ \end{matrix}\end{cases} \end{array} \) (14)

2.2.3. Solving the model

The random search algorithm is used to solve the above goal programming model, and finally the best parameter combination that makes the objective function reach the minimum or maximum value is found. Since the model contains differential equations, this paper uses the finite difference method [6][7] to optimize the model on the basis of differential equations.

For a one-dimensional problem, suppose we have a function f(x) with respect to x and apply Taylor expansion:

\( f(x+Δx)=f(x)+\frac{Δx}{1!}\frac{抖f}{抖x}+\frac{Δ{x^{2}}}{2!}\frac{{^{2}}f}{{x^{2}}}+O(Δ{x^{3}}) \) (15)

Ignoring the first derivative of the remainder can be expressed as follows.

\( \frac{?f}{∥x}∥\frac{f(xΔx)-f(x)}{Δx} \) (16)

The scheme, called Euler forward difference, has first-order accuracy due to the first-order function of the neglected term \( Δx \) , which is expected to be a truncation error[8].

Similarly, Euler's backward difference is:

\( \frac{?f}{∥x}∥\frac{f(x)f(x+Δx)}{Δx} \) (17)

Euler backward difference also has first-order accuracy. In order to construct second-order accuracy, firstly, the above two sets of equations are expanded by Taylor company:

\( \frac{1}{1}f(x+Δx)=f(x)+\frac{Δx}{1!}\frac{抖f}{抖x}+\frac{Δ{x^{2}}}{2!}\frac{{^{2}}f}{{x^{2}}}+\frac{Δ{x^{3}}}{3!}\frac{{?^{3}}f}{?{x^{3}}}+O(Δ{x^{4}}) \)

\( \frac{1}{1}f(x-Δx)=f(x)-\frac{Δx}{1!}\frac{抖f}{排x}+\frac{Δ{x^{2}}}{2!}\frac{{^{2}}f}{{x^{2}}}-\frac{Δ{x^{3}}}{3!}\frac{{?^{3}}f}{?{x^{3}}}+O(Δ{x^{4}}) \) (18)

Subtracting the two equations and ignoring the remainder, we get:

\( \frac{?f}{∥x}≫\frac{f(x Δx)-f(x-Δx)}{2Δx} \) (19)

The above equation is the central difference scheme with second-order accuracy.

2.2.4. Seasonal simulation

In order to further simulate the air conditioning gas and fluid process in summer and winter, Lagrangian CFD [9] is used to describe the fluid motion state in this paper. Lagrangian method focuses on the study of the movement of each fluid particle, describes the movement process of the fluid particle from beginning to end and the change law of physical quantities with time t.

\( ?(\frac{抖}{抖x},-\frac{抖}{y},\frac{抖}{抖z})=\frac{}{x}i+\frac{抖}{抖y}j+\frac{}{z}k \) (20)

Velocity gradient:

\( ?V(\frac{∥{u_{x}}}{抖x},\frac{∥{u_{y}}}{y},\frac{∥{u_{z}}}{?z}) \) (21)

Divergence:

\( ?V(\frac{抖}{抖x},\frac{}{y},\frac{?}{抖z})?({u_{x}},{u_{y}},{u_{z}})\frac{∥{u_{x}}}{x}+\frac{∥{u_{y}}}{抖y}+\frac{∥{u_{x}}}{z} \) (22)

Curl:

\( ?V|\begin{matrix}i & j & k \\ \frac{抖}{抖x} & \frac{}{x} & \frac{?}{抖x} \\ {u_{x}} & {u_{y}} & {u_{z}} \\ \end{matrix}|=((\frac{抖{u_{x}}}{y}-\frac{抖{u_{y}}}{抖z})i,(\frac{抖{u_{x}}}{z}-\frac{{u_{x}}}{排x})j,(\frac{{u_{y}}}{x}-\frac{{u_{x}}}{?y})k) \) (23)

Acceleration:

The local acceleration caused by the unsteady flow and the displacement acceleration caused by the non-uniform flow are composed of two parts.

\( a=\frac{∥{u_{y}}}{∥t}+(?V)V \) (24)

3. Results and discussion

The optimal volume of air conditioning and the temperature setting condition of air conditioning in summer and winter are determined by the above random search algorithm. The Table 1 shows the temperature setting conditions in summer and winter.

Table 1: Air conditioning at its best

Considering that the air conditioning is affected by the location, the position of the air inlet, the number, the wind direction, the Angle, the wind speed and the air volume, the indoor temperature changes with time and space under different conditions in summer and winter are simulated. In this paper, the change of indoor temperature is analyzed from three angles: air outlet, wind speed, number of air conditioners, and placement location.

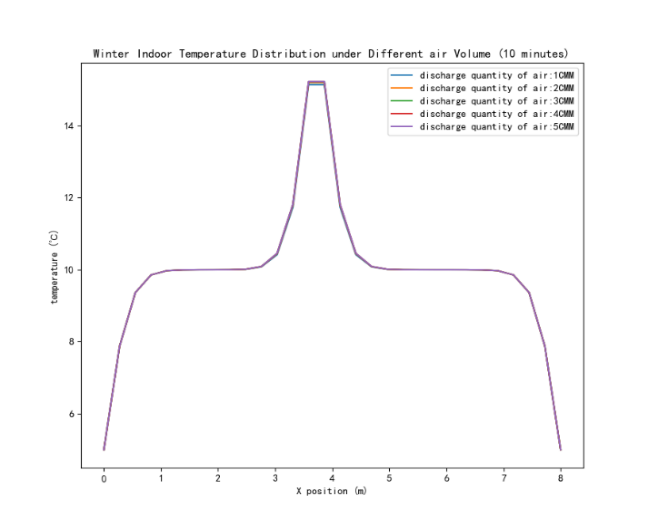
Figure 1: Variation of air output on temperature in summer (left) and winter (right)

As shown in Figure 1, The air output is 15m³/s to simulate the temperature change respectively. The results show that in summer and winter, the air output and temperature change basically coincide, indicating that the air output has little influence on the temperature effect of air conditioning.

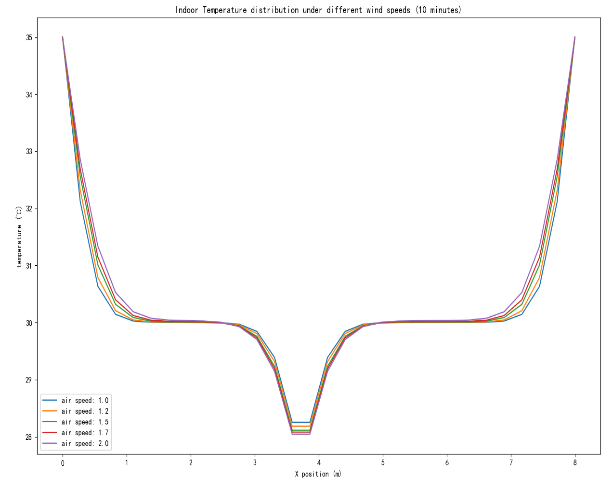
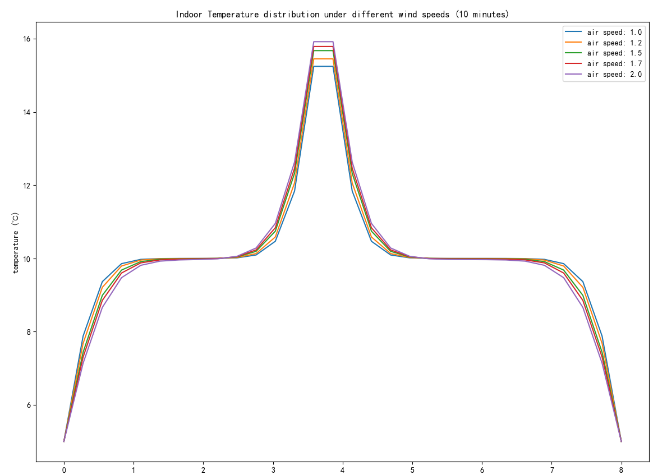
Figure 2: Changes in wind speed on temperature in summer (left) and winter (right)

As shown in Figure 2, The output air volume was taken as the initial speed of 1m/s and the step size of 0.2m/s until the cutoff of 2 m/s. The results show that the change of each output wind speed and temperature in summer and winter is obviously different, indicating that the output air volume has a more obvious influence on the temperature effect of air conditioning.

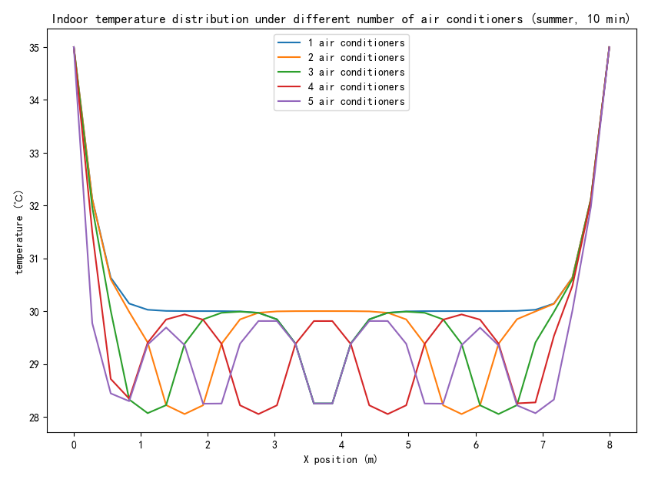
Figure 3: Changes in the effect of the number of air conditioners on temperature in summer (left) and winter (right)

As shown in Figure 3, The number of air conditioners 1-5 was taken as the research object to simulate the temperature change, and there was a large difference in the change trend, indicating that the number of air conditioners had a great influence on the temperature effect.

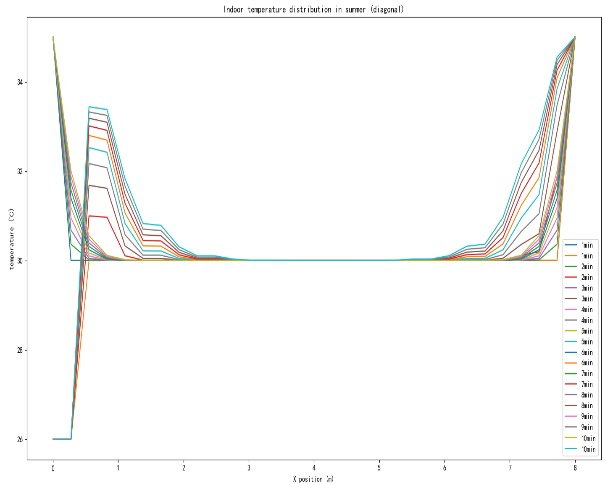
Figure 4: Changes in the effect of air conditioning on temperature on the diagonal of a room in summer (left) and winter (right)

As shown in Figure 4, Taking the span of 1-10 minutes as the research object, it can be clearly seen that there are obvious differences in the change trend, indicating that the temperature effect generated by the air conditioning is more influential when the air conditioning is on the diagonal position of the room.

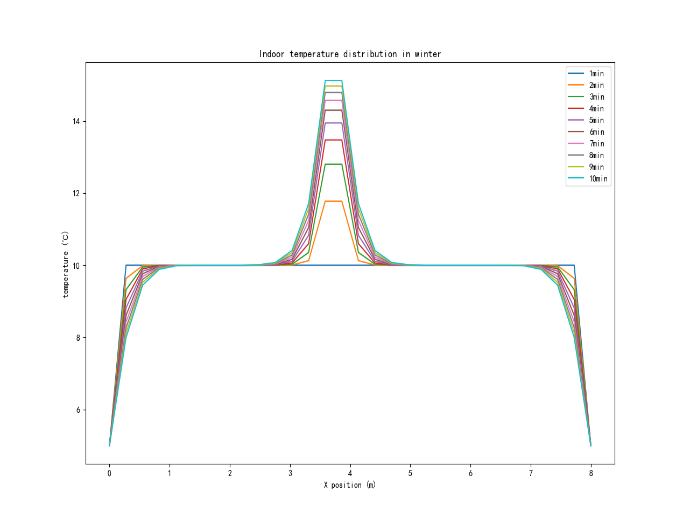
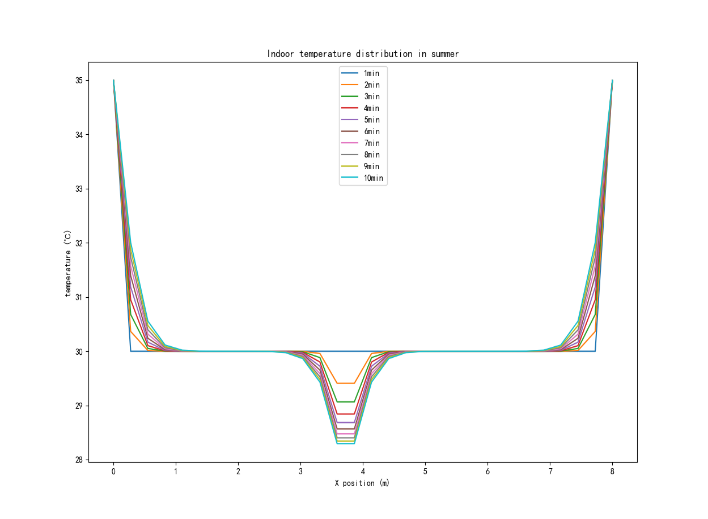
Figure 5: Changes in the effect of air conditioning in the middle of the room on temperature in summer (left) and winter (right)

As shown in Figure 5, Taking the time span of 1-10 minutes as the research object, the temperature change is simulated. The results show that in the summer and winter, the position of each air conditioner is in the middle and the temperature change situation, it is obvious that there is a significant difference in the change trend, indicating that the number of air conditioners has a relatively obvious influence on the temperature effect of air conditioning.

To sum up, the related factors that have great influence on the change of air conditioning temperature are the wind speed, quantity and spatial location of air conditioning.

4. Conclusion

In this paper, the air flow generated during the operation of air conditioning is considered, and the air circulation equation is established. On this basis, a high-performance air conditioning optimization model is established. Based on the random search algorithm, the finite difference method was used to optimize the model, and the optimal shape of the air conditioner was determined to be cuboid, and the optimal size was 0.5m×0.5m×0.5m. Then, the Lagrange algorithm was used to solve the optimal temperature adjustment effect of the simulated air conditioning in summer and winter, and the adjustment effect of the air conditioning in summer was better than that in winter.

Acknowledgements

I would like to thank Mr. Ren Chuanrong for her meticulous guidance from the framework of the paper to the detailed modification, and for putting forward many valuable comments and suggestions. Finally, I would like to express my heartfelt thanks to all the teachers who took time out of their busy schedules to review this article.