1. Introduction

The numerical solution of stiff ordinary differential equations (ODEs) poses serious challenges. In traditional explicit methods (such as the Euler method), maintaining numerical stability requires extremely small time steps due to the rapid decay or strong oscillations of certain solution components. The root cause of this issue lies in the multiscale nature of stiff problems—different solution components evolve at vastly different rates, often spanning several orders of magnitude. This disparity renders conventional explicit solvers highly inefficient. In their seminal work, Hairer and Wanner [1] emphasized the need to develop specialized numerical algorithms for such problems. As early as 1993 [2], they had established a theoretical framework for explicit and basic implicit methods aimed at non-stiff problems, where the solution components typically exhibit more uniform temporal behavior.

The primary difficulty in solving stiff problems lies in the need to compute Jacobian matrices and subsequently solve the associated linear systems. These operations are computationally intensive and prone to numerical instability. Notably, stiff systems are common in real-world applications such as chemical reaction kinetics, biomedical modeling, and circuit analysis [3], where numerical methods must simultaneously ensure stability and computational efficiency.

Among current mainstream approaches, implicit Euler and implicit Runge-Kutta methods offer favorable stability but require the repeated solution of complex nonlinear systems, leading to exponentially increasing computational costs [4]. Semi-implicit methods such as the Rosenbrock family attempt to strike a balance by combining implicit and explicit components, thereby improving computational efficiency to some extent. However, the associated computational overhead remains significant.

This research is aimed at overcoming these limitations through introducing an innovative adaptive step - size optimization strategy, which significantly enhances the efficiency of solving stiff ordinary differential equations (ODEs). Using the Rosenbrock method as a foundation, we develop an intelligent adaptive step size control algorithm that achieves an optimal trade-off between computational accuracy and efficiency. With the rapid advancement of high-performance computing, such adaptive methods are expected to demonstrate unprecedented advantages in addressing large-scale, complex problems.

2. Methodology

2.1. Standard form of stiff differential equations

The standard form of a stiff differential equation is:

$$ {\mathrm{y}}^{\mathrm{\text{'}}}=\mathrm{f}\left(\mathrm{t},\mathrm{y}\right)$$(1)

where

$$ \parallel {\mathrm{J}}_{\mathrm{f}}\parallel \gg 1$$(2)

or

$$ \mathrm{R}\mathrm{e}\left({\mathrm{\lambda }}_{\mathrm{i}}\right)\ll 0$$(3)

where $$ \mathrm{ }{\mathrm{J}}_{\mathrm{f}}$$  is the Jacobian matrix of the system, and $$ \mathrm{ }{\mathrm{\lambda }}_{\mathrm{i}}$$are its eigenvalues, which define the characteristics of stiffness [5]. Such systems exhibit a characteristic multiscale nature: some variables change rapidly, while others evolve slowly. When using explicit methods to solve these systems, maintaining numerical stability necessitates extremely small time steps, which significantly reduces computational efficiency. Therefore, in practical computations, implicit or semi-implicit methods are generally preferred.

The aim of this study is to substantially improve computational efficiency while maintaining L - stability by integrating three crucial techniques: the Rosenbrock method, adaptive step - size control, and Jacobian matrix optimization.

2.2. Algorithm framework

The entire algorithm framework consists of three core modules: stiffness detection, step size control, and Jacobian matrix optimization. These modules cooperate with each other, and the specific process is as follows:

As shown in Figure 1, the framework includes the following components:

• Stiffness detection: Determine whether the system is stiff based on the spectral radius. If stiffness is detected, a sparse solving strategy is enabled.

• Step size control: Dynamically adjust the step size based on the solution error to balance accuracy and efficiency.

• Jacobian matrix optimization: Decide whether to update the Jacobian matrix based on the frequency of changes in the solution and select either a sparse or full Jacobian depending on the stiffness.

2.3. Rosenbrock method

The Rosenbrock method is a semi - implicit scheme that is especially suitable for stiff ordinary differential equations (ODEs). It combines explicit and implicit computations and can maintain stability even when using large step sizes, providing an efficient alternative to traditional implicit methods.

The core formula is:

$$ \left(\mathrm{I}-\mathrm{h}\mathrm{\gamma }\mathrm{J}\right){\mathrm{k}}_{\mathrm{i}}=\mathrm{h}\mathrm{f}\left({\mathrm{y}}_{\mathrm{n}}+\sum _{\mathrm{j}=1}^{\mathrm{i}-1}{\mathrm{\alpha }}_{\mathrm{i}\mathrm{j}}{\mathrm{k}}_{\mathrm{j}}\right)+\mathrm{h}\mathrm{J}\sum _{\mathrm{j}=1}^{\mathrm{i}-1}{\mathrm{\gamma }}_{\mathrm{i}\mathrm{j}}{\mathrm{k}}_{\mathrm{j}}$$(4)

$$ {\mathrm{y}}_{\mathrm{n}+1}={\mathrm{y}}_{\mathrm{n}}+\sum _{\mathrm{j}=1}^{\mathrm{s}}{\mathrm{b}}_{\mathrm{j}}{\mathrm{k}}_{\mathrm{j}}$$(5)

Where  $$ \mathrm{I}$$  is the identity matrix,  $$ \mathrm{h}$$  is the step size, $$ \mathrm{ }\mathrm{J}$$  is the Jacobian matrix, and  $$ \mathrm{ }{\mathrm{k}}_{\mathrm{i}}$$  are the stage increments,  $$ {\mathrm{\alpha }}_{\mathrm{i}\mathrm{j}}$$ , γ,  $$ {\mathrm{b}}_{\mathrm{j}}\mathrm{ }$$ are the determining coefficients, s is stage number [1].

The method ensures L-stability, making it robust against rapid variations [6].

2.4. Adaptive step size control

Adaptive step size control adjusts the step size based on the local error, reducing it for rapid changes and enlarging it for slow variations to improve efficiency.

• A PI controller is employed, with the formula:

$$ {\mathrm{h}}_{\mathrm{n}+1}={\mathrm{h}}_{\mathrm{n}}{\left(\frac{\mathrm{T}\mathrm{o}\mathrm{l}}{\mid {\mathrm{e}\mathrm{r}\mathrm{r}}_{\mathrm{n}}\mid }\right)}^{\mathrm{\alpha }}{\left(\frac{\mid {\mathrm{e}\mathrm{r}\mathrm{r}}_{\mathrm{n}-1}\mid }{\mathrm{T}\mathrm{o}\mathrm{l}}\right)}^{\mathrm{\beta }}$$(6)

$$ \mathrm{\alpha }\approx \frac{0.7}{\mathrm{p}},\mathrm{\beta }\approx \frac{0.4}{\mathrm{p}}$$(7)

 $$ {\mathrm{h}}_{\mathrm{n}+1}$$  is the new time step to be used,  $$ {\mathrm{h}}_{\mathrm{n}}$$  is the current time step,  $$ {\mathrm{e}\mathrm{r}\mathrm{r}}_{\mathrm{n}}$$  is the estimated local error at the current step,  $$ {\mathrm{e}\mathrm{r}\mathrm{r}}_{\mathrm{n}-1}$$  is the estimated error from the previous step, p is the order number, and $$ \mathrm{ }\mathrm{T}\mathrm{o}\mathrm{l}\mathrm{ }$$ is the target error tolerance.

This PI control was introduced to address instability phenomena observed in stiff numerical computations [7]. Then the strategy elaborated by Hairer and Wanner [1], effectively balances responsiveness and stability by incorporating both current and historical error information.

• The error estimation formula:

$$ \mid {\mathrm{e}\mathrm{r}\mathrm{r}}_{\mathrm{n}}\mid ={\Vert {\mathrm{y}}_{\mathrm{n}+1}^{\left(\mathrm{p}\right)}-{\mathrm{y}}_{\mathrm{n}+1}^{\left(\mathrm{p}-1\right)}\Vert }_{\mathrm{\infty }}$$(8)

2.5. Jacobian matrix optimization

For large-scale stiff problems, the Jacobian is often sparse.We adopt the Curtis-Powell-Reid sparse difference method to reduce computational cost [8],

(1) Assume the system dimension is  $$ \mathrm{n}$$ , and $$ \mathrm{ }\mathrm{f}:{\mathbb{ℝ}}^{\mathrm{n}}\to {\mathbb{ℝ}}^{\mathrm{n}}$$  with the Jacobian matrix $$ \mathrm{ }\mathrm{J}$$ .

(2) Partition the variables $$ \mathrm{ }{\mathrm{y}}_1,\mathrm{ }{\mathrm{y}}_2,\dots ,\mathrm{ }{\mathrm{y}}_{\mathrm{n}}$$  into several groups, such that variables within the same group have a non-overlapping influence on the system.

(3) Perturb each group GG of variables simultaneously and compute:

$$ \mathrm{\Delta }\mathrm{f}=\mathrm{f}\left(\mathrm{y}+\mathrm{ϵ}\cdot {\mathrm{e}}_{\mathrm{G}}\right)-\mathrm{f}\left(\mathrm{y}\right)$$(9)

where $$ \mathrm{ }{\mathrm{e}}_{\mathrm{G}}$$  is the sum of the unit vectors corresponding to the variables in group  $$ \mathrm{G}$$ , and  $$ \mathrm{ϵ}$$  is a small perturbation.

(1) Approximate the Jacobian columns corresponding to the variables in  $$ \mathrm{G}$$  from  $$ \mathrm{\Delta }\mathrm{f}$$ .

(2) As a result, the number of function evaluations required to approximate the Jacobian is approximately:

$$ {\mathrm{N}}_{\mathrm{e}\mathrm{v}\mathrm{a}\mathrm{l}}=\frac{\mathrm{n}\mathrm{n}\mathrm{z}\left(\mathrm{J}\right)}{\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{l}\left(\mathrm{J}\right)}$$(10)

where $$ \mathrm{ }\mathrm{n}\mathrm{n}\mathrm{z}\left(\mathrm{J}\right)$$  is the number of nonzero elements in the Jacobian matrix and  $$ \mathrm{n}\mathrm{c}\mathrm{o}\mathrm{l}\left(\mathrm{J}\right)\mathrm{ }$$ is the number of columns.

Compared to dense solvers with complexity  $$ \mathrm{O}\left({\mathrm{n}}^3\right)$$ , sparse system solvers can achieve complexity between  $$ \mathrm{O}\left(\mathrm{n}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{n}\right)$$ , offering substantial speedups for large-scale problems.

A dynamic threshold strategy is adopted to decide when to update the Jacobian matrix [8]:

$$ \mathrm{\Delta }{\mathrm{y}}_{\mathrm{n}}={\parallel {\mathrm{y}}_{\mathrm{n}}-{\mathrm{y}}_{\mathrm{n}-1}\parallel }_{\mathrm{\infty }}$$(11)

Set a threshold  $$ {\mathrm{ϵ}}_{\mathrm{J}}$$ . If $$ \mathrm{ }\mathrm{\Delta }{\mathrm{y}}_{\mathrm{n}}>{\mathrm{ϵ}}_{\mathrm{J}}$$ , update the Jacobian. If  $$ \mathrm{\Delta }{\mathrm{y}}_{\mathrm{n}}\le {\mathrm{ϵ}}_{\mathrm{J}}$$ , reuse the previously computed Jacobian.

3. Results

In this section, the classical Robertson chemical kinetics model is used as a benchmark test case to comprehensively evaluate the performance of the proposed adaptive Rosenbrock method in solving stiff ordinary differential equations (ODEs). The study focuses on three key performance indicators: numerical stability, computational efficiency, and preservation of physical consistency. A quantitative comparison is conducted against the traditional fixed-step Rosenbrock algorithm to highlight the advantages of the adaptive approach.

3.1. Problem description and setup

The Robertson problem describes a stiff chemical kinetics system with three species and reactions that evolve on vastly different time scales. The system is defined by the following ODEs:

$$ \{\begin{array}{c}{\mathrm{y}}_0^{\mathrm{\text{'}}}=-0.04{\mathrm{y}}_0+{10}^4{\mathrm{y}}_1{\mathrm{y}}_2\\ {\mathrm{y}}_1\text{'}=0.04{\mathrm{y}}_0-{10}^4{\mathrm{y}}_1{\mathrm{y}}_2-3\times {10}^7{{\mathrm{y}}_1}^2\\ {\mathrm{y}}_2\text{'}=3\times {10}^7{{\mathrm{y}}_1}^2\end{array}$$(12)

with initial values:

$$ {\mathrm{y}}_0\left(0\right)=1,{\mathrm{y}}_1\left(0\right)=0,{\mathrm{y}}_2\left(0\right)=0$$(13)

Simulations were conducted over the interval  $$ \mathrm{t}\in \left[\mathrm{0,40}\right]$$ , using two different solvers:

Fixed-Step Rosenbrock Method: constant step size  $$ \mathrm{h}=0.01$$ .

Adaptive Rosenbrock Method: initial step size  $$ \mathrm{h}0=0.01$$ 1, dynamic PI-controller, adaptive Jacobian update.

3.2. Performance comparison

 $$ {\mathrm{y}}_0$$  Evolution

Figure 1 shows the evolution of $$ \mathrm{ }{\mathrm{y}}_0$$  over time. During the early stages (t<10), both methods align closely, confirming that the solvers are consistent in capturing the initial transient dynamics. As time progresses, the adaptive method slightly diverges from the fixed-step solution, exhibiting a faster decay in  $$ {\mathrm{y}}_0$$ ​. This behavior reflects the effect of increasing step sizes, which may trade off fine-grained resolution for efficiency.

However, the overall trend remains accurate, and the deviation remains within acceptable bounds for most practical applications. This indicates that the adaptive method balances speed and stability well during long-time integration.

 $$ {\mathrm{y}}_1$$  Evolution

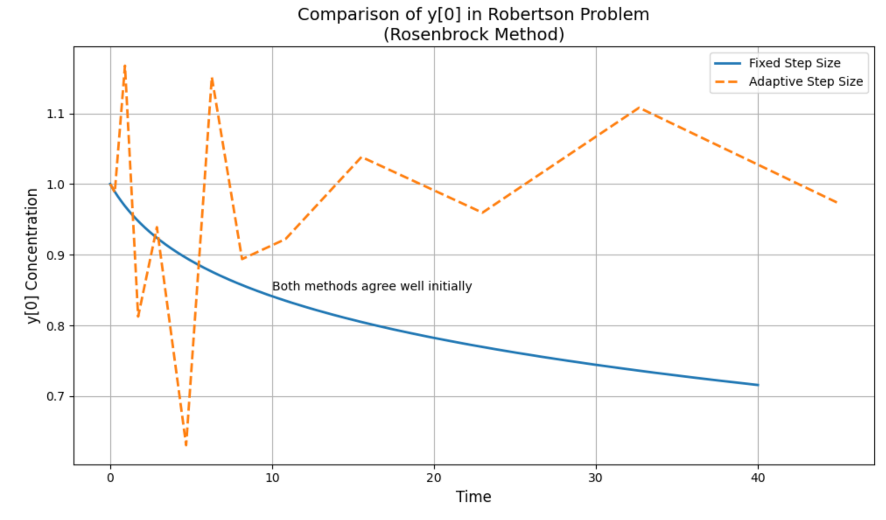
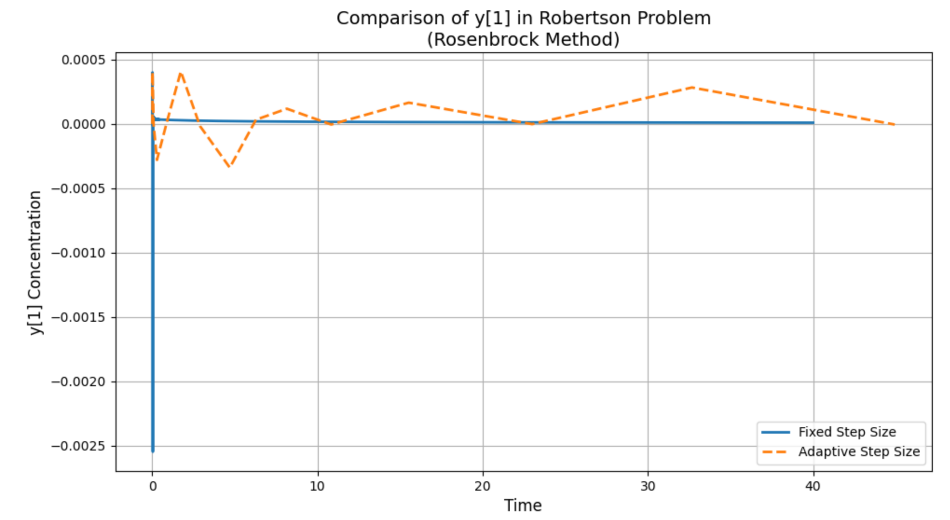
Figure 2 presents the evolution of  $$ {\mathrm{y}}_1$$ , which remains near zero but is highly sensitive to numerical instability. The fixed-step solver produces negative values in the interval $$ \mathrm{t}\mathrm{ }=\mathrm{ }30–40$$ . This results in unphysical behaviour, as the fixed-step method produces a minimum  $$ {\mathrm{y}}_1$$  value of -0.002548, violating the non-negativity requirement for chemical concentrations.

In contrast, the adaptive method preserves non-negativity much more effectively, with a minimum  $$ {\mathrm{y}}_1$$  value of only -0.000340, indicating improved numerical stability. Although still slightly negative, the error is significantly reduced, showing that adaptive time stepping is more robust in handling near-zero stiff components.

3.3. Error and efficiency evaluation

The adaptive Rosenbrock method adjusts its step size based on the PI-controller:

$$ {\mathrm{h}}_{\mathrm{n}+1}={\mathrm{h}}_{\mathrm{n}}{\left(\frac{\mathrm{T}\mathrm{o}\mathrm{l}}{\mid {\mathrm{e}\mathrm{r}\mathrm{r}}_{\mathrm{n}}\mid }\right)}^{\mathrm{\alpha }}{\left(\frac{\mid {\mathrm{e}\mathrm{r}\mathrm{r}}_{\mathrm{n}-1}\mid }{\mathrm{T}\mathrm{o}\mathrm{l}}\right)}^{\mathrm{\beta }}$$(14)

$$ \mathrm{\alpha }\approx \frac{0.7}{\mathrm{p}},\mathrm{\beta }\approx \frac{0.4}{\mathrm{p}}$$(15)

This demonstrates that the adaptive method uses small time steps during rapid transients and significantly fewer steps overall—only 15 compared to 4001 with the fixed-step method—highlighting its drastic improvement in computational efficiency.

This constitutes a 99.6% reduction in step count while maintaining comparable solution accuracy. The dramatic step count difference highlights the power of dynamic control, especially in stiff systems where slow dynamics dominate most of the integration interval.

Furthermore, Jacobian matrices are updated only when necessary, based on a dynamic threshold condition, reducing costly matrix computations. This enhances the practical efficiency of the adaptive method in large-scale systems.

3.4. Summary table

This table clearly illustrates that the adaptive Rosenbrock method outperforms the fixed-step method in terms of both efficiency and stability. The adaptive approach requires significantly fewer steps while maintaining solution accuracy and enforcing physically meaningful constraints, particularly in variables with small magnitudes.

4. Discussion

4.1. Algorithm advantages

The results indicate that adaptive step size optimization and Jacobian matrix control offer significant advantages in solving stiff ordinary differential equations. The proposed algorithm exhibits the following key features:

First, the adaptive Rosenbrock method achieves a substantial 99.6% reduction in integration steps in the Robertson problem while fully maintaining numerical stability—an especially critical feature for large-scale simulations and real-time applications. Second, the method better preserves the physical plausibility of the solution, particularly for stiffness-sensitive components such as y₁, where it significantly mitigates the appearance of unphysical negative values compared to the fixed-step approach. This outcome aligns with the findings of Savcenco [9], who demonstrated the superiority of multirate Rosenbrock strategies in preserving physical constraints during stiff transients.

In addition, the selective Jacobian update strategy strikes a good balance between computational cost and accuracy. By using a threshold-based mechanism, the Jacobian matrix is only updated when significant changes are detected, thereby avoiding unnecessary recomputation.

4.2. Limitations and challenges

Despite its clear strengths, the method also has certain limitations. The PI controller parameters currently require manual tuning, and improper settings may cause the step size to grow too significantly, resulting in minor but non-negligible violations of physical constraint. Deka and Einkemmer [10] similarly noted that poorly tuned adaptive controllers can degrade the performance of exponential integrators.

Moreover, the Jacobian optimization strategy assumes some level of sparsity or structural regularity, which may not be valid for arbitrary systems. The current error estimation approach is instructive and may not yield optimal performance across different problem domains. Pozzer et al. [11] specifically pointed out that in chemical kinetic systems with rapidly varying stiffness, naive step size adaptation strategies may still result in numerical instabilities or step rejections.

4.3. Future work

Future work may concentrate on improving the proposed algorithm by integrating adaptive learning strategies or problem - specific heuristics to automatically adjust the PI controller parameters. Additionally, integrating stiffness indicators or machine learning models could enable dynamic prediction of optimal step sizes and Jacobian update frequencies. The method can also be extended to the solution of partial differential equations (PDEs), broadening its applicability. Furthermore, exploring its parallelization potential in high-performance computing environments may significantly improve computational efficiency and promote its practical adoption in large-scale scientific simulations.

5. Conclusion

This study proposes an improved adaptive Rosenbrock algorithm for solving stiff ordinary differential equations (ODEs), incorporating dynamic step size control and selective Jacobian matrix updates. Using the classical Robertson problem as a benchmark, the method was systematically evaluated in terms of computational efficiency and numerical stability.

Experimental results demonstrate that the proposed method significantly enhances computational performance without compromising accuracy. Compared to the fixed-step Rosenbrock solver, the adaptive version reduced the number of integration steps by 99.6% while fully maintaining numerical stability. Notably, it effectively addressed non-physical behaviors such as oscillations and negative values in the y₁ component observed under fixed-step conditions.

This study presents three key innovations. First, it introduces a PI controller-based intelligent step size adjustment system that dynamically optimizes the step size in response to variations in error and stiffness during computation. Second, a novel threshold-triggered Jacobian update mechanism is proposed to minimize redundant computations by performing updates only when necessary. Finally, the method is specifically tailored for multiscale stiff systems, striking a balance between computational speed and solution reliability, thereby demonstrating strong practicality and potential for broader application.

These findings confirm that the adaptive Rosenbrock method provides an efficient and robust computational framework for stiff ODEs, particularly suited to long-term simulations or real-time applications. Future work may focus on extending this method to partial differential equations (PDEs) and differential-algebraic systems (DAEs), developing automated parameter tuning algorithms, integrating smart stiffness monitoring techniques, and exploring its synergy with machine learning approaches. This study offers a promising new solution for the numerical simulation of stiff systems.