1. Introduction

Automated control systems are the cornerstone of modern industry, where their efficient and safe operation is crucial [1, 2]. As industrial processes grow more complex, the limitations of traditional mechanism-based modeling have become clear. Data-Driven System Identification (DDSI) offers a transformative approach by learning system dynamics directly from operational data, effectively handling complex nonlinear and multivariable-coupled systems while reducing reliance on precise a priori knowledge and significantly enhancing control performance [3-5]. However, the increasing adoption of DDSI, particularly methods based on complex models like deep learning, has introduced a significant interpretability crisis in automation control [6]. High-performance, autonomous, and safety-critical control systems now suffer from opaque decision logic, functioning as "black boxes" [4, 7, 8]. This opacity extends beyond the core learning model to encompass the entire DDSI workflow, including automated data transformation and feature engineering, where generated patterns often lose their connection to original physical features, further obscuring the relationship between model inputs and outputs [9]. This opacity directly conflicts with the fundamental requirements of automated control systems for predictable behavior and verifiable control laws [2]. A control or diagnostic module that cannot explain its decision-making basis struggles to earn the trust of engineers and operators, creating substantial barriers to system commissioning, maintenance, and validation [5, 10]. This "trust deficit" has become a key bottleneck, hindering the deeper application of advanced DDSI technologies and potentially introducing serious risks from undiscovered flaws, such as vulnerability to adversarial attacks [11].

Enhancing the interpretability of DDSI models thus holds critical practical significance for the field of automation control. This endeavor is not only about realizing the full potential of data-driven methods but is also linked to improving the safety, reliability, and maintainability of automation systems. It is essential for effective human-machine collaboration, as operators need to understand control logic to maintain situational awareness and engineers require insight into model behavior for system optimization and troubleshooting [4, 12]. Even advanced paradigms like federated learning, designed for privacy and decentralization, acknowledge that a lack of model interpretability impedes trust in distributed automation scenarios [13]. Evolving industry regulations increasingly demand transparency in automated decision-making. Therefore, exploring "explainable DDSI" is an inevitable path toward more trustworthy and intelligent automation. This paper aims to provide key insights for building transparent and secure next-generation data-driven control systems, facilitating the transition from "black box" to "white box."

2. Root cause analysis of interpretability issues in DDSI

The "interpretability crisis" of DDSI models in the field of automation control is not due to a single factor, but rather to a combination of the inherent complexity of the models themselves, the unique characteristics of automated dynamic systems, and the overpursuing of performance in the current practice of DDSI.

2.1. The internal contradiction between model complexity and interpretability

The primary source of the "black-box" problem is the inherent complexity of the models used in DDSI. Traditional linear models, such as transfer function or state space models, have good interpretability because their parameters usually have a clear physical meaning, and the decision logic is traceable. However, to deal with the increasing complexity of nonlinear, high-dimensional, and multimodal data in automation control, DDSI has widely introduced machine learning models to help it deal with problems, such as deep learning models. These models, such as Multi-Layer Perceptron, Recurrent Neural Networks, Long Short-Term Memory Networks, and Convolutional Neural Networks, can achieve feature representations that are highly abstract and difficult to understand directly, utilizing multilayered nonlinear transformations, massive neurons, and connection weights [6, 14]. This high-dimensional parameter space, nonlinear mapping, and end-to-end learning model make the inner workings of the model obscure to engineers and thus naturally "black-box" [8]. Even specialized deep learning models designed for specific tasks, such as those in semantic communication, inevitably exhibit their "black-box" characteristics, making the processing difficult to fully understand and control [11].

The high-dimensional challenge is a key factor that exacerbates this problem. Many automation systems involve numerous sensors and control variables, resulting in DDSI models with extremely high-dimensional input spaces. In high-dimensional space, not only does the model structure itself become extremely complex, but also the difficulty of its internal operation grows exponentially, which is known as the "curse of dimensionality." In order to avoid the drawbacks of high dimensionality, some researchers have tried to seek a breakthrough based on the assumption that "there exists a low-dimensional effective subspace for high-dimensional black-box functions" [15]. In order to avoid the disadvantages of high dimensionality, some researchers have tried to seek a breakthrough based on the assumption that "there exists a low-dimensional effective subspace of high-dimensional black box functions" [15].

This "black-box" problem is not limited to the core learning model itself but extends throughout the entire DDSI process and may introduce opacity, especially in key aspects such as data preprocessing and feature engineering. For example, although automated data transformation and complex feature engineering methods can significantly improve the model performance, their internal transformation logic and the association between the generated new features and the original physical features are often ambiguous [9]. This means that even if the subsequent core model is relatively interpretable, the entire data processing-to-decision-making chain may lose its overall transparency due to the "black box" operation at the front end.

2.2. The intensification of interpretability issues by the characteristics of automated dynamic systems

The inherent characteristics of automated control systems (timing dependence, feedback loops, multivariate coupling, nonsmoothness, and time-varying characteristics) further catalyze and amplify the interpretability problem of DDSI models, making them far more complex than static or open-loop systems.

Strongly time-series-dependent automated systems typically process data in a time series so that current state and control decisions are not only dependent on present inputs but are also influenced by past and future data. Black-box models thus become extremely opaque in capturing and weighing historical information for decision-making. At the same time, the prevalence of feedback loops leads to the possibility that small, unexplained deviations in the model may be amplified or transmitted in the closed loop to the extent of triggering unpredictable nonlinear behaviors; and most automated systems involve a large number of interrelated variables, which are complexly coupled to each other, and the complexity of multivariate coupling makes the process of identifying and exploiting the complex relationships among variables within the black-box model difficult to be The complexity of multivariate coupling makes the process of identifying and utilizing the complex relationships between variables within the black box model difficult to be intuitively understood by researchers, which in turn hinders the isolated explanation of the role of individual components [12]; automation systems in practical applications often face non-smooth time-varying characteristics such as changes in working conditions, wear and tear and the DDSI model is required to have the ability of self-adaptation. However, when the DDSI model tries to adjust its internal logic to adapt to these changes, the first thing that needs to be solved is the transparency of its adaptive mechanism. The above issues make interpreting a black-box model for automated control far more complex and critical than interpreting a black-box model for static image classification.

2.3. The trade-off considerations between performance and interpretability in the current DDSI practice

In the practical application of DDSI, researchers and engineers often face a trade-off between performance (e.g., prediction accuracy, control effects) and interpretability [16]. In many scenarios, to pursue the ultimate performance improvement, researchers tend to adopt more complex black box models, while interpretability is regarded as a secondary goal or an afterthought. Although this "performance-oriented" tendency brings significant performance improvement in the short term, it exacerbates the "black-box" problem in the long term, making it difficult to trust, debug, and validate the models, thus limiting the applicability of these advanced technologies in the automation control field, where trustworthiness is very important. This limits the widespread deployment of these advanced technologies in the trustworthy field of automation control.

3. Interpretability challenges and implications of DDSI in automated control applications

The need for model interpretability in automated control systems goes far beyond general prediction tasks. When DDSI models are applied to key aspects of automation control, the negative impact of their lack of interpretability will fundamentally impact the design, validation, operation, and maintenance of control systems and directly threaten their safety and reliability. In this paper, we will analyze these challenges with typical application scenarios.

3.1. Controller design based on "black-box" identification models: transparency and verification challenges

DDSI-based controllers, particularly those employing deep reinforcement learning (DRL), have gained popularity for managing complex nonlinear dynamics in automation. However, their inherent "black-box" nature creates significant transparency and validation challenges.

Practitioners require clear reasoning for control decisions, yet DRL's opacity—as seen in optical network resource allocation—obscures the rationale behind actions like routing, impeding operational confidence and effective management [4]. This lack of intuitive logic comprehension hinders trust and will significantly enhance the complexity of the task. The absence of explicit mathematical representations also compounds verification difficulties for stability and robustness. Traditional formal methods become inapplicable, preventing rigorous proof of behavioral boundaries and safety under diverse operating conditions. This verification gap, exemplified by RL applications in industrial process control, obstructs real-world deployment where consistent adherence to safety constraints is paramount [5].Finally, performance degradation or unexpected behavior in these controllers complicates root cause analysis. Without insight into internal mechanisms, debugging relies on inefficient trial and error or costly retraining, escalating maintenance costs and downtime due to the failure of conventional diagnostic approaches.

3.2. Fault diagnosis based on "black-box" identification models: the challenge of decision basis and trust construction

Fault diagnosis is a key guarantee for the safe operation of automation systems. Although the DDSI model shows powerful pattern recognition ability in fault diagnosis, its "black box" characteristic brings a series of challenges, such as non-transparent diagnostic basis, lack of operator's trust, and difficulty in evaluating the generalization ability of unknown faults.

Black-box diagnostic models often fail to explain how they extract abstract fault features from raw sensor data (especially dynamic time-series data) and their correlation with physical fault patterns. For example, in industrial network security, if a deep learning-based intrusion detection system (IDS) cannot articulate the basis for identifying a traffic sequence as malicious (e.g., which protocol fields or timing features it focused on), it will be difficult for security analysts to formulate an effective defense strategy or conduct a root cause investigation [10]. Similarly, in power system fault diagnosis, if the model cannot explain how it extracts abstract information from dynamic waveforms corresponding to physical fault characteristics, engineers will struggle to trust the diagnostic results, potentially delaying repair decisions [17]. Even when visualization techniques (e.g., saliency maps) are used to interpret models, they typically produce abstract heatmaps. Engineers struggle to intuitively correlate these visualizations with actual physical processes or control logic, highlighting the fundamental challenge of explaining black-box models (See Fig. 1).

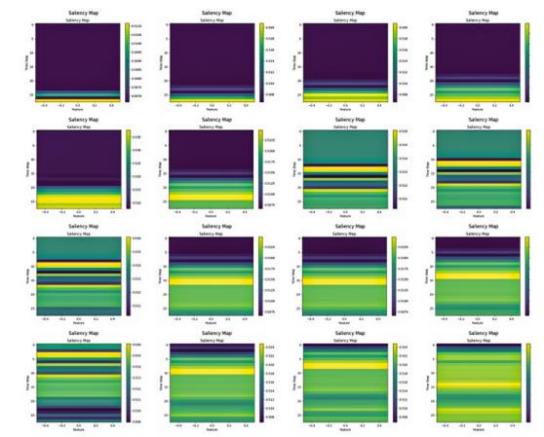
This lack of an understandable basis for diagnostic results erodes operator trust, leading to delayed responses or misjudgment of alarms, which in turn affects operational efficiency and decision quality [10]. The trust deficit is particularly prominent in distributed learning scenarios; for instance, even with advanced frameworks like federated learning that address data privacy, the opacity of the resulting diagnostic model hinders consensus and adoption among parties [13]. This pressing need for interpretability is not unique to industrial automation. In medical diagnosis, a field with similarly high stakes for safety and trust, researchers have also extensively used Explainable AI (XAI) tools like LIME and SHAP to provide a visual basis for diagnostic decisions by highlighting key regions on X-rays, thereby assisting medical professionals [19]. This confirms that bridging the gap of "black-box" models and providing a trustworthy basis for decision-making is a critical challenge in any high-stakes automated decision-making system.

Furthermore, black-box models typically reveal data correlations rather than deep causal relationships, confining diagnostic results to a "symptom" level and making it difficult for engineers to trace the physical root causes of faults [12]. This lack of insight into the internal diagnostic logic also makes it extremely difficult to assess the model's generalization ability to new or dynamically changing fault modes, often leading to poor performance in real-world operations, while engineers are left unable to effectively troubleshoot or improve the model.

3.3. Potential risks to the full life cycle of automated systems from a lack of interpretability

In summary, the lack of interpretability of DDSI models is not limited to a single technical issue but poses a potential risk throughout the entire lifecycle of an automated system. From verification and validation in the design phase to user trust and acceptance in the deployment phase, to debugging, maintenance, and troubleshooting in the operation phase, and ultimately to knowledge transfer, the unexplainable "black box" can introduce uncertainty, increase operational risk, and hinder system optimization. This systemic impact makes interpretability a key bottleneck in driving data-driven automation to maturity and widespread adoption.

4. Analysis of existing methods for improving the interpretability of DDSI and their applicability in automation field

In the face of the "black box" crisis caused by DDSI models in automation control, academics have paid attention to and actively explored a variety of methods to enhance interpretability. As shown in Fig. 2, these methods integrate interpretable (white/grey-box) and high-performance (black-box) models through distinct configurations (e.g., serial, parallel, ensemble) to balance performance and interpretability. This section critically examines these mainstream approaches, focusing on their applicability and limitations when applied to automated dynamic systems.

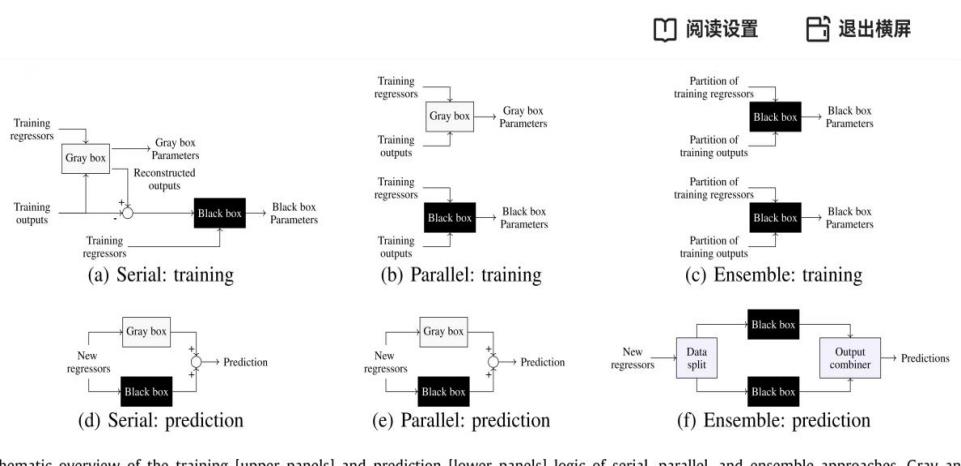
4.1. Intrinsically interpretable models: limitations in complex systems

Intrinsically Interpretable Models (IIMs) are designed for transparency from the outset, using structures and logic which are easily understood by engineers (e.g., linear regression, decision trees). In DDSI, Symbolic Regression (SR) exemplifies this approach, automatically discovering mathematical equations describing system dynamics. SR transforms system identification into a search problem: it explores combinations of basic mathematical functions (+, -, ×, ÷, exp, sin, etc.) from a predefined library, iteratively optimizing them to find equations that balance accuracy with simplicity. Crucially, SR outputs directly interpretable mathematical expressions, eliminating the need for post hoc explanation. A key SR method is Sparse Identification of Nonlinear Dynamics (SINDy). SINDy identifies concise nonlinear differential equations from data by leveraging sparse regression (e.g., L1 regularization). This enforces model sparsity, reflecting the physical principle that most systems are governed by only a few dominant terms, yielding interpretable and physically meaningful equations [20]. Calapristi et al. further emphasizes the "inherent interpretability" of the SR model (including SINDy), as it directly generates human-readable mathematical equations and applies them to nonlinear dynamic system identification, demonstrating their key role in understanding the system process [21].

However, IIMS often lack accuracy in complex automation control systems. Their simple structures (e.g., equations, rules) struggle to capture complex nonlinearities, high-dimensional interactions, and time-varying dynamics. When extreme performance is required, IIMs typically cannot match the accuracy of black-box models. This inherent trade-off between simplicity/interpretability and expressive power/accuracy is a critical limitation for IIMs in complex automated systems.

4.2. Post-hoc interpretation techniques: challenges from dynamic systems

Post-hoc Explanation Techniques aim to explain the decisions of a black-box model through external methods without changing the structure of the original black-box model. These methods have the advantage of being model-agnostic and can be applied to any black-box model, so they are widely used in practice. Mainstream ex-post interpretation techniques include Locally Interpretable Model-Independent Interpretation (LIME), Shapley Additive Properties Interpretation (SHAP), as well as Partial Dependency Diagrams (PDPs) and Individual Conditional Expectation Diagrams [22, 23].In the automation control field, these post hoc interpretation techniques have been attempted to be applied to explain complex DDSI models. For example, Shoukat et al. used SHAP to explain the decisions of a deep learning IDS in an industrial network threat detection system to improve transparency and trust [10]. Ukwuoma et al. also applied SHAP, LIME, and PDP to explain the diagnostic results of a data-driven model in power system fault diagnosis [17]. Calapristi et al. also used SHAP in their study to aid in the interpretation of inherently interpretable SR models [21].

While post-hoc interpretation techniques like LIME and SHAP work well for static tasks, they fall short when applied to automated dynamic systems. These methods inadequately capture temporal dependencies, feedback loops, and long-term system evolution, typically offering only static or aggregated feature importance. This makes them unable to explain continuous control decisions. Furthermore, their reliance on approximations often yields low-fidelity explanations inconsistent with the original model's behavior. Such unreliable interpretations pose significant risks in safety-critical control environments. The fundamental limitation is that these techniques explain "why this prediction?" rather than addressing the critical control questions: "why this action now?" and "how will it impact future dynamics and stability?". For example, while SHAP might identify state features influencing a single DRL controller action, it fails to explain the underlying learning policy or the action's effect on long-term returns [4].

4.3. Physical knowledge-guided discrimination methods: potential but immature

Incorporating physical knowledge into data-driven models, often referred to as "gray-box modeling" or "physics-informed learning," is a promising direction for improving interpretability. This approach aims to combine the flexibility of data-driven methods with the transparency of physical models. Physics-Informed Neural Networks (PINNs) are a prominent example, using physical laws as part of the loss function to guide the network toward solutions that conform to these principles [24]. In the field of automation control, physics-informed DDSI has made significant progress. For instance, Leoni et al. proposed a "Mixture of Experts (MoE)" framework that enables interpretable data-driven modeling by fusing gray-box and black-box models [16]. Similarly, Wu et al. designed a "Mechanism-Enhanced Neural Network (MENN)" for fault diagnosis in power electronic converters, which integrates system mechanisms into the data-driven model to significantly improve diagnostic accuracy and decision interpretability [24]. Patel also noted that integrating domain knowledge can enhance the interpretability of Reinforcement Learning [5].

While promising, physics-informed approaches face maturity and usability challenges in complex automation systems. Key hurdles include: 1) Difficulty formalizing complex domain knowledge (e.g., multi-physics coupling, nonlinear dynamics) into embeddable constraints; 2) Lack of robust methods for integrating heterogeneous physical knowledge with data-driven models; 3) Limited generalizability where physical principles often apply only to specific subsystems or operating conditions. Traditional robot dynamics models handle rigid-body motion well but struggle when interacting with deformable objects or unknown friction environments. Incorporating complex contact mechanics or tribology into frameworks like PINNs would significantly increase difficulty and computational cost. Worse, it may require new empirical models with their own interpretability issues, limiting the physics-informed approach's generalizability and extensibility.

4.4. Major shortcomings of current interpretable methods in automated control applications

Taken together, current methods for enhancing DDSI interpretability still have significant shortcomings in automation control applications. Inherently interpretable models are limited in their ability to express complex dynamics; post hoc interpretation techniques are only suitable for static classification or regression tasks when dealing with timing, feedback, and control decisions, and are difficult to provide in-depth and reliable interpretations; and physical knowledge-guided approaches, although promising, are limited by the complexity of their knowledge formalization and fusion in some complex automation scenarios at this stage. Together, these limitations constitute a major obstacle on the road to "transparency" in the field of automation control.

5. Building more transparent and trustworthy automated data-driven system

In face of the interpretability crisis faced by DDSI in automation control, future research should move beyond the paradigm of purely pursuing performance to building intelligent automation systems that are inherently more transparent and trustworthy. This requires us to innovate at the core technology level and closely integrate with the unique requirements of automation control.

5.1. Deep integration of physical knowledge and domain priors

To solve the "black box" problem in DDSI, a key approach is to integrate engineering and priori knowledge of automation control into the data-driven model to build a "deep gray box" model. Future research will focus on how to embed priori knowledge of control theory (e.g., system structure, causality, stability conditions, conservation laws) into the learning process of DDSI in a more structured and flexible way so that it can follow the physical laws while learning the data patterns, improving physical consistency, generalization ability and interpretability of the model.

PINNs have shown the potential to incorporate physical knowledge by using the laws of physics as part of the loss function [25]. Chen et al. further explored the application of PINNs in the predictive control of nonlinear models [26]. They proposed to extend neural networks that incorporate physical information to model ordinary differential equations so that they can be adapted to the control task and have physical interpretability. This approach not only improves the physical interpretability of the model but also achieves static-free control and significantly reduces the control stabilization time. This deep fusion not only improves the model performance but also radically enhances its transparency and provides a trusted decision basis for automation control. The future challenge is how to extend these successful practices to a wider range of automation control scenarios and address the challenges of formalizing and fusing complex domain knowledge [5].

5.2. New paths to enhance the interpretability of automated systems

The challenges that current XAI methods face in explaining automated dynamic systems point precisely to the direction of future core breakthroughs. The way forward for research lies not in the simple porting of generic XAI tools designed for static prediction, but in the development of new methods that can reveal dynamic causality and explain control strategies.

A highly promising direction is shifting explanations from "feature attribution to dynamic causal inference." Current methods like SHAP and LIME answer "Which input features influenced this prediction? " However, automation control requires answering: "Why does this control action cause this dynamic system behavior? " This demands XAI capable of causal reasoning. Future work could leverage Counterfactual Explanations to quantify the causal impact of control decisions by systematically exploring: "How would the system's future state change if a different action were applied?" [27]. In addition, combining data-driven approaches with the physics of automated systems enables the systematic generation and verification of causal hypotheses, thereby helping engineers identify the physical root causes of failures rather than just identifying symptoms [12].

Another promising approach uses model distillation/imitation learning to explain complex control strategies. Instead of interpreting internal mechanisms of black-box controllers (e.g., DRL), we train intrinsically interpretable "student" models—such as sparse symbolic regression models or simplified rule sets—to mimic the "teacher" controller's decision behavior [20]. As attempted by Cedeño et al., by analyzing this interpretable "student" model, engineers can approximate the control logic and dynamic behavior of the black box controller [4]. This field, known as Explainable Reinforcement Learning, provides a practical path to understanding complex, self-learning control strategies and is key to building trustworthy autonomous systems [28].

Future research should take visualization as a powerful explanatory paradigm for human users. In addition to generating mathematical equations or feature contributions, transforming abstract decision-making processes into an intuitive visual language is an effective way to improve the efficiency of human-computer interaction. For example, Mtetwa et al. proposed to use Generative Adversarial Networks (GANs) to generate Saliency Maps to visually emphasize the key market factors that affect the decision-making of DRL intelligences [18]. This suggests designing interactive visual interfaces that embed abstract interpretations (e.g., SHAP values, causal chains) within engineering contexts like P&IDs and state trend diagrams. By doing these, explanations become linked to real system representations, helping engineers understand things more easily.

6. Conclusion

DDSI has undoubtedly brought profound changes to automation control. However, complex models represented by deep learning, due to their "black box" nature, have also triggered an "interpretability crisis" in the highly safety-, reliability-, and predictability-demanding automation field. This paper analyzes that this crisis not only stems from model complexity but is also amplified by the dynamic, feedback, and coupling characteristics of automation systems. By examining application scenarios such as controller design and fault diagnosis, this paper demonstrates how the lack of interpretability impacts system verification, debugging, operation and maintenance, and trust building, becoming the core bottleneck for the in-depth application of advanced DDSI technology in critical tasks. At the same time, this paper critically reviews existing methods to enhance interpretability (intrinsic interpretable models, post-hoc explanation techniques, and physics knowledge guidance), and points out their limitations in explaining complex automation dynamic systems. In future research, solving the black box problem depends on developing interpretability methods oriented towards the characteristics of automation. Core directions include: deepening explanations from feature attribution to dynamic causal inference to reveal the deep logic of the system; or using model distillation or imitation learning and other means to explain complex control strategies.

In conclusion, addressing the interpretability challenge is the key to promoting the maturity and wide application of data-driven automation technology. Future research requires the joint efforts of the academic and industrial communities to continuously break through in interpretability theory, methods, and applications, and ultimately build transparent, trustworthy, safe, and efficient next-generation data-driven automation control systems.