1. Introduction

Modern cryptographic systems, such as integer factorization (RSA), Digital Signature Algorithm (DSA), and Elliptic Curve Cryptography (ECC) are built upon the computational hardness of problems like integer factorization and discrete logarithms [1, 2]. However, this foundational security assumption is under threat from quantum computing. As Lindsay notes, “a large-scale, fully functional, universal quantum computer could factor very large numbers in a matter of hours”—rendering current encryption protocols obsolete [3]. Shor’s algorithm [4], developed in 1994, demonstrated the theoretical possibility of exponentially faster factorization, turning what would take “six quadrillion years” for classical machines into a solvable problem within hours [3].

This looming disruption has accelerated the field of post-quantum cryptography (PQC), which seeks quantum-resistant alternatives. Some promising candidates include lattice-based encryption (such as NTRU) and hash-based signature schemes (such as SPHINCS+)[5, 6]. These methods are not vulnerable to known quantum attacks like Shor’s or Grover’s algorithms[6]. As Lindsay explains, cryptographers are actively “fielding countermeasures” that rely on “different mathematical problems believed to be intractable for both classical and quantum computers” [3].

The urgency of this transition is amplified by global investment, especially for countries that are racing to “operationalize quantum technology” for both defense and offense [3]. As Kumar et al. emphasize, cryptographic systems must be evaluated not only by theoretical security but also by “performance metrics like key size, block modes, and throughput” [6].

This paper explores the mathematical foundations of PQC, the vulnerabilities exposed by quantum algorithms, and the challenges of deploying practical, future-proof cryptographic infrastructures.

2. Pre-quantum cryptography

Classical cryptographic systems, such as RSA, DSA, and ECC, have long provided the backbone of secure digital communication. These schemes rely on the intractability of specific mathematical problems, such as integer factorization (RSA), discrete logarithms (DSA), and elliptic curve discrete logarithms (ECC). The old-fashioned computers that people use today are hard to invert the key to these algorithms. For instance, RSA’s security model is conceptually simple yet mathematically robust. It depends on the computational difficulty of factoring a large semiprime number n = pq, where p and q are randomly chosen large primes. The algorithm relies on key pairs (e,n) for encryption and (d,n) for decryption, linked by the relation ed ≡ 1 mod φ(n), where φ(n) = (p − 1)(q − 1) is Euler’s totient function. Encryption is performed by computing c ≡ me mod n, and decryption recovers the original message m ≡ cd mod n [1]. Because of the wide use of RSA, in this paper, we will use RSA as the representative pre-quantum cryptographic system.

The strength of RSA lies in the perceived infeasibility of factoring n to recover p and q, thereby computing φ(n) and deducing d. While brute-force methods such as trial division are computationally absurd for large key sizes, more advanced algorithms have been developed to attack the problem. Chief among them is the General Number Field Sieve (GNFS), currently the most efficient known classical algorithm for factoring large integers. GNFS generalizes ideas from the Quadratic Sieve by operating over algebraic number fields, finding smooth relations that map to congruences of squares modulo n. These congruences can potentially be used to factor n if they yield non-trivial square roots [7].

Despite its sophistication, GNFS remains sub-exponential in complexity. Its expected runtime is approximately

$$ \exp \left({\left(\frac{64}{9}\right)}^{\frac{1}{3}}{\left(\log \mathrm{n}\right)}^{\frac{1}{3}}{(\log \log \mathrm{n})}^{\frac{2}{3}}\right)$$(1)

[8] making it computationally infeasible to factor RSA keys of 2048 bits or higher using classical resources. Factoring even 512-bit RSA keys with GNFS can require thousands of core-hours, making such attacks impractical for ordinary adversaries. As a result, RSA is safe before the threat of quantum computer.

The next section will introduce one revolutionary algorithm, Shor’s algorithm, and explain how quantum computers can utilize this algorithm to attack the known cryptographic systems.

3. Imminent threat

As previously discussed, classical computers do not currently pose a significant threat to widely used cryptographic systems such as RSA, largely due to the computational difficulty of factoring large semiprime numbers. However, the emergence of quantum computing introduces an imminent threat to the foundations of modern cryptography.

3.1. Shor’s algorithm

In 1994, Peter Shor developed a quantum algorithm that factors large integers exponentially faster than classical methods. By reducing factoring to order finding and applying the quantum Fourier transform, Shor proved that quantum computers could break RSA, sparking major interest in quantum computing and post-quantum cryptography [4].

The steps of Shor’s algorithm are straightforward:

(1) Random Selection: Choose a random integer a such that 1 < a < N and gcd(a,N) =1. If gcd(a,N) ≠1, then a is already a nontrivial factor of N.

(2) Period Finding: Define the function f(x) = ax mod N. Use a quantum computer to determine its period r, the smallest positive integer for which

$ar\equiv 1(modN)$(2)

(3) Check Even Period: If r is odd, the algorithm fails and must restart with a different value of a. If r is even, proceed to the next step.

(4) Compute Potential Factors: Calculate

$gcd(ar\mathrm{/}2\pm 1,N)$(3)

If either of these values yields a nontrivial factor (i.e., not 1 or N), then the factorization is successful.

(5) Repeat if Necessary: If no factor is found, repeat the process with a new random base a.

The mathematical logic behind the key step, step 3, is on the elementary number theory level. From step 2, once the period r of the function f(x) = ax mod N is found, we observe that ar ≡ 1 (mod N). This implies that

$ar-1\equiv 0(modN)$(4)

meaning N divides ar − 1. Using algebraic factorization, it can be expressed this as

$ar-1=(ar\mathrm{/}2-1)(ar\mathrm{/}2+1)$(5)

Therefore, we have

$(ar\mathrm{/}2-1)(ar\mathrm{/}2+1)\equiv 0(modN)$(6)

If r is even and ar/2 ̸≡ ±1 (mod N), then it is likely that one of the terms ar/2 − 1 or ar/2 + 1 shares a nontrivial factor with N. Thus, computing the greatest common divisors

$gcd(ar\mathrm{/}2\pm 1,N)$(7)

may yield a nontrivial factor of N, allowing successful factorization.

3.2. Quantum computer and Shor’s algorithm

The second step involves finding the period of the random integer a, which is computationally difficult for classical machines with large primes. As a result, Shor’s Algorithm is applicable with the emergence of quantum computers. Quantum computers use superposition and Quantum Fourier Transform to efficiently find the period.

The quantum part of Shor’s algorithm begins by preparing a superposition of all integers q less than n. A quantum computer then evaluates the modular exponentiation function aq mod n simultaneously for all q < n, resulting in an entangled state that maps each q to its corresponding output p ≡ aq mod n. Upon measurement, the system collapses to a random value p, leaving a superposition of all q values that satisfy aq ≡ p mod n. Importantly, if ar ≡ 1 mod n, then this modular function is periodic: for any integer q,

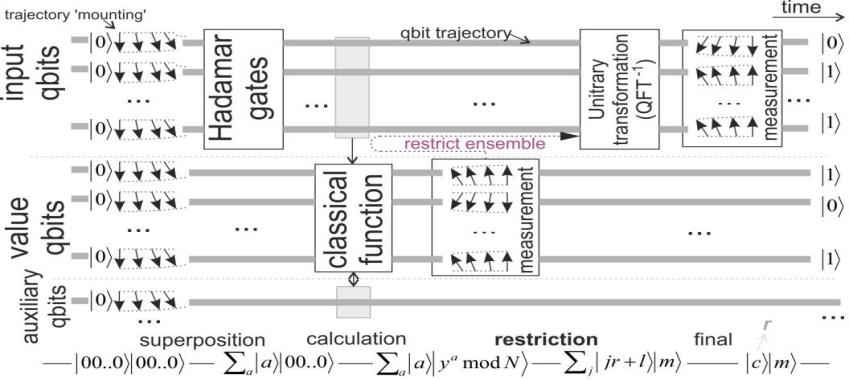
aq+r ≡ aq mod n. As a result, the remaining superposition includes values of q that are spaced apart by a period r. The quantum Fourier transform (QFT) is then applied to this periodic state to extract the frequency component corresponding to  $$ \frac{1}{\mathrm{r}}$$ , thereby revealing the period r with high probability. This period-finding step is the core quantum speedup in Shor’s algorithm, enabling exponential improvement over classical factoring methods [9]. Figure 1 is a simplified visual illustration of how to find the period for a Quantum computer. The QFT (quantum Fourier transform) extracts the periodicity from the superposition of quantum states resulting from modular exponentiation.

Shor’s algorithm represents a fundamental shift in the threat landscape of modern cryptography. By enabling efficient integer factorization in polynomial time[10], it directly compromises the security of RSA, which relies on the classical difficulty of factoring large semiprimes. In contrast, the best classical algorithm, the General Number Field Sieve, remains sub-exponential; for example, factoring a 232-digit number in 2009 required computational effort equivalent to 2000 years on a single-core processor. Although Shor’s algorithm is not yet widely deployable due to its high resource demands—requiring approximately 2n+3 logical qubits to factor an n-bit number—the rapid progress of quantum hardware development is closing that gap. Since modern RSA implementations often use 2048-bit keys, a successful attack would require over 4000 logical qubits, whereas today’s quantum computers possess only about 1000 physical qubits. Although we only touch on RSA and prime factorizations, it also poses threats to other systems like the finite-field Diffie–Hellman key exchange, and the elliptic-curve Diffie–Hellman key exchange. The threat may not be immediate, but the trajectory of quantum research suggests that this barrier could be overcome within the coming decades.

4. Post-quantum computer cryptography: hash function based cryptographic scheme

In response to the looming threat, the field of post-quantum cryptography (PQC) has emerged, aiming to develop cryptographic schemes that are resistant to both classical and quantum attacks. Researchers have proposed various families of post-quantum cryptosystems, including lattice-based cryptography, code-based cryptography, multivariate polynomial schemes, isogeny-based cryptography, and hash-based digital signatures [6]. In this section, we focus specifically on hash-based cryptography, with particular emphasis on the SPHINCS+ digital signature scheme—one of the leading candidates in the NIST postquantum cryptography standardization process.

4.1. Hash function

A hash function is a fundamental cryptographic primitive that takes an input of arbitrary length and returns an output of fixed length. Formally, a hash function H : X →Y maps a potentially infinite domain X (e.g., all binary strings) to a finite codomain Y (e.g., 256-bit strings).

Three foundational properties are crucial to cryptographic hash functions:

• Non-injective: Since the output space is fixed and the input space is vast, many different inputs will inevitably map to the same output. This non-injectivity is by design, but must be managed securely.

• Pre-image resistance: Given a hash value h, it should be computationally infeasible to find any input x such that H(x) = h. This ensures the hash function is one-way and prevents attackers from reversing hashes.

• Avalanche effect: A small change in input should result in a dramatically different output. This sensitivity is vital for maintaining unpredictability and security. One metaphorical example that is not based on real Hash function would be the following:

Hash("hello") → 1a79a4d60...

Hash("Hello") → f7c3bc1d8...

Prominent cryptographic hash functions include SHA-2 (e.g., SHA-256) and SHA-3. These functions are designed to satisfy the above properties while being efficient to compute. In practice, hash functions are used across modern cryptography: for message authentication codes (HMAC), password hashing, blockchain consensus, and digital signature schemes. Notably, they serve as the core building blocks in several post-quantum cryptographic proposals due to their minimal algebraic structure and resistance to known quantum attacks (with Grover’s algorithm offering only a quadratic speedup)[11].

To illustrate their behavior metaphorically, a good hash function can be imagined as a super blender. No matter what ingredients (input) you throw in, it produces a uniform, fixed-size smoothie (digest). You cannot reverse-engineer the ingredients from the smoothie (pre-image resistance), and even adding a pinch of salt can change the flavor entirely (avalanche effect). This irreversibility and sensitivity make hash functions a powerful and versatile tool in both classical and post-quantum cryptography.

4.2. SPHINCS+

SPHINCS+ is a stateless, hash-based digital signature scheme designed to be secure even against quantum adversaries. Unlike traditional public-key cryptographic systems such as RSA or ECC, SPHINCS+ does not rely on number-theoretic assumptions. Instead, it uses only cryptographic hash functions, making it a strong candidate in the post-quantum cryptographic landscape.

To understand how SPHINCS+ works, consider a simple scenario: Alice wants to sign a message and send it to Bob in a way that Bob can verify its authenticity—even if an attacker like Eve has access to a quantum computer. Alice uses SPHINCS+ to generate a signature, which she sends to Bob along with the message and the public key. Bob verifies the signature using only hash function operations based on Message M, Signature σ, Public key.

4.2.1. Setup and parameters

SPHINCS+ begins with the selection of parameters. The most important include:

• Security parameter n (e.g., 256 bits for practical use).

• Winternitz parameter w, typically a small power of two (e.g., 4 or 16).

These are used to compute the lengths of hash chains:

$$ {\mathcal{l}}_1=\lceil \frac{\mathrm{n}}{{\log }_2\mathcal{w}}\rceil ,\mathrm{ }{\mathcal{l}}_2=\lfloor {\log }_{\mathcal{w}}\left({\mathcal{l}}_1\left(\mathcal{w}-1\right)\right)\rfloor +1,\mathrm{ }\mathcal{l}={\mathcal{l}}_1+{\mathcal{l}}_2$$(9)

Example: Let n = 8 and w = 4, then ℓ1 = 4, ℓ2 = 3, so total ℓ = 7. These determine the number of hash chains used in a signature.

4.2.2. Key generation and the merkle tree

For each signature, the signer generates ℓ secret keys sk0,...,skℓ−1. Each key is hashed w − 1 times to form the corresponding public key element: pki = H(w−1)(ski).

All pki values are organized into a Merkle tree. The root of this tree becomes the overall public key.

Example: If w = 4, then each pki = H(H(H(ski))). The seven pki values are used to construct a binary Merkle tree, with the root serving as the public key.

4.2.3. Signature generation and verification

The signature corresponds to partially hashed versions of each ski, based on how the message is encoded. In the example above, suppose the message maps to an index vector like

[1,2,0,3,2,1,0], where each entry tells how many hash steps to apply to the respective ski.

• σ0 = H(sk0)(1 step)

• σ1 = H(H(sk1))(2 steps)

• σ2 = sk2(0 steps)

• etc.

The full signature is then: σ = [σ0,σ1,σ2,σ3,σ4,σ5,σ6].

The public key consists of the fully hashed chains: pki = H(w−1)(ski).

Verification involves applying the remaining hash steps to each σi so that it matches the corresponding pki.

Below is the visualization of the process, illustrating how Alice generates public key and the signature, and how Bob can utilize the signature to verify the public key for the first secret key:

sk0 → H → σ0 → H → H → pk0

(Signature) (Public Key)

Bob can perform this process for all the signatures and public keys to verify whether the sender is truly from Alice, not the imposer Eve.

4.3. Quantum resilience of SPHINCS+

Unlike traditional asymmetric algorithms such as RSA, ECC, and Diffie–Hellman—which rely on number-theoretic problems like integer factorization and discrete logarithms—hash-based cryptography does not depend on algebraic structures that can be exploited by quantum algorithms. This is what makes hash-based cryptography, such as SPHINCS+, remains a strong candidate for PQC.

As noted in Bavdekar et al. [6], Shor’s algorithm breaks RSA and ECC by solving their hard problems in polynomial time, while Grover’s algorithm gives only a quadratic speedup for brute-force attacks. Hash functions, which are the foundation of SPHINCS+, are primarily affected by Grover’s algorithm. This means that a quantum adversary can reduce the brute-force cost of breaking a hash function from 2n to 2n/2. As a result, increasing the hash output size (e.g., using SHA-256 instead of SHA-128) is sufficient to retain strong post-quantum security.

SPHINCS+ uses a layered approach combining Winternitz One-Time Signatures (WOTS+), Merkle trees, and a few-time signature schemes to create a stateless, secure, and versatile signature mechanism. Its security relies solely on the classical properties of the underlying hash function: pre-image resistance, second pre-image resistance, and collision resistance. These properties are well understood and do not offer exploitable patterns that quantum algorithms can meaningfully target beyond brute-force improvement.

5. Future challenges and considerations

Post-quantum cryptography stands at the intersection of urgent necessity and cautious optimism. As quantum computing threatens to undermine widely deployed cryptographic standards such as RSA and ECC, there are still some promising candidates to counter these threats, such as the hash-based cryptography.

However, the path to widespread adoption is far from complete. Several key challenges remain. First, the trade-off between security and efficiency continues to limit deployment. For instance, stateless hash-based schemes, while highly secure, often incur large signature sizes and slower signing processes. Addressing these constraints without compromising robustness is a central engineering goal.

Second, real-world integration presents practical issues. Cryptographic systems must be compatible with diverse hardware, protect against side-channel attacks, and remain efficient across billions of devices. The assumptions made in theoretical security models do not always hold in implementation, especially in environments involving virtualization, shared memory, or limited entropy sources.

Third, standardization and interoperability are essential for global adoption. Institutions like NIST, IETF, and ISO are actively evaluating and refining candidate algorithms, but the timeline for finalization and deployment remains uncertain. Ensuring that postquantum schemes can fit seamlessly into existing protocols such as TLS, VPNs, and firmware updates will require careful coordination.

Finally, continued cryptanalytic scrutiny is critical. Robust cryptography is built not just by proposing new systems, but by withstanding years of rigorous analysis. As highlighted in recent literature, the history of cryptography is filled with examples where promising constructions failed under pressure. Ongoing research must not only propose, but also test, refine, and occasionally retire insecure systems [12].

The future of cryptographic security hinges on striking a careful balance between innovation and caution. Post-quantum systems like SPHINCS+ are promising candidates, but their success depends on sustained research, practical improvements, and responsible deployment. We are in a race not just against the clock of quantum advancement, but toward building a secure and adaptable cryptographic future.