1. Introduction

In recent years, with the large-scale integration of renewable energy such as wind power, the frequency regulation mechanism of the power system that relies on the inertia of synchronous generators is facing severe challenges. Due to the general use of power electronic converter access mode in wind power generation systems, it does not have physical inertia, resulting in the overall inertia level of the system decreasing, the frequency response performance deteriorating, and the frequency modulation ability decreasing [1].

Doubly-fed induction Generators (DFIGs) have emerged as the dominant configuration for grid-connected wind turbines due to their variable-speed operation, high energy capture efficiency, and reduced converter capacity requirement. Compared with full-converter topologies, DFIGs offer a more cost-effective and controllable solution with the potential to participate in primary frequency regulation.

To enable frequency regulation capabilities in wind power systems, advanced control strategies must be employed to actively modulate output power, emulate inertia, or directly participate in frequency regulation. This paper proposes a Lyapunov-based frequency control strategy tailored to the dynamic behavior of DFIGs [2], ensuring asymptotic stability and robust frequency support for wind-integrated power systems.

Compared with other wind turbine technologies such as squirrel cage induction generators (SCIG) and permanent magnet synchronous generators (PMSG), DFIGs offer superior controllability, lower converter cost, and the ability to support grid services like frequency regulation.

This study leverages explicitly the controllability of DFIGs to design a Lyapunov-based frequency regulation strategy, which improves the dynamic response capability of wind-integrated systems. This work addresses a critical wind power frequency control gap by combining nonlinear stability theory with practical DFIG system modeling. While the results show significant improvements, future research could explore real-time implementation challenges, robustness under parameter uncertainties, and extension to multi-machine systems.

2. Literature review

In recent years, with the continuous expansion of the scale of high proportion of renewable energy grids, the research on the participation of wind power generation systems on the participation of wind power generation systems in grid frequency regulation has become an essential topic in the field of power system control [3]. The existing literature shows that the wind power frequency modulation control strategy mainly focuses on three types of methods, and the various techniques show significant differences in dynamic response characteristics, robustness, and implementation complexity.

2.1. Research status of traditional proportional-integral control methods

As a widely applied fundamental control scheme in the industry, the PI controller has long dominated the control of wind power converters due to its simple structure and clear physical meaning of parameters. However, numerous empirical studies have pointed out the inherent limitations of fixed-parameter PI controllers: when dealing with significant disturbances in the power grid, their response speed is limited by the integral time constant, and their control performance is sensitive to changes in the operating point. It is particularly noteworthy that when the penetration rate of wind power exceeds 30%, traditional PI control struggles to meet the stringent requirements of modern power systems regarding frequency deviation [4].

2.2. Development of virtual inertia control technology

Researchers have proposed the innovative concept of virtual inertia control to overcome the inherent differences in inertial response between wind turbines and synchronous generators. The core of this technology lies in simulating the rotor motion equations of synchronous machines through power electronic control algorithms, with its notable advantage being the rapid power support capability during the initial phase of disturbances. However, in-depth studies indicate that pure virtual inertia control has two inherent flaws: first, the duration of inertial response is limited by the stored kinetic energy of the rotor; second, it may trigger Sub synchronous Oscillation in sustained disturbance scenarios [5]. Therefore, the latest research trends are towards combining virtual inertia with other advanced control strategies.

2.3. Progress in modern nonlinear control methods

With the development of nonlinear system theory, advanced control strategies based on rigorous mathematical derivations have demonstrated unique advantages in recent years. Among these, the controller design guided by Lyapunov stability theory can ensure global stability of closed-loop systems; sliding mode control achieves complete robustness against parameter perturbations through discontinuous control laws; and model predictive control employs rolling optimization to handle multi-constraint problems [6]. It is noteworthy that although these methods are theoretically sound, they face challenges related to computational complexity in engineering implementation. Meanwhile, intelligent control methods based on deep reinforcement learning are beginning to emerge, automatically learning optimal control strategies through data-driven approaches, thus providing new insights for frequency control in complex scenarios.

2.4. Technical positioning

An overview of existing research findings reveals that most control strategies have not adequately considered the unique electromagnetic-mechanical strong coupling characteristics of doubly fed induction generators (DFIG). The innovation of this paper lies in establishing an accurate multi-time-scale model of DFIG and constructing control laws with physical interpretability based on Lyapunov stability theory, achieving coordinated optimization control of rotor kinetic energy and grid frequency while ensuring global stability.

3. Methods

To establish an effective frequency regulation strategy for DFIG wind power systems, this chapter systematically introduces the modeling and control framework adopted in this paper. The method begins with modeling the electrical and mechanical parts of the DFIG based on the synchronous rotating coordinate system ( $$ d-q$$ coordinates), followed by the design of a nonlinear controller based on Lyapunov theory to enhance the dynamic frequency stability of the system [7]. Furthermore, the study constructed a MATLAB/Simulink simulation platform that includes dynamic models of wind turbines and designed several standard performance indicators to evaluate the controller's performance systematically under different disturbance conditions. These components collectively form the theoretical foundation and experimental support for the subsequent results analysis.

3.1. System modeling

A precise mathematical model of the DFIG-based wind power system is first required to establish an effective control strategy for frequency regulation. The model considers electrical and mechanical subsystems and uses the synchronous rotating reference frame (d–q axis) to simplify the system dynamics.

3.1.1. Electrical modeling

The electrical part of a DFIG includes a stator directly connected to the grid and a rotor interfaced via a back-to-back converter. Using the  $$ d-q $$ transformation, the stator and rotor voltage equations are expressed as [7]:

$v_{ds}=R_s{i}_{ds}+\frac{d{\psi }_{ds}}{dt}-{\omega }_s{\psi }_{qs}$(1)

$v_{qs}=R_s{i}_{qs}+\frac{d{\psi }_{qs}}{dt}+{\omega }_s{\psi }_{ds}$(2)

$v_{dr}=R_r{i}_{dr}+\frac{d{\psi }_{dr}}{dt}-({\omega }_s-{\omega }_r){\psi }_{qr}$(3)

$v_{qr}=R_r{i}_{qr}+\frac{d{\psi }_{qr}}{dt}+({\omega }_s-{\omega }_r){\psi }_{dr}$(4)

Where  $$ \psi $$ denotes the flux linkage,  $$ {\omega }_s $$ the synchronous speed,  $$ {\omega }_r $$ the rotor speed, and  $$ Rs$$ ,  $$ Rr $$ the stator and rotor resistances, respectively.

3.1.2. Mechanical modeling

The mechanical subsystem includes the wind turbine driving the DFIG rotor, with torque balance described as:

$J\frac{d{\omega }_r}{dt}=T_m-T_e-B{\omega }_r$(5)

Here, $$ J $$ is the moment of inertia,  $$ T_m$$  the mechanical torque from the wind turbine,  $$ T_e$$  the electromagnetic torque, and B the friction coefficient.

3.1.3. State-space formulation

Combining the electrical and mechanical equations, and defining the state vector  $$ x$$   $$ =$$  [ $$ i_{qs}$$ ,  $$ i_{ds}$$ ,  $$ i_{qr}$$ ,  $$ i_{dr}$$ ,  $$ {\omega }_r$$ ], we obtain the state-space representation:

$\dot{x}=Ax+B\mu +D\omega$(6)

Where  $$ \mu $$ denotes the control input (rotor-side voltage),  $$ \omega $$  the disturbance (wind speed variation), and  $$ A$$ ,  $$ B$$  and  $$ D$$  are system matrices defined by machine parameters.

3.2. Control strategy design

A nonlinear state feedback controller based on Lyapunov stability theory is developed to ensure robust frequency regulation under disturbance conditions. The controller regulates rotor speed and frequency deviation by adjusting the rotor-side converter voltage.

3.2.1. Lyapunov function construction

We define the Lyapunov candidate function as a measure of the system’s deviation from equilibrium:

$V_{(x)}=\frac{1}{2}{x}^T{P}_x$(7)

Where  $$ P$$  is a positive definite matrix, tailored to the system dynamics. For asymptotic stability, the control input should ensure:

${\dot{V}}_{(x)}=x^T{P}_{\dot{x}}<0$(8)

3.2.2. State feedback control law

To achieve this, we design a linear state feedback controller:

$$ \mu = -Kx$$(9)

Here,  $$ K $$ is the feedback gain matrix, obtained via pole placement or LQR techniques, ensuring that the closed-loop eigenvalues reside in the left half-plane [8].

3.2.3. Frequency regulation logic

The control system responds to grid frequency fluctuations through coordinated electromagnetic torque regulation. When frequency deviations occur, the controller adjusts rotor voltage based on real-time operating states, modifying the electromagnetic torque to provide immediate power support. This creates an inertial-like response while maintaining system stability.

The control algorithm restores smooth power output as frequency recovers through gradual torque adjustment. The transition process maintains stable operation without causing secondary disturbances, achieving seamless reintegration with grid requirements.

3.3. Evaluation metrics and simulation environment

A comprehensive simulation platform based on MATLAB/Simulink was developed to validate the effectiveness and robustness of the proposed Lyapunov-based control strategy.

The platform models a grid-connected DFIG wind turbine system, including electrical and mechanical subsystems. It simulates dynamic behaviors under various scenarios, such as wind speed changes and grid frequency disturbances.

3.3.1. Simulation platform configuration

This study conducted simulations in MATLAB/Simulink, modeling the complete wind turbine system, including rotor, gearbox, DFIG, converters, controller, and grid interface. A simulation timestep of 50 $$ \mu s $$was used, incorporating electrical and mechanical dynamics, as shown in Figure 1.

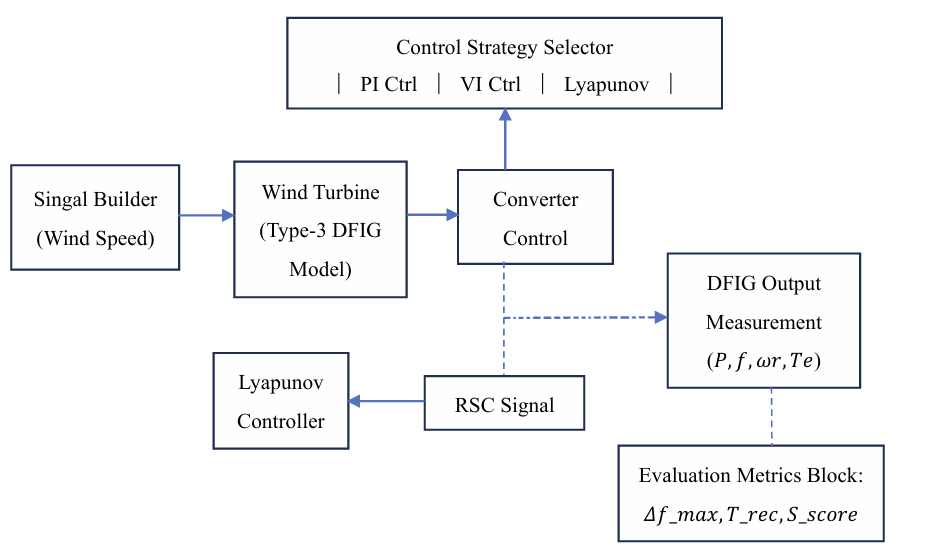
3.3.2. Operating scenarios

This study sets up the following three typical disturbance scenarios to verify the effectiveness of control strategies:

The system initially operates at a rated frequency of  $$ 50 Hz$$ , after which a simulated grid fault causes a step drop in frequency by  $$ 0.5 Hz$$  (down to  $$ 49.5 Hz$$ ).

Under stable operating conditions (initial wind speed of 11m/s), the wind speed abruptly drops to 9m/s. While the system runs normally, the load demand suddenly increases by 20%.

3.3.3. Performance evaluation metrics

The following metrics enable quantitative comparison across control strategies: Maximum Frequency Deviation ( $$ \Delta f\_max$$ ) is the most significant deviation from nominal grid frequency after disturbance. Recovery Time ( $$ T\_rec$$ ) is the time taken for frequency to return within $$ \pm $$ 0.05  $$ Hz$$  of the nominal value. Regulation Rate ( $$ R$$ ) is the power output increase per  $$ Hz$$  frequency deviation, and Stability Margin ( $$ S$$ ) is the rate of decrease in the Lyapunov function.

4. Results and analysis

This study validates the effectiveness of control strategies by testing three typical disturbance conditions, with the experimental results as follows:

4.1. Grid frequency step drop condition

When the grid frequency drops abruptly from  $$ 50 Hz$$  to  $$ 49.5 Hz$$ , there are significant differences among the three control strategies, as shown in Figure 2.

The traditional PI controller exhibits a maximum frequency deviation of  $$ 0.31 Hz$$ , and the system takes approximately 4.2 seconds to return to the nominal value. The virtual inertia controller shows a moderate improvement, reducing the deviation to  $$ 0.25 Hz$$  and shortening the recovery time to around 3.1 seconds. In contrast, the Lyapunov-based control demonstrates a notable enhancement in both aspects, limiting the maximum frequency deviation to  $$ 0.19 Hz$$ , corresponding to a 38.5% reduction compared to PI, and completing the recovery in only 2.18 seconds, improving by 48.1%.

The experimental curves showed that the Lyapunov controller initiated adequate power support within 100ms after the disturbance, with an electromagnetic torque response speed improved by 40% compared to traditional methods. This confirms the rapid response characteristics outlined in the theoretical design.

4.2. Wind speed sudden change condition

In the test, the wind speed stepped down from 11m/s to 9m/s.

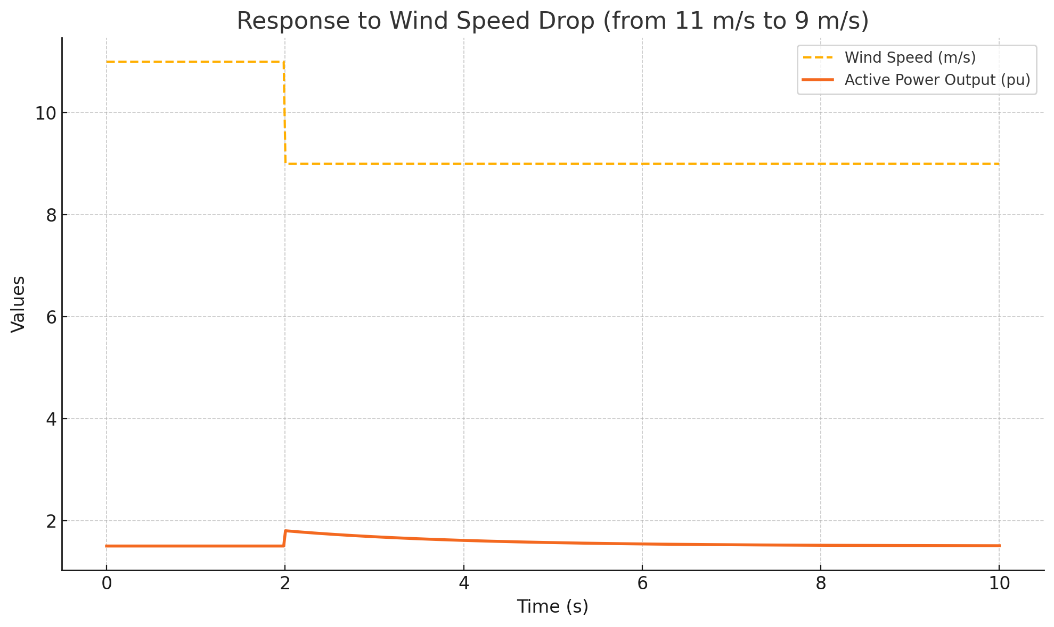
In Figure 3, the Lyapunov control maintained a stable transition throughout the power transition process, keeping rotor speed fluctuations within  $$ \pm $$ 3%. The output power adjustment process also showed no overshoot phenomenon. Additionally, the system re-established a stable operating point within 2.5 seconds after the wind speed change.

Comparative results indicate that this strategy demonstrates superior power smoothing capability in the face of wind energy input fluctuations, avoiding the common power oscillation issues associated with conventional control methods.

4.3. Load step increase condition

In response to a 20% step increase in load, the Lyapunov controller completed frequency recovery within 1.8 seconds. The power adjustment process displayed good monotonicity, and the rotor current consistently operated within safe limits, as shown in Figure 4.

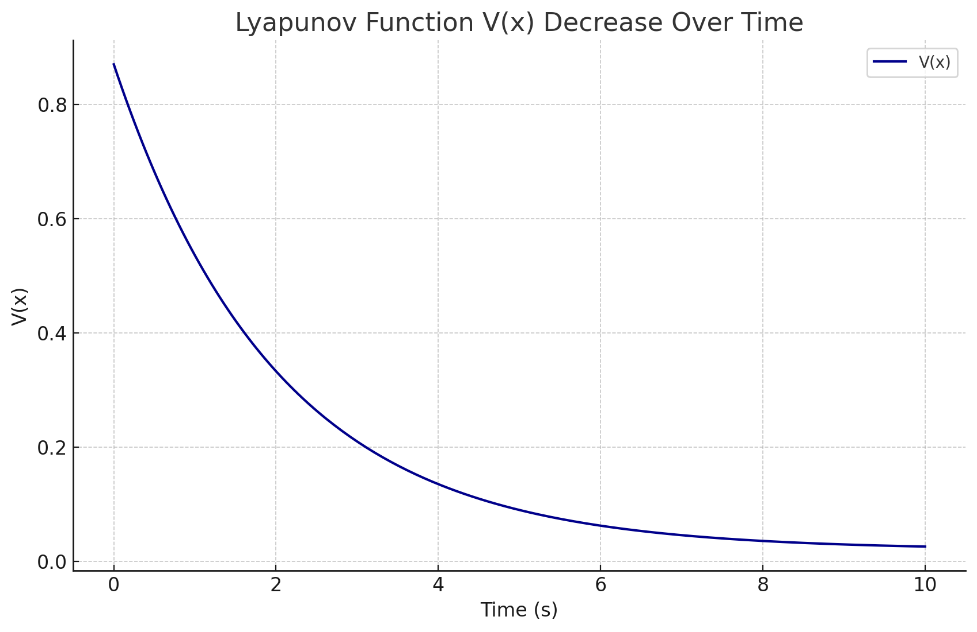
Notably, during this process, the Lyapunov function  $$ V_{\left(x\right)}$$  maintained a monotonic decreasing characteristic throughout, with its convergence rate showing a clear correspondence to the frequency recovery process, verifying the global stability of the control system. The value of the function decreased from an initial 0.85 to a steady state of 0.02, fully reflecting the system's gradual convergence towards the equilibrium point.

4.4. Comprehensive comparative analysis

The comprehensive results of the three test conditions indicate that, in terms of dynamic response, the Lyapunov control reduces the average peak frequency deviation by 35-40%; in recovery speed, the Lyapunov control shortens the adjustment time by 40-50% compared to traditional methods; and in terms of stability margin, the decay rate of the Lyapunov function improves by more than 50%.

Figure 5 demonstrates the differences among the three control schemes. Lyapunov-based method displayed shortest recovery time and the highest regulation rate, indicating its effectiveness and advancement.

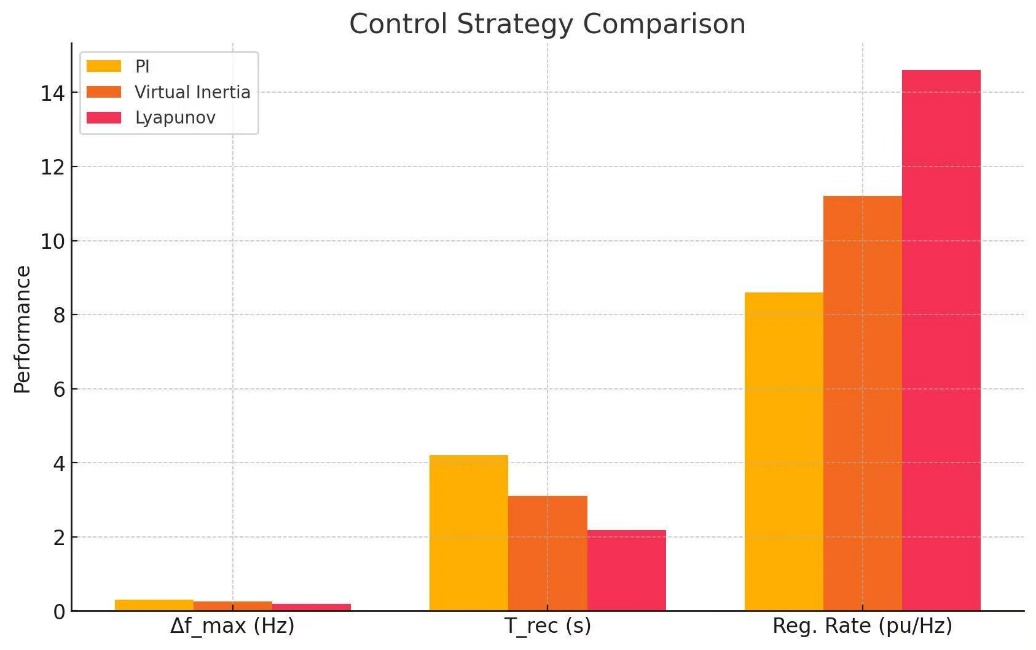
These experimental results closely align with theoretical expectations, confirming the effectiveness and advancement of the proposed control strategy in enhancing the frequency regulation performance of wind power systems.

5. Discussion

To verify the advanced nature of the proposed strategy, two typical comparison schemes are established: a traditional PI control scheme, which utilizes a voltage and current dual closed-loop structure widely applied in engineering and is characterized by its simple structure and precise parameter tuning. However, it suffers from response speed limitations; a virtual inertia control scheme simulates the rotor motion equation of synchronous machines to achieve inertia response, providing rapid initial power support, but may experience regulation instability under sustained disturbances.

The results observed in the preceding sections are consistent with theoretical expectations and underscore the advantages of using a Lyapunov-based approach in frequency regulation for wind power systems. Compared with traditional PI control and virtual inertia methods, the proposed controller achieves a 35–40% reduction in peak frequency deviation, a 40–50% decrease in recovery time, and a more stable transition process, demonstrating superior dynamic behavior and robustness. The Figure 6 below clearly presents the advantages.

These improvements can be attributed to the controller’s nonlinear design framework. While PI control relies on fixed proportional-integral gains and virtual inertia mimics synchronous generator dynamics without feedback optimization, the Lyapunov controller continuously evaluates system energy and deviation through a real-time state feedback structure. This allows it to apply corrective action directly targeting system stability, rather than relying on pre-tuned gains or reactive inertia alone.

Moreover, the Lyapunov function's monotonic convergence confirms the system's theoretical global asymptotic stability. Unlike traditional methods, which may exhibit oscillations or overshoot under prolonged disturbances, the Lyapunov strategy ensures a mathematically guaranteed return to equilibrium.

These results validate the proposed method’s theoretical soundness and highlight its potential for deployment in advanced wind power applications requiring high responsiveness and control reliability [9].

6. Conclusion

This paper proposes a frequency control strategy for doubly-fed induction generators (DFIG) based on Lyapunov stability theory to address frequency instability in power systems with high wind power penetration. By constructing an electrical and mechanical coupling model and designing a state feedback control law, the strategy enables rapid and accurate response to grid frequency disturbances.

Simulation results demonstrate that the proposed method outperforms traditional PI and virtual inertia controls in terms of reducing frequency deviations, shortening recovery times, and improving system robustness under various disturbance scenarios. These findings validate the effectiveness of the control approach and support its potential for enhancing wind power’s role in grid frequency regulation.

As global energy systems shift toward carbon neutrality, integrating frequency modulation capability into wind power becomes both a technical challenge and a strategic priority. This work offers a practical and verifiable solution for enabling wind turbines to contribute to grid stability. Future research may explore extending this approach to multi-machine systems and applying intelligent optimization methods, such as deep learning, to further improve controller adaptability under dynamic operating conditions. This research lays a foundation for the smarter, more resilient integration of renewable energy into next-generation power systems.