1. Introduction

Analog Integrated Circuit (IC) design contains billions of nanoscale transistors, which is important while dealing with signal processing and connecting the physical analog world with digital information [1]. However, in terms of the analog IC design, the parameters of the analog IC design strongly reply to the judgment of the researchers and designers themselves. Also, the entire process of the design is time-consuming and inefficient.

According to previous studies, the automation of analog circuits can be basically classified into two categories: knowledge-based and optimization-based approaches [2]. In implementing knowledge-based approaches, algorithms and equations are generated based on the experts’ understanding of their domain knowledge. Therefore, these algorithms and equations are very dependent on the experts themselves, the structure of the circuit and the technical nodes [3-4]. Under most circumstances, experts will adapt optimization-based methods. Figure 1 demonstrates the conventional process of machine learning-based design [5]. It can be seen that optimization-based algorithms and equations can be applied to machine learning. With machine learning, the process can be effectively automated, thus reducing the time required and providing efficiency.

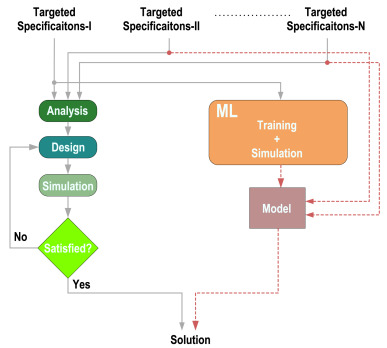
Figure 1 The process of the ML-based Design [5]

Over the past few years, a great deal of research has existed regarding the use of machine learning to improve the efficiency of automation of analog integrated circuits. Many classifications of methods have been mentioned in these studies, where these techniques can be classified as supervised learning and unsupervised learning.

2. Machine Learning

2.1. Supervised learning

As for supervised learning, it is necessary for the training data to include the desired solution, which is named a label [5]. For the regression problem, the label will be continuous-valued. In terms of the classification problems, it will be categorical[5]. The algorithms concerning supervised learning can be broadly summarized as follows: linear regression, logistic regression, decision trees, naïve bayes etc.

2.1.1 Multiple Linear Regression (MLR). The form of the linear regression will be shown below:

\( y=a+{b_{1}}x+{b_{2}}x+…+{b_{n}}x+c \) (1)

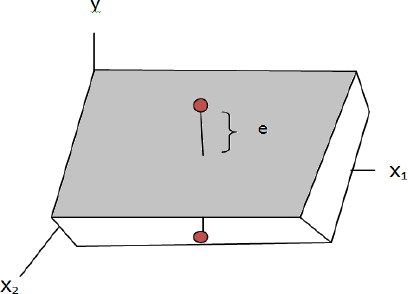
Where, y is the dependent variable, x is the independent variable, and \( {b_{n}} \) is the parameter. Figure 2 shows the model of the 3D MLR [6].

Figure 2 3D MLR Model [6]

The MLR can be seen as an extension of the simple linear regression. It contains more than one independent variable. Therefore, since there are multiple independent variables, the results using this algorithm can be more precisely associated with each individual variable. In a practical application of supervised learning, experts first use training data to train a model to make it more accurate and then apply the model to testing data to check its accuracy of the model.

\( P(Y=1)=\frac{exp⁡(α+\sum {β_{i}}{X_{i}})}{1+exp⁡(α+\sum {β_{i}}{X_{i}})} \) (2)

Logistic regression applies data to a logistic function to predict the probability of an event occurring. Figure 3 shows the difference between the linear and logistic functions. Both of these regression methods are used to estimate the relationship between the dependent and independent variables. However, linear regression produces a continuous output, while logistic regression produces a discrete output.

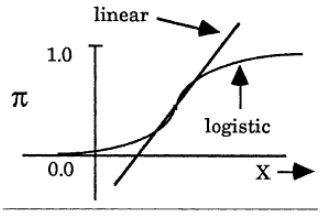
Figure 3 The presentation of Linear and Logistic functions of X [7]

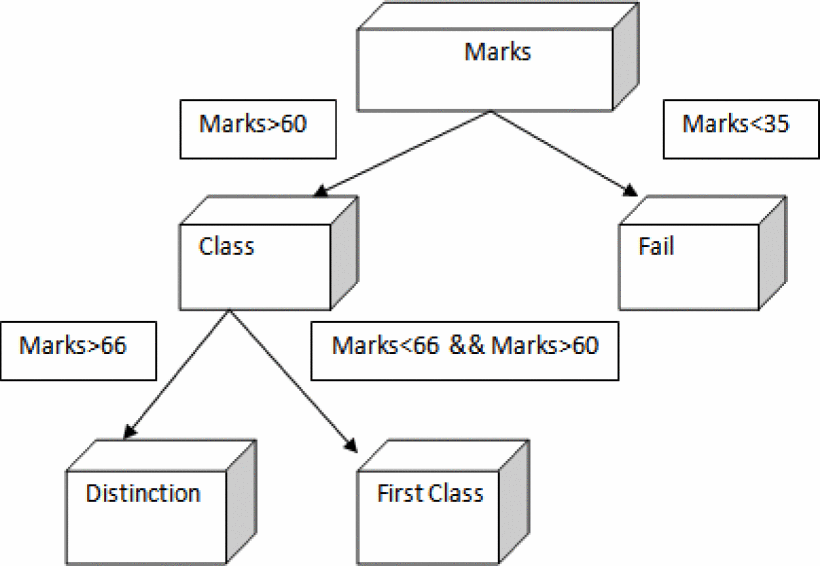
2.1.2 Decision Trees [8]. Decision trees can sort through a large amount of input data, and the advantage of this method is that it can handle data that contains missing values or numerical errors. Figure 4 is an example of a decision tree that briefly describes how to classify, store, and reclassify when using a decision tree.

There are four main algorithms of decision trees:

C4.5: Use the information gain ratio to classify the data.

Cart: The algorithm is a binary algorithm that incorporates classification and regression.

Chaid: This algorithm is used to find the minimum difference pair of values in the attributes.

ID3: This algorithm is used in conjunction with C4.5, which also uses information gain to classify the attributes of the data. This algorithm is not applicable to any pruning.

Figure 4 Example of Decision Tree [8]

2.1.3 Naïve Bayes. The Bayesian classification is a classified statistical method, which provides fast, highly scalable training. The advantage of this classification is that does not need a large training set.

There are two values with general probability distribution [9]. The equation will be given by applying the Bayes rule.

\( P({X_{1}},{X_{2}})=P({X_{1}}|{X_{2}})P({X_{2}}) \) (3)

A second equation will be generated with more class variable c [9].

\( P({X_{1}},{X_{2}}|C)=P({X_{1}}|{X_{2}},C)P({X_{2}}|C) \) (4)

By generalizing the second situation, the equation below will be given [9]:

\( P(X|C)=\prod _{i=1}^{N}P({X_{i}}|C) \) (5)

2.2. Unsupervised learning:

Unsupervised learning is the use of machine learning algorithms to give analysis and aggregation to unlabeled data sets. This type of algorithm does not require human intervention.

2.2.1 Clustering. Clustering is also the process of classifying objects with similar attributes. It groups unlabeled sets of data into predefined clusters and looks for structure. The methods of data clustering can be classified as hierarchical or partial.

3. Analog IC Design with Machine Learning

3.1. Supervised Learning with Analog Integrated Circuit Design

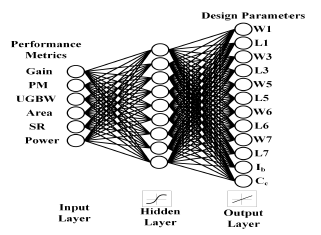
3.1.1 Artificial Neural Networks Model (ANNs)[10]: The expert's design for the method can be divided into two parts. The first part is about the generation of the dataset. In terms of the input parameters, there are six items considered: Gain, Phase Margin, Unity Gain Bandwidth, Area, Slew Rate(SR) and Power. And twelve design parameters as output: {W1, L1, W3, L3, W5, L5, W6, L6, W7, L7, , }. In this approach, the experts have adopted a special software framework to generate the dataset called MaxFit Genetic Algorithm-SPICE. The framework is a genetic multi-objective optimization algorithm based on a genetic multi-objective optimization algorithm that relies on a set of already predefined circuit equations that the designer of the analog circuit has developed [11]. Figure 5 shows the network structure of this ANN model, from which it can be seen that there are many hidden layers as well as a multilayer perceptron of neurons to map the input-output relationship. For the process of training, they use Bayesian regularisation back-propagation algorithm to reduce the error. The number of hidden layers in each hidden layer of the amplifier is combined with different neurons. After the model of the analog IC circuit is generated, a new set of feature data will be used to test the accuracy of the model, and the results will be compared with SPICE.

Figure 5 ANN Structure [10]

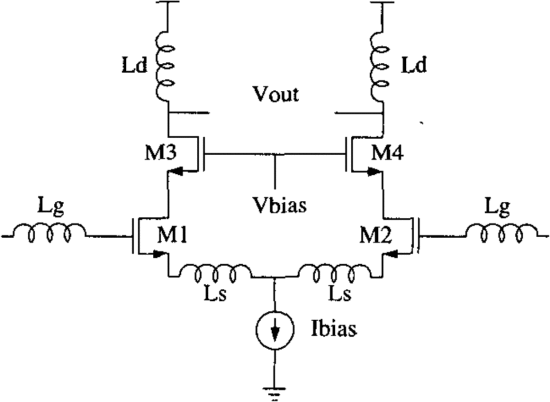
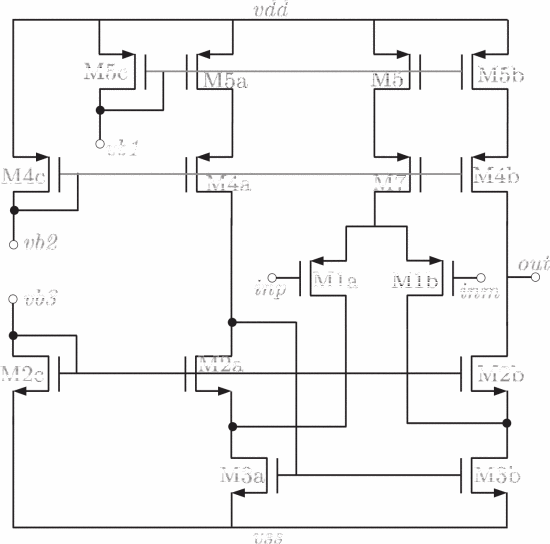
3.1.2 Support Vector Machines Model [12]: Support Vector Machines (SVMs), an algorithm for supervised learning, can also be used to represent the performance of the analog integrated circuit. Throughout the process, as with traditional supervised learning, a set of input parameters will be mapped to a set of performance arrays via an analog circuit. Experts quantify the data that may be required, one of the more difficult to solve is performance relation. In this particular approach, experts have proposed two methods to perform the estimation of data. Figure 6 shows the basic schematic of a low noise amplifier that will be used in this model.

Two-class SVM[12]: two Class SVM will allow the approximation to form a separate discriminant boundary from its complementary part. Experts have developed three different heuristics that will be used to specify the appropriate density function.

One-class SVM [12]: the one class SVM requires only one class of data as a sample and is implemented by solving a quadratic optimization problem. The formula will be shown as below:

\( \underset{w, ξ,ρ}{min}{\lbrace \frac{1}{2}||w|{|^{2}}+\frac{1}{vm}\sum _{i}{ξ_{i}}-ρ\rbrace } \) (6)

The accuracy of the estimator can be determined by the expansion of conformal transformation.

Figure 6 Schematic of the Low Noise Amplifier model [12]

3.1.3 Regression Algorithms in Analog Circuit Design [13]: The main purpose of this approach is to apply regression models to reduce the time to simulate circuit performance. The most central technique in the complete process is the variant of the Gaussian Processes (GPs) model. After studying the variants of the Gaussian process, the experts proposed nine regression algorithms: GP Scikit, GP Rasumussen, GPLP Park, spGP (Ed Snelson), KRG, KRC, pyXGPR (Neumann), FFX, RIWD. Figure 7 shows the circuit diagram that was used for testing. In this experiment, 13 design parameters based on the currents and voltages on each side of the transistors are input. The results of the experiments show that only FFX and spGP can implement the medium and high dimensional problems.

FFX: A symbolic regression which can discover the difference regression coefficients by Pathwise Regularized Learning [14].

spGP: One way of regressing Gaussian processes by using gradient-based optimization [15].

Figure 7 Schematic of High Voltage Model [13]

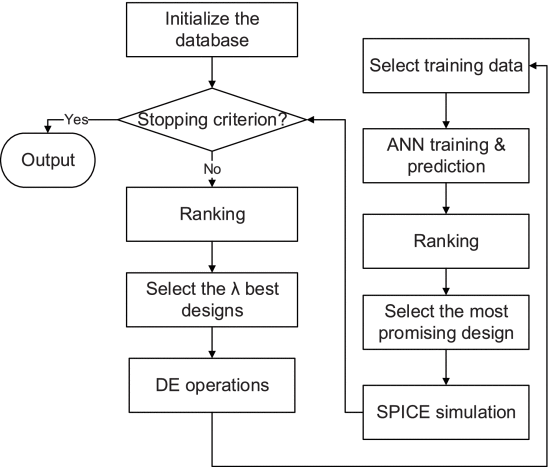
3.1.4 Machine learning-assisted global optimization methods[16]: this method is a combination of ANNs model and candidate design ranking method. The researchers called it efficient surrogate model-assisted sizing method for high-performance analog building blocks (ESSAB)[16]. Figure 8 shows the basic step about the ESSAB model.

Figure 8 Flow Chart of the ESSAB [16]

The first Ranking [16]: The results of the new infill sampling criterion will be used in the ranking process.

ANN Training & Prediction [16]: The distance between ANN predictions and simulated values is calculated using a loss function to train the weights with two layers that are hidden. ANN(x+∆x) is the prediction value of ANN, and y(x+∆x) is the performance given by simulations.

3.2. Comparison

Both the ANNs model and the SVMs model are more suitable for learning with small samples. The SVMs model can better solve the structural instability than the other two methods mentioned above, especially the ANNs. The ANNs mentioned above will apply some already predefined circuit equations that the designer of the analog circuit has developed, and the uncertainty of such empirically based equations is likely to affect the accuracy of the final results. SVMs model, however, employs deterministic subtypes and therefore has higher stability. Also, compared to ANNs models, SVMs are less susceptible to local minima.

The use of the regression algorithm in analog circuits is, on the other hand, the simplicity of its use. It is mentioned in [17] that in the determination of the parameters of the analog circuit, the regression algorithm can better create accurate modules, thus improving the accuracy of the analog system. However, when applying regression models to save simulation time, experimental results [13] show that for problems of medium size, the prediction error will increase when more construction time is invested. However, for high-dimensional problems, it may lead to problems such as convergence failure. Overly large datasets make the used methods change their performance, thus generating failure cases.

The last method mentioned above, Machine learning-assisted global optimization methods, can be seen as an extended deformation of the first method. It is more stable than the traditional ANNs model and takes less time to finalize than the ANNs model. However, this approach may require more parts (amplifiers and operators) to implement for SVMs, and it is possible that it will cost more than the SVMs model. However, due to the lack of cross-sectional comparison, it is not possible to determine which is more efficient, the SVMs model or the Machine learning-assisted global optimization methods.

4. Conclusion

According to the various algorithms of machine learning listed above and the use of machine learning in the simulation of integrated circuits, it can be found that the model of SVMs has more stability as well as excellent generalization ability compared to the other two models. Therefore, researchers prefer to use SVMs models when optimizing analog integrated circuits. The automation of analog IC design can effectively reduce the impact of the surrounding environment on the data while greatly improving the efficiency of optimization. However, in these studies, it can be found that both ANNs and SVMs models and regression algorithms are more suitable for small and medium-sized datasets. For large datasets, there are problems associated with the use of the models, which may even cause case failure.

Future developments in the use of machine learning on analog integrated circuits should focus more on the size of the data set and the complexity of the circuit. Also, the three approaches provided above can be appropriately deformed to be applied to other aspects, e.g., finding performance space representations.