1. Introduction

Thermonuclear fusion is the reaction of light nuclei into a heavier nucleus by a collision of the interacting particles at extremely high temperature, which release of a large amount of energy due to the mass defect. The general expression is \( E=Δm{c^{2}} \) , where \( E \) is the released energy, \( Δm \) is the mass defect, and \( c \) is speed of light. Extremely high temperature and pressure are the necessary conditions of fusion. For example, the deuterium-tritium (D-T) fusion reaction occurs at temperature in excess of 175 million degrees Celsius and that of deuterium-deuterium (D-D) at approximately 232 million degrees Celsius. One of promising ways to heat fusion fuel is by laser pulse. In 2022, US National Ignition Facility (NIF) used 192 lasers to heat a bean-sized gold cylinder which containing deuterium and tritium. Engineers used 2.05 megajoules of laser energy which caused deuterium and tritium fused into helium and released energy to support further fusion reactions. Facility announced that the reaction released more than 3.15 megajoules which more than 50% of energy put into the reaction [1]. Although the reactor is collapsed because of extremely high temperature, this is the first time that reactor can release energy more than laser’s energy.

Nuclear fusion can produce a large amount of clear energy. However, controllable fusion reaction is a technical problem. The biggest challenge is designing a reactor cannot be collapsed by extremely high temperature and reactor can control fusion reaction. Since first successful man-made fusion device is over 70 years, it is highly desirable to review the current progress. To this end, this paper will discuss two typical models of reactor, together with their manner of working and challenges. In Section 2, detailed thermonuclear fusion is discussed. Next, paper describes fusion reactor in Section 3. Finally, Section 4 is devoted to the conclusion of properties of fusion reactor.

2. Thermonuclear fusion

2.1. Coulomb barrier

Nuclear fusion occurs when two light nuclei close enough. However, by Coulomb repulsion, two nuclei need to overcome the Coulomb potential, which is given by

\( {E_{C}}=\frac{1}{4π{ϵ_{o}}}\frac{{Z_{1}}{Z_{2}}{e^{2}}}{R}\ \ \ \) (1)

where \( {Z_{1}} \) and \( {Z_{2}} \) are the atomic number of two nuclei and \( R \) is the distance of closest approach. Therefore, people used to increase the thermal energy of two nuclei to overcome the Coulomb barrier by heating them. The thermal energy is given by

\( {E_{t}}=\frac{3}{2}{k_{b}}T\ \ \ \) (2)

where \( {k_{b}} \) is Boltzmann constant and \( T \) is the temperature. The temperature for a Deuterium-Tritium fusion (D-T fusion) calculated is \( 4.5×{10^{7}}K \) [2].

In Stellar fusion, the required temperature is larger than temperature of stellar interior which means stellar is not hot enough to support D-T fusion. This is why many scientists refused to accept fusion occurred in the Sun when the expression was made at first time. In the fact, fusion did occur in stellar because of two reasons. The major one is quantum tunnelling, which means nuclei doesn’t need have estimate energy to overcome the Coulomb barrier. Another reason is there is a small number of nuclei which have more than estimate energy. According to Maxwellian distribution of energy, the thermal energy of nuclei is the mean energy so some of nuclei have higher energy than mean energy which is possible to exceed the estimate energy.

2.2. Stellar fusion

There are many fusion cycles occur in stellar. The most famous cycle is proton-proton fusion cycle (PP) suggested by Gamov and Weizsacker in 1937 and developed by Bethe in1939. PP cycle is majority fusion occurs in the Sun and lower-mass stellar. Carbon-nitrogen-oxygen cycle (CNO cycle) is main source of energy in stellar heavier than the Sun.

For the PP cycle, it starts with the two protons to fuse deuterium by the weak interaction

\( p+p{→ ^{2}}H+{e^{+}}+{ν_{e}}\ \ \ \) (3)

where \( {e^{+}} \) is positron and \( {ν_{e}} \) is electron neutrino. The positron will annihilate with electrons in the plasma, the net reaction called PEP reaction.

\( p+p+{e^{-}}{→ ^{2}}H+{ν_{e}}\ \ \ \) (4)

The deuterium fuses one more proton to produce

\( p{+ ^{2}}H{→ ^{3}}He+γ\ \ \ \) (5)

The will fuse with other nuclei to produce more heavier nuclei, the majority of fusion called pp-I

\( +{→ ^{4}}He+2p\ \ \ \) (6)

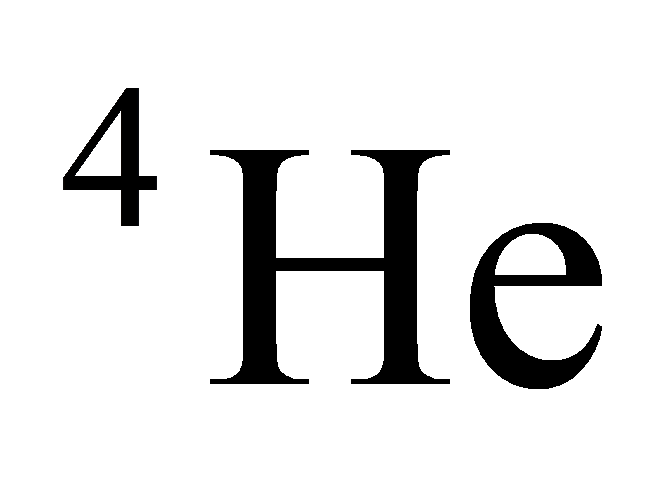About \( 2×{10^{-5}}\% \) of fusion \( (hep-ν) \) is \( p{+ ^{3}}He{→ ^{4}}He+{e^{+}}+{ν_{e}} \) . Some of will fuse with to produce 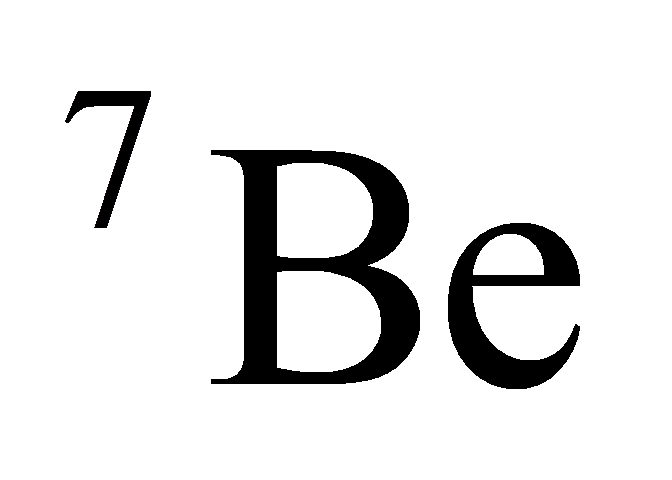\( {: ^{3}}He{+ ^{4}}He{→ ^{7}}Be +γ \) . pp-II and pp-III are further reactions, majorly reactions of pp-II are

\( {e^{-}}{+ ^{7}}Be{→ ^{7}}He+{ν_{e}}, +p→{2^{ 4}}He\ \ \ \) (7)

pp-III are

\( p {+ ^{7}}Be{→ ^{8}}B+γ, {→ ^{8}}B{e^{*}}+{ν_{e}} +{e^{+}}, →{2^{ 4}}He\ \ \ \) (8)

Here, is an excited state of beryllium. Protons fused into helium () and release energy because of the mass defect. This is how stellar produce energy [3].

Unlike PP cycle, CNO cycle starts heavier element which produced by triple- alpha process which three alpha particles are fused into carbon

\( +→,+{→ ^{12}}{C^{*}}+2γ\ \ \ \) (9)

where 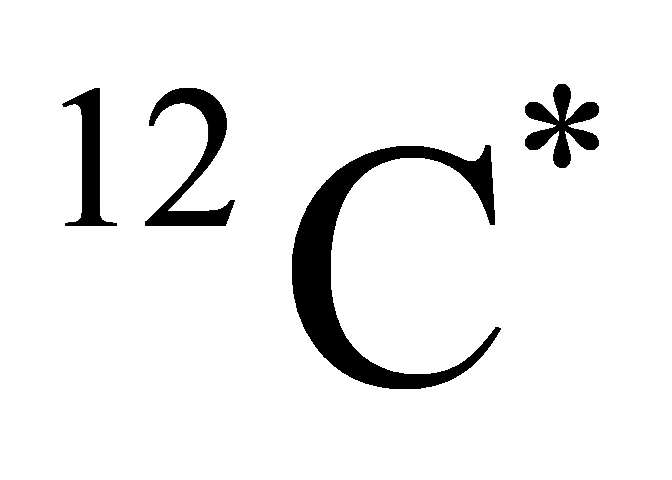is an excited state of carbon. The major reaction is called CNO-I: \( p+{→ ^{13}}N+ γ \) . The will proceed beta-decay \( :→ { ^{13}}C+{e^{+}}+{ν_{e}} \) . The further CNO-I functions \( p+→γ + \) , \( p +→+γ, →+{e^{+}} {ν_{e}} \) , and \( p + → + \) .

2.3. Deuterium-deuterium and Deuterium-tritium fusions

Stellar produce energy by PP fusions; however, PP fusions are slow to reaction because of quantum tunnelling. The sun produces a large amount of energy because the volume of the sun is extremely huge. Nowadays, scientists use deuterium and tritium to fuse heavier nucleus.

\( {+^{2}}H→+n, {+^{2}}H→ +p, {+^{3}}H→+n\ \ \ \) (10)

Although D-D fusion and D-T fusion have same Coulomb potential as PP fusion, D-D fusion and D-T fusion can release more energy because of more mass defect.

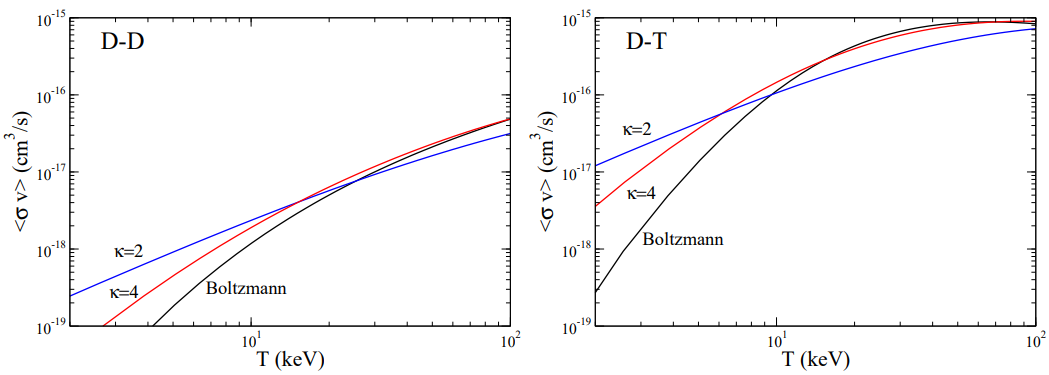
Figure 1. The reactivities of D-D and D-T fusion with three types of energy distribution, the Boltzmann energy distributions (black) and two \( κ \) -distributed energy, \( κ=2 \) (blue) and \( κ=4 \) (red), in 2-100 keV temperature range. \( ⟨σv⟩ \) is reactivity and \( T \) is temperature [4].

In Figure 1, D-T fusion has much higher cross-section which means the possibility of reaction is higher than D-D fusion over same temperature. With \( κ \) -distribution, D-T fusion at relatively low temperature, the reactivity gains of two orders of magnitude compare with the Boltzmann energy distributions [4]. In fact, \( κ \) -distribution provide a straightforward replacement of the Maxwell distribution for systems out of the thermal equilibrium such as space plasmas [5]. Comparing D-D and D-T fusion, D-D fusion requires higher temperature to achieve a great rate, but tritium is not common in natural compare with deuterium. Both reactions have the advantage and the disadvantage, scientist tends to use tritium as nuclear fuel because of development of tritium-breeding. Modern D-T reactors have special layers of material which can produce tritium upon neutron bombardment which is produced by D-T fusion [6].

3. Fusion reactor

Fusion reactor subjects to many limitations, how to simulate stellar is a challenge. Stellar has huge size and release lager mount of energy, even though the rate at which energy released is low. Scientists have to design a reactor which is more efficient. At present, fusion reactor uses D-T fusion instead of PP fusion. There are two typical models of reactor, magnetic confinement and inertial confinement.

3.1. Inertial confinement fusion

Inertial confinement fusion (ICF) uses inertial confinement reactor model. There are two ways to heat the capsule, direct drive and indirect drive. In direct drive, the laser drive to the capsule directly. The laser mast be symmetric to heat fuel because of Rayleigh Taylor instability, so the capsule and the laser have size limit. In indirect drive, scientists use laser energy which is converted to X-ray drive to implode a capsule of D-T fuel covered by an ablator. The function occurs in a hohlraum which has laser entrance holes (LEH) at either end [7], as shown in figure 2. Comparing two ways of heating, direct drive has more energy efficient because the laser energy onto the capsule directly and the laser energy lose due to preheating in indirect drive. On the other hand, direct drive is hard to achieve due to many limitations. Through the hohlraum, laser can be less accurate to heat fuel uniformly.

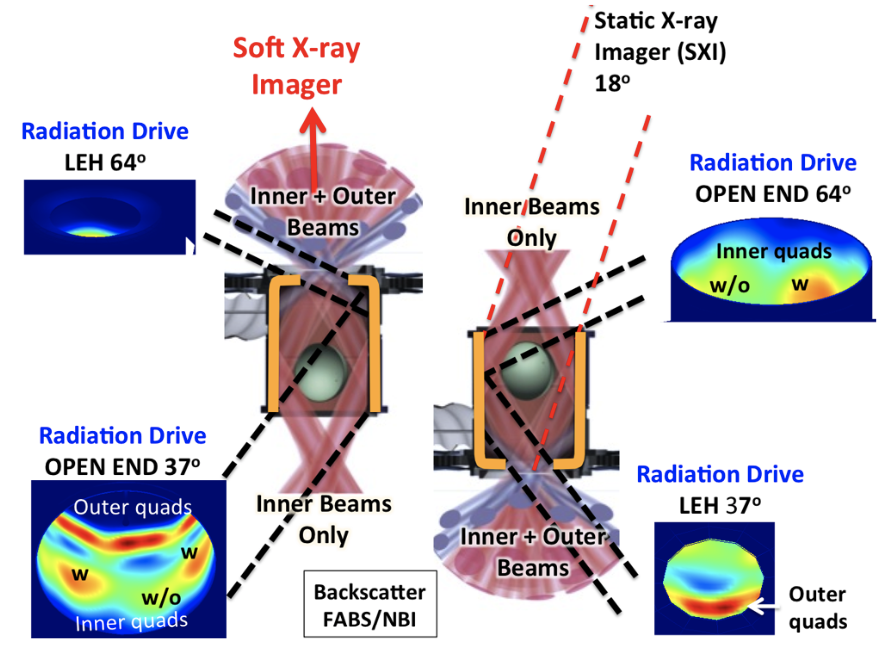
Figure 2. The diagram of hohlraum [7].

The goal of the NIF is increase the release energy “yield” in ICF higher than the ignition threshold and input energy. Though the experiment, scientists focus on increasing the capsule size to absorb more energy and decreasing the hohlraum size to decrease wall losses [8]. Primary challenge is how to maintain the continuation of the reaction and output energy should be more than input.

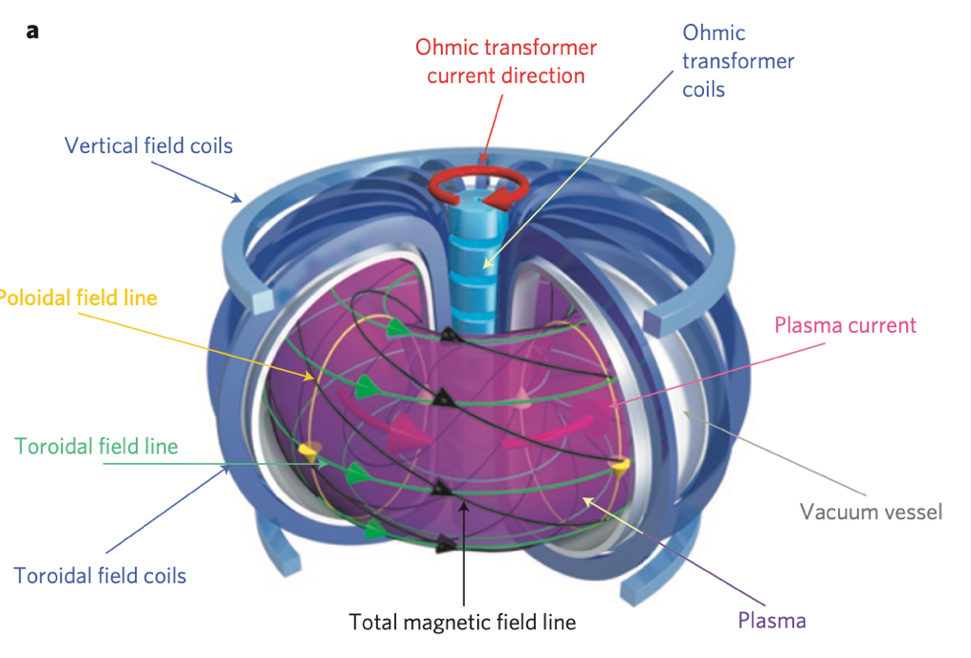
Figure 3. The diagram of toroidal tokamak, plasma particles are confined while them move around in vacuum vessel [9].

3.2. Tokamak

Tokamak is magnetic confinement fusion reactor, and it has some advantages. Fusion occurs at extremely high temperature, and fusion fuel has plasma property under this condition. Tokamak uses magnetic field to confine plasma. A straight cylinder magnetic field can trap plasma, but some plasma particles can escape. The escaped particles can be reduced by adding two stronger magnetic field at both ends, stronger force at ends causes plasma reverse direction and return to confinement area; however, plasma still can escape if they move along the magnetic field lane. A toroidal shape of tokamak is another way to solve this problem. The toroidal vacuum vessel is around by a toroidal magnetic field which is produced by toroidal coils [9], see figure 3.

A neutron is created in D-T fusion and neutron is move free in the vessel because it does not have charge. Neutron will hit the wall and increase temperature; the wall is called blanket system which can absorb neutronic heating to boil water to supply generator to create electricity.

3.3. Challenge

ICF is a promising way to achieve continues ignition, but we cannot transfer the nuclear energy to an effective and safe energy because ICF acts more like a nuclear weapon. On the other side, laser is another challenge. Due to low efficiency of laser, larger power laser is necessary condition, which will increase the input energy. The consequences are output energy must increase because output energy must larger than breakeven point. More energy may cause safety problem, reactor collapse and nuclear fusion out of control.

Tokamak also has some major challenges. We need to inject deuterium and tritium continuously to maintain the reaction, but it will decrease the temperature which can cause reactivity decreasing. Because of the neutron irradiation, the blanket system will be deteriorated which may cause safety problem and increased difficulty in repairing. Strength of magnetic field is a nonnegligible problem. In 2002, one attempt of 0.6 T magnetic field caused breakdown and arcing in the upper contact joint of the toroidal field coil [10]. The reason tokamak needs stronger magnetic field is reduce plasma leak and reduce the size of the reactor.

4. Conclusion

With the development of technology, many technical problems have been solved. ICF use laser to heat fuel efficiently, through increasing the capsule size and decreasing the hohlraum size to achieve increasing yield. Tokamak use magnetic field to confine 150 million °C plasma to fuse. With the \( κ \) - distribution, allow to increase the number of energetic deuterium and tritium to fuse which reactor can have lower temperature. Both of reactor have advantages; however, many technical problems have to solve to achieve controllable nuclear fusion. In the future, tritium-breeding can solve nuclear fuel scarcity because tritium is scarce in nature. Superconductor may create stronger magnetic field to support tokamak because tokamak needs stronger magnetic to trap the plasma. The reason why we need fusion reactor because a controllable fusion reactor can provide almost unlimited energy and can solve the energy crisis.