1. Introduction

In the modern automotive industry, improving engine efficiency has become an important issue due to its significant impact on vehicle performance, fuel consumption, and emissions. Four-stroke and two-stroke engine technologies are the two main types of internal combustion engines used in vehicles. However, there is still a debate over which type of engine is more efficient and suitable for different applications.

Therefore, the purpose of this study is to compare the engine efficiency of four-stroke and two-stroke engines. Specifically, The following are the questions that will hopefully be answered by this study:

1) How do two-stroke and four-stroke engines differ in terms of thermal efficiency, braking power, and specific fuel consumption?

2) Which type of engine is more efficient in terms of these parameters?

3) What are the implications of the findings for the choice of engine in different applications?

To achieve these objectives, a sample of engines, including both four-stroke and two-stroke engines, will be evaluated based on the aforementioned parameters. The results of the study will be analyzed and compared to determine the differences in engine efficiency between the two types of engines.

This study is expected to contribute to the understanding of the engine efficiency of four-stroke and two-stroke engines and provide valuable information for the selection of engines based on specific application requirements.

2. Gasoline engine: Otto cycle with Van der Waals gas as working fluid

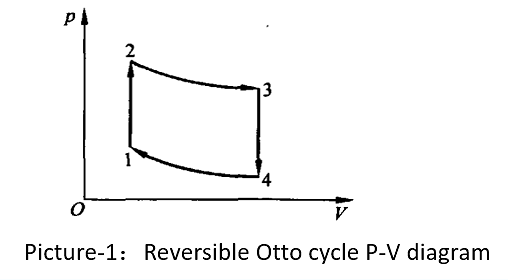
Figure 1. Reversible Otto cycle P-V diagram [1].

It is assumed in Figure 1 that 1 mol of Van der Waals gas travels through a reversible Otto cycle 12341 when used as the working medium in an Otto cycle. The processes in (1) are isothermal endothermic, (2) are adiabatic expansions, (3) are isothermal exothermic, and (4) are adiabatic compressions. V1 and V2 are the minimum and maximum volumes in the cycle respectively [2]. One mole of a real gas, according to the Van der Waals equation:

\( (p+\frac{a}{{V^{2}}})(V-b)=RT \) (1)

\( dQ=C_{V}^{1}dT+\frac{RT}{V-b}dV \) (2)

\( T{(V-b)^{\frac{R}{C_{V}^{1}}}}=C \) [1](3)

Heat engine efficiency is defined as \( 1-\frac{{Q_{34}}}{{Q_{12}}} \) , but now, we are talking about van der Waals gas, in this formula, P equals pressure, V equals volume, an equal’s Intermolecular attraction, b equals Volume occupied by molecules, T equals temperature, R equals to a constant — 8.31. So we should use formulas eight and ten. Formula eight is talking about Heat change in the isovolumetric process, formula ten is talking about the formula of the adiabatic process. After a series of operations, we can conclude that efficiency equals the r divided bided by volume one. γ equals free plus two divided by free. Gasoline engines have compression ratios of 4 to 6, so we can figure out that the ideal efficiency is 40% to 60%. But in fact, efficiency is just 30%－40%. It is a result of the exhaust loss. Exhaust loss refers to the cycle work loss from the exhaust valve opening in advance until the intake stroke starts and the pressure in the cylinder reaches atmospheric pressure [2][3].

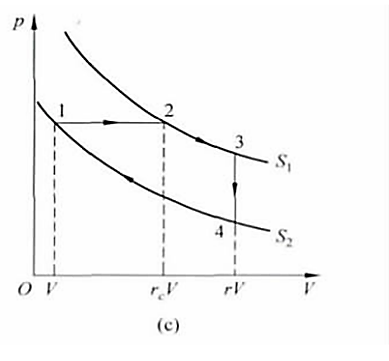
Figure 2. Reversible diesel cycle P-V diagram [1].

3. Diesel engine: diesel cycle with van der Waals gas as working fluid

Diesel engines employ the thermodynamic Diesel cycle. The Diesel cycle burns fuel by injecting it into the combustion chamber and compressing the gas. The Otto cycle in a four-stroke engine utilizes a spark plug to ignite the fuel-air combination in the combustion chamber, whereas the diesel cycle does not [4][5]. 2-3 and 4-1 are adiabatic, 1-2 and 3-4 are isobaric. Isobaric process 1-2 is endothermic, isobaric. 3-4 is exothermic, T1234 is the temperature at 1234 places in the diagram, as (28) equation, \( k=\frac{b}{V} \) , \( {a_{r}}= \frac{a}{R{T_{1V}}} \) , \( {T_{2}}({V_{2}}-b)γ-1={T_{3}}({V_{3}}-b)γ-1={T_{3}}({V_{3}}-b)γ-1 \) ; \( {T_{4}}({V_{4}}-b)γ-1={T_{1}}({V_{1}}-b)γ-1 \) , assumed \( {T_{1}}=300K, {T_{2}}=800K \) , so we can figure out that efficiency is about 35%－43% [1].

\( η=1-\frac{({T_{3}}-{T_{4}})}{{({T_{2}}-{T_{1}})+(γ-1)({T_{2}}-{T_{1}})[1-2{a_{r}}{(1-k)^{2}}]^{-1}}} \) \( REF \_Ref133090330 \r \h \) \( [1] \) [4](4)

Figure 3. Reversible Stirling cycle P-V diagram [5].

4. Submarine: Stirling cycle with van der Waals gas as working fluid

In order to improve the circulation efficiency of two isotherms and two isothermal lines, Scotsman Robert Stirling thought of a wonderful method of built-in recuperator, so that the absorption and exothermic heat of the two isothermal processes occur in the working fluid system, which is why the cycle is composed of two isotherms and two isothermal lines with a recuperator design, which is called Stirling cycle, the corresponding heat engine is called Stirling heat engine [1].

Let the temperature of the two isothermal processes be T1 and T2 respectively, we can see that \( {V_{1}}+{V_{2}}=V \) , V3=V4=rV. Let the cycle start from the initial state in Figure 1, then the cycle includes two endothermic processes 1-2 and 2-3, and two exothermic processes 3-4 and 4-1. Among them, k＝b/V is the ratio of the rejection volume of van der Waals gas to the initial volume of the cycle, and c is the miners' one power of γ minus one times one minus T one divided by T two. As can be seen from Equation 5 and Equation 6, the work and efficiency of the Stirling cycle are related to four parameters. That is, the adiabatic ratio γ and the temperature ratio T1 divided by T2 of the gas, the volume compression ratio r of the cycle, the ratio k of the repulsive volume of the gas to the initial volume of the cycle, the approximate expression of efficiency is obtained.

So η=25%-37%.

\( W=|{Q_{h}}|-|{Q_{l}}|=R({T_{2}}-{T_{1}})ln{\frac{({V_{4}}-b)}{({V_{1}}-b)}}=R({T_{2}}-{T_{1}})ln{\frac{(r-k)}{(1-k)}} \) (5)

\( η=1-\frac{|{Q_{l}}|}{|{Q_{h}}|}=\frac{R({T_{2}}-{T_{1}})ln{\frac{({V_{4}}-b)}{({V_{1}}-b)}}}{C_{V}^{0}({T_{2}}-{T_{1}})+R{T_{2}}ln{\frac{({V_{3}}-b)}{({V_{2}}-b)}}}=\frac{(1-\frac{{T_{1}}}{{T_{2}}})}{cln{{^-1}\frac{(r-k)}{(1-k)}+1}} \) \( REF \_Ref133090330 \r \h \) \( [1] \) (6)

5. Thermal power plant: Rankine cycle with van der Waals gas as working medium

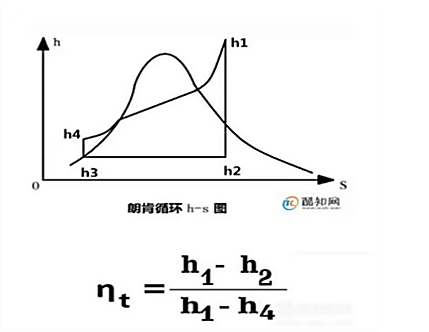
Figure 4. Rankine cycle h-s diagram [5].

\( η=\frac{(1-\frac{{T_{1}}}{{T_{2}}})}{cln{{^-1}r+1}}+\frac{c(r-1)(1-\frac{{T_{1}}}{{T_{2}}})}{r(c+ln{r})}k \) \( REF \_Ref133090330 \r \h \) \( [1] \) (7)

h=heat

S=entropy

12:Turbine expansion;

23:Heat release of the condenser;

34:Feed pump compression;

41:Boiler heat absorption;

Turbine work is h1 minus h2

Constant pressure heat release in the condenser, plot 12: h2－h3

Heat insulation and compression consumption of water pump, plot 34: h4 minus h3

Heat absorption at constant pressure in the boiler: h1 minus h4

The work done in process 3 to 4 is negligible.

The thermodynamic Rankine cycle turns heat energy into work. The Rankine cycle converts outside heat into work by heating its closed-loop working fluid, commonly water. The mid-19th-century Rankine cycle hypothesis still generates 90% of the world's energy, including practically all solar thermal, biomass, coal, and nuclear power facilities. Steam engines are based on the Rankine cycle[6].

Thermal efficiency: Evaporator outlet temperature.

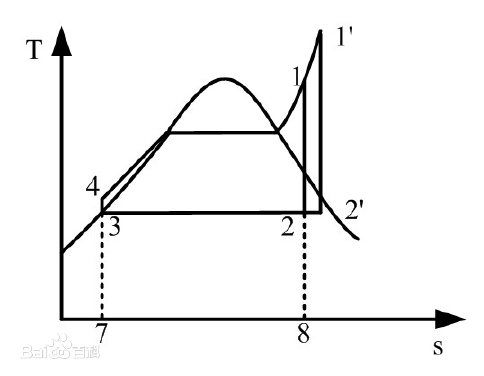
Figure 5. Effect of evaporator outlet temperature on thermal efficiency [5].

When the evaporation and condensation pressures are constant, raising the working fluid evaporator output temperature increases thermal efficiency [1]. When the evaporation temperature is raised from 1 to 1', the average endothermic temperature rises, increasing the circulating temperature differential and circulating heat efficiency. The end-of-expansion dryness of the circulating working fluid rises with evaporation temperature, which improves expansion equipment performance and service life.

Evaporation pressure and thermal efficiency:

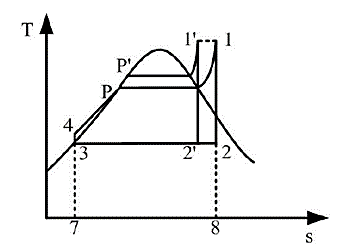
Figure 6. Effect of evaporator outlet temperature on thermal efficiency [5].

Figure 6 shows that evaporation pressure enhances system efficiency when the condensing pressure and evaporation temperature are constant. The average endothermic temperature rises when the evaporation pressure rises from P to P', increasing the Rankine cycle's average temperature difference. Equivalent Carnot efficiency states that system efficiency increases with average temperature difference. Evaporation pressure boosts cycle thermal efficiency. Excessive evaporation pressure might potentially harm the system.

Condensation pressure on thermal efficiency:

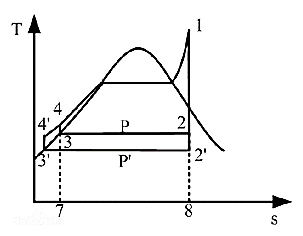
Figure 7. Effect of condensation pressure on thermal efficiency [5].

Figure 7 shows that decreasing condensing pressure at the same evaporation temperature and pressure enhances thermal efficiency. The average exothermic temperature drops as the condensing pressure is dropped from P to P', increasing the circulation temperature differential and thermal efficiency. Reducing condensing pressure does not improve thermal efficiency. This is because the saturation temperature of the working fluid corresponds to the saturation pressure one-to-one, and reducing the condensing pressure will lower the saturation temperature in the condenser, which must be higher than the ambient temperature to ensure system operation. Second, to prevent negative pressure and impurity penetration, the pipeline pressure is usually greater than ambient pressure [7].

6. The result of different machines use different cycles

6.1. Gasoline engine uses Otto cycle

Otto cycle cost is relatively low.

The operation is smooth, the engine structure is relatively simple

The gas distribution mechanism can achieve high-liter power without special tuning, and the engine can provide better power output at various speeds.

6.2. Diesel engine uses diesel cycle

Diesel cycle efficiency is relatively high and diesel engine load is relatively heavy. This internal combustion engine does not require an ignition device, so it is more simplified in structure than gasoline engines. At the same time, it begins to suck pure air into the cylinder, not a mixture of air and fuel, so that when the compression pressure is increased, no "deflagration" occurs. In this way, the compression pressure can also be increased, so that the compressed air temperature reaches or exceeds the ignition point of diesel fuel, igniting diesel fuel. Diesel believed that diesel is very powerful when burning, so the internal combustion engine using diesel is an engine with a large output power.

6.3. Submarine uses the Stirling cycle

Energy-compatible. A heat carrier system (such as a heat pipe) may utilise nearly any high-temperature heat source, including biomass energy (firewood, etc.). While the engine itself (except for the heater) does not need any changes and the hot gas engine does not need compressor pressurization, the use of general fans can meet the requirements and allow the fuel to have a high impurity content. Stirling engines are commonly used for solar energy and radioisotopes in submarine and deep space AIP systems.

Quiet. The hot gas engine's continuous fuel burning eliminates knocking and sporadic combustion, resulting in minimal noise. It can be concealed aboard submarines. Hot gas machines have a modest unit capacity of 20-50 kw, which can enhance or reduce system capacity depending on local conditions. Simple structure, 40% fewer parts than the internal combustion engine, huge price reduction space, and low maintenance cost.

Air pressure-insensitive. Stirling closed cycles isolate working fluids from the environment. It's suitable for high elevations.

7. Some better ways to improve it

7.1. With gasoline engine

Some optimization of intake and exhaust system: variable valve timing, variable valve lift, the final goal is to reduce the loss of pump air, and realize three cycle switching, which is Otto, Miller, and Atkinson.

7.2. With diesel engine [5]

For dozens of friction pairs on the machine, the clearance shall be kept as standard as possible, the lubrication shall be kept in good condition, and the noise and friction shall be reduced.

Oil supply time shall be correct.

Diesel oil grade, diesel oil quality standard.

Redesign the combustion chamber to better mix diesel and air; While adopting a four-valve structure, the injector is arranged in the middle of the cylinder, and the four-valve structure expands the total circulation area of the intake and exhaust valves and reduces the intake resistance compared with the two-valve structure. The four-valve structure can also make the injector arranged in the middle of the cylinder to improve the distribution of diesel and air in the combustion chamber so that the diesel and air are fully mixed.

7.3. With thermal power plant:

Improving steam parameters: improving steam parameters can increase the heat carried by unit volume steam and increase its working capacity. The steam exhaust capacity of the turbine is reduced correspondingly, and the heat released by the exhaust steam in the condenser and carried away by the cooling water is reduced.

Intermediate reheating: the steam with reduced pressure and temperature after being expanded and worked in the HP casing of the steam turbine is led back to the reheater in the boiler for reheating to the temperature of superheated steam. Then it is led back to the LP casing of the turbine to continue to work.

8. Conclusion

In conclusion, this study aimed to compare the engine efficiency of different types of engines and evaluate their thermal efficiency, brake power, and specific fuel consumption. The results showed that the diesel cycle had higher thermal efficiency and brake power compared to the Otto cycle. Meanwhile, the two-stroke engines had lower specific fuel consumption compared to the four-stroke engines. These findings suggest that both types of engines have their strengths and weaknesses, and the choice of the engine should depend on the specific application and requirements. Therefore, it is essential to consider the engine type, cycle, and fuel consumption when designing and selecting engines for different applications, including the automotive industry, submarines, and thermal power plants. Further research is needed to explore other factors that affect engine efficiency, such as fuel type, combustion chamber design, and operating conditions.

When conducting a study on engine efficiency, several limitations need to be considered. The following are some of the limitations of this study:

Small Sample Size: This study was conducted on a sample of only two engines, one internal combustion engine, and one external combustion engine. While these engines were chosen to represent different types of engines, a larger sample size would have provided a more comprehensive comparison of different types of engines and their efficiency.

Limited Scope: This study only evaluated the engines based on their thermal efficiency, brake power, and specific fuel consumption. Other factors such as emissions, noise levels, and durability were not taken into consideration. Therefore, the results of this study cannot be used to make a comprehensive comparison of different types of engines.

Engine Variations: Even within the same engine type, there can be variations in design and performance. For example, different types of diesel engines can have different compression ratios, which can affect their efficiency. Therefore, the results of this study cannot be generalized to all engines of the same type.

External Factors: The efficiency of an engine can be affected by external factors such as weather conditions, altitude, and load. This study did not control these factors, which may have affected the outcomes.