1. Introduction

Conventional computing based on vacuum tubes and microprocessors have already been used since 19th century. During these years, Moore’s Law, which have been working for nearly 60 years, predicted that the transistor would double every two years [1]. Over the years, many people have argued that it will die because the physical element cannot go smaller and smaller until nothing [2]. However, the arrival of Quantum computation may give the development of computers another possibility. The Bell’s experiment has refuted the localized hidden variable model [3]. In addition, quantum supremacy experiment debunks “the Extended Church-Turing thesis” [4], because a conventional computer can’t stimulate a quantum state [5]. These all lead to one conclusion, the speed and capacity of a quantum computer will have a better performance.

The criteria of deciding whether a model is efficiency for realizing quantum computation is DiVincenzo’s Criteria [6]. Recently, scientists have tried for various kinds of materials to realize quantum computation. Trapped-ion-systems have already demonstrated almost of the basic requirements for universal QC [7]. Superconducting quantum circuits also is experiencing a rapid development [8]. However, although the possibility of using Majorana fermions to realize quantum computation was come up in, the physical realization is still at its start [9]. That’s because it has not been observed until 2012 [10]. Further observations and relative physical research are slowly carried forward after that. Majorana fermions are considered to be idea materials of quantum computation because when a pair of Majorana fermions are combined, they can act as perfect qubits. Because of its special topological properties, more research is being done on it recently.

To analyse the recent progresses in realizing quantum computation by Majorana fermions, and to provide some complete information for the latter research, this study concludes the main researches about the Majorana fermions and introduced their significant progresses. For the first part, this essay introduces the definition and the discovering of Majorana fermions. Then, the article talks about some special properties of fermions. It is subject to non-Abelian statistics, which makes the scientists can use these properties to achieve quantum computing. Then this paper explains some algorithms and codes based on Majorana that can be implemented at present. Finally, the passage predicts the future development and the problems it will encounter.

2. Majorana fermions

Majorana fermions was first come up at 1937 by Italian Physician Majorana [11]. He predicted there exist a kind of particle that is its own antiparticle, or in the language of second quantization:

\( γ={γ^{†}}  \ \ \ \) (1)

One can easily construct a pair of Majorana fermions. Consider a condition that with two infinite potential wells

\( H=-\frac{1}{2m}\frac{{∂^{2}}}{∂{x^{2}}}-V(δ(x-\frac{L}{2})+δ(x+\frac{L}{2}))    \ \ \ \) (2)

When define the basis states

\( {Ψ_{l,r}}=exp{(-|x∓\frac{L}{2}|/ξ)}  \ \ \   \) (3)

The Hamiltonian can be rewritten as

\( H=-ϵ(c_{l}^{†}{c_{l}}+c_{r}^{†}{c_{r}})-J(c_{l}^{†}{c_{r}}+h.c)    \ \ \ \) (4)

On this basis, one can find the Majorana operators

\( {Γ_{+}}=c+{c^{†}}, {γ_{-}}=-i(c-{c^{†}})    \ \ \   \) (5)

γ+ and γ_ satisfied:

\( \lbrace {γ_{+}},{γ_{-}}\rbrace =0  \ \ \   \) (6)

\( γ_{±}^{2}=1        \ \ \ \) (7)

\( {γ_{±}}=γ_{±}^{†}       \) (8)

So obviously, they are a pair of Majorana operators. The Hamiltonian can be altered to

\( H=-ϵi({γ_{l+}}{γ_{l-}}+{γ_{r+}}{γ_{r-}})-i\frac{J}{2}({γ_{l-}}{γ_{r+}}-{γ_{l+}}{γ_{r-}})   \ \ \ \) (9)

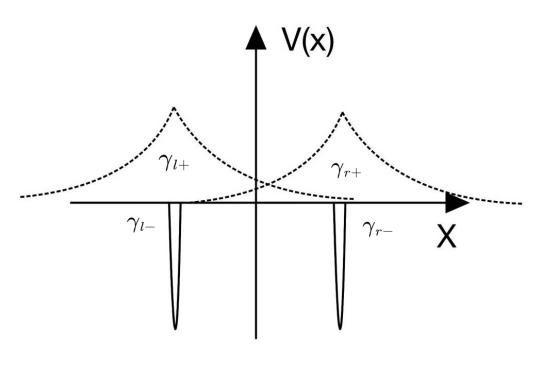
Figure 1. The two well state system.

Figure 1 shows the Potential energy diagram of the two well state system. According to Kitaev, any of the for states can be operated independently. With Kitaev’s special trick [12], one can separate these two states, so that one can operate on each of them. When one makes the chain linked, one gets

\( H=\frac{1}{2}\sum _{i}(-iϵ{γ_{i+}}{γ_{i-}}-iJ{γ_{i+}}{γ_{(i+1)-}})     \ \ \ \) (10)

Let’s set Ɛ=0, so the creation and the annihilation operators can be writing as:

\( {d_{i}}={γ_{i+}}+i{γ_{(i+1)-}}, d_{i}^{†}={γ_{i+}}-i{γ_{(i+1)-}}    \) (11)

These gives us a new formula

\( [H,{γ_{0+}}]=[H,{γ_{L+}}]=0       \ \ \   \) (12)

While the first part is the left side, the second is the left. So finally, the two state can be separated. In 2010, it was discovered that nanowires and s-wave superconducting and magnetic fields with Rashba spin orbit coupling could implement Kitaev's toy model, thus achieving Majorana bound states [13]. Although the theoretical analyses of Majorana fermions are very deep, scientists first measure them in 2012 [10]. Since then, many scientists have provided strong evidence that support the existence of Majorana fermions. In 2017, an essay published on Science claimed that they discovered Chiral Majorana fermion in a superconductor structure, quantum anomalous Hall insulator. However, this paper caused great controversy and was retracted because of “insufficient scientific rigor” [14]. This is a huge blow to researches in this field. But physicists keep going. In 2020, Wang observed some signatures of Majorana quasiparticles in FeSexTe1−x, a kind of superconductor [15]. Yet this evidence have so far failed to lead to a solid foundation of its existence.

3. Principle of quantum computing for Majorana fermions

The particularity of fermions shows some remarkable special properties, such as topology. These make it possible for fermions to implement quantum computing. Firstly, Majorana fermions always appear in pairs, and in Kitaev’s toy model [12], each fermion can be operated independently. To realize the quantum bit, one needs a well state with a good superposition. But since there’s no system that is at a superposition of two parity states, one needs to use another two Majorana to make a qubit. Thus, one can use two pair of Majorana A and B to get an even state \( |{0_{A}}{0_{B}} \gt ,|{1_{A}}{1_{B}} \gt \) . The odd parity state is similar.

Now one will do some trick to realize some single qubit gate. Define:

\( |{0_{A}}{0_{B}}≥ζ(|{0_{+}}{0_{0}} \gt +α|{1_{+}}{1_{-}} \gt ) \ \ \ \) (13)

\( |{1_{A}}{1_{B}}≥η(|{0_{+}}{0_{0}} \gt +β|{1_{+}}{1_{-}} \gt ) \ \ \ \) (14)

\( {c_{+}}=\frac{1}{2}({γ_{A+}}+i{γ_{B+}}), {c_{-}}=\frac{1}{2}({γ_{B-}}+i{γ_{A-}})   \ \ \   \) (15)

Thus, the creation operators can be written as

\( {c_{A}}=\frac{1}{2}({c_{+}}+c_{+}^{†}+i\frac{1}{i}({c_{-}}-c_{-}^{†})), {C_{B}}=\frac{1}{2}(\frac{1}{i}({c_{±}}c_{+}^{†})+({c_{∓}}c_{-}^{†})) \ \ \    \) (16)

Since

\( {c_{A}}|{0_{A}}{0_{B}}≥{c_{B}}|{0_{A}}{0_{B}}≥0 \ \ \ \) (17)

\( c_{A}^{†}|{1_{A}}{1_{B}}≥c_{B}^{†}|{1_{A}}{1_{B}}≥0 \ \ \ \) (18)

After substituting Eq. (17) and Eq. (18) into Eq. (16), there is

\( ({c_{+}}+c_{+}^{†}+({c_{-}}-c_{-}^{†}))(|{0_{+}}{0_{0}} \gt +α|{1_{+}}{1_{-}} \gt )=|{1_{+}}{0_{-}} \gt -|{0_{+}}{1_{-}} \gt +α(|{1_{+}}{0_{-}} \gt -|{0_{+}}{1_{-}} \gt )  \) (19)

If one uses the basis

\( |{0_{A}}{0_{B}}≥\frac{1}{\sqrt[]{2}}(|{0_{+}}{0_{0}} \gt -|{1_{+}}{1_{-}} \gt ) \ \ \ \) (20)

\( |{1_{A}}{1_{B}}≥\frac{1}{\sqrt[]{2}}(|{0_{+}}{0_{0}} \gt +|{1_{+}}{1_{-}} \gt ) \ \ \   \) (21)

One can start to get some qubit gate.

\( {T_{{A_{+}},{B_{+}}}}|{0_{A}}{0_{B}}≥\frac{1}{\sqrt[]{2}}({T_{+}}|{0_{+}}{0_{-}} \gt -{T_{+}}|{1_{+}}{1_{-}} \gt )=\frac{1}{\sqrt[]{2}}(|{0_{+}}{0_{-}} \gt +|{1_{+}}{1_{-}} \gt )=|{1_{A}}{1_{B}} \gt   \ \ \   \) (22)

So, one gets a NOT gate. \(   \)

\( \begin{array}{c}            {E_{+}}|{0_{A}}{0_{B}}≥\frac{1}{\sqrt[]{2}}({E_{+}}|{0_{+}}{0_{-}} \gt -{E_{+}}|{1_{+}}{1_{-}} \gt )=\frac{1}{\sqrt[]{2}}(|{0_{+}}{0_{-}} \gt -i|{1_{+}}{1_{-}} \gt ) = \\ \frac{1}{2}((1+i)|{0_{+}}{0_{-}} \gt +(1-i)|{1_{+}}{1_{-}} \gt )  \ \ \   \end{array} \) (23)

This is a realization of Hadamard gate [11].

In conclusion, people can use the Majorana fermions to construct some Quantum gates, which is significant to the realization of quantum computation. In addition, Majorana zero modes (Majorana) is a kind of non-Abelian, which means it obey non-Abelian braiding statistics. Consider a pair of Majorana fermions, and when one exchanges two fermions A and B, γB goes through the string of γA. As a result, one derives \( {γ_{A}}→-{γ_{B}} \) and \( {γ_{B}}→{γ_{A}} \) , as a result:

\( {γ_{A}}+i{γ_{B}}→-{γ_{B}}+i{γ_{A}}=i({γ_{A}}+i{γ_{B}})   \ \ \ \) (24)

Obviously, the state is multiple by an i. If one does it again, one will get a -1. This is the property of non-abelian statistics. This makes it the most promising way to realize a fault-tolerant quantum computer. [16]. Since Topological quantum computation is one of the most exciting approaches to constructing a fault-tolerant quantum computer; non-abelian particles give this approach possibility to realize. Topological quantum computation is a way that can realize the quantum computation with non-Abelian braiding statistics. Scientists braid quasiparticles to operate in this subspace. While the local perturbation as the hyperfine electron-nuclear interaction as well as the electron-phonon interaction happened, decoherence in the nontopological solid state will happen. The degenerate ground states have a subspace, whereas this kind of evolution is strictly constrained. As for non-abelian particles, because any local perturbation doesn’t have any nontrivial matrix elements within the ground state subspace, it is naturally immune to errors, i.e., rather immune from decoherence [16]. Majorana fermions are also proved that it can be measured by using only the statistics of measurements outcomes. Abu Ashik Md. Irfan etc. have indicates the confidence level of the detection of Majorana fermions [17].

4. Coding and algorithm

In the previous section, one has shown that Majorana fermions can do much on quantum computing, and this article will now introduce some of the code and algorithms that fermions have implemented. They show amazing advantages and are likely to be realized. Indeed, there are many proposals base on Majorana fermions. In 2015, Liang Fu etc. proposed a physical implementation based on bosonic surface codes [18].

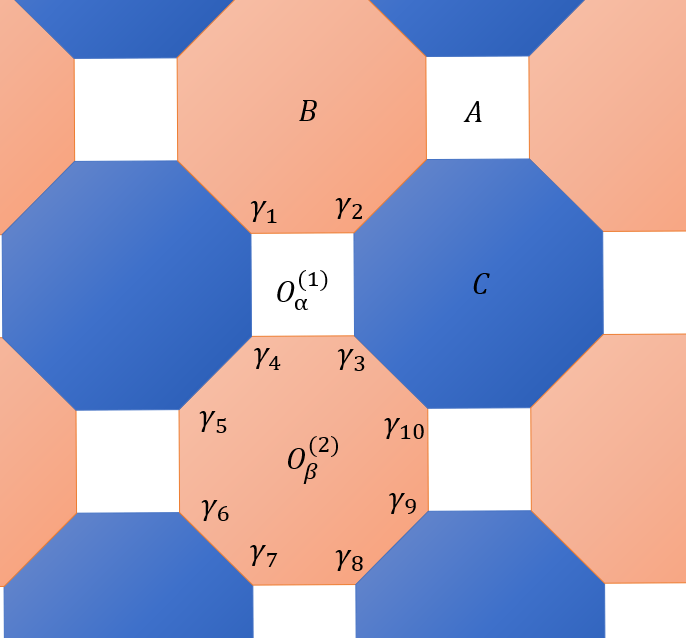
Figure 2. An octagon lattice with a Majorana fermions on its vertexes. A, B, C represent three different kinds of fundamental excitations. They can be created by acting string-like Wilson line operators on the ground-state.

They use a hybrid strategy which takes advantage from both the static parent Hamiltonian and projective measurements to provide the error correction capability. As shown in the Figure 2, the Hamiltonian, which is the sum of the fermion parity of plaquettes, can be wrote as

\( {H_{0}}=-{u_{1}}\sum _{α}O_{α}^{(1)}-{u_{2}}\sum _{β}O_{β}^{(1)}   \ \ \ \) (25)

In the array of Josephson coupled topological superconductors, this Hamiltonian is proved to be realizable. With the superconducting qubit technology, the measurement can be realized as well, so that a Majorana fermion surface code is implemented by combination of designing a static Hamiltonian and performing constant measurements.

Advanced algorithms are coming up recently, besides bosonic surface code, there are also bosonic colour codes, fermionic surface code etc. In addition, Daniel Litinski et al. have established a new kind of framework, which can maintain the advantage in zero-overhead single qubit Clifford gates of Majorana fermions. This means that all kinds of Clifford gates can be implemented with zero-time overhead. Therefore, by appropriately designing Operations on logical qubits, people can track all Clifford gates, so that zero-time overhead is used by these gates. They designed a quantum computer similar to Figure 3 [18]. They use tetrons and hexons to construct an array to compute. A part of this array is used to extract the “magic state” and the other parts are used to encode the data qubits. While they are replaced by the logical ones and are arranged in appropriate code distance, the topological quantum computation can be realized [19].

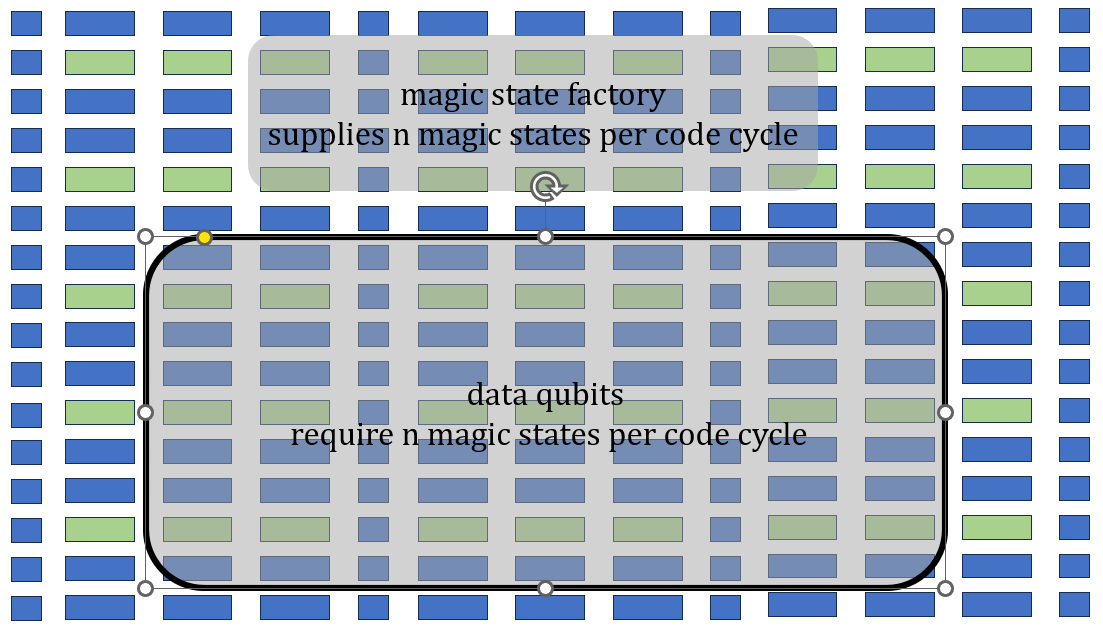
Figure 3. Tetrons and hexons are both used to construct an array to compute [18].

To sum up, there have been a lot of physically meaningful implementation of Majorana-based coding methods. These applications provide scientists with more confidence and motivation to explore the existence of fermions, enhancing confidence in the development of the field of topological quantum computing.

5. Limitations and prospects

This article summarizes the recent development of Majorana fermions mainly from a theoretical point of view. The superiority of Majorana fermions in topological quantum computation is included. Some Majorana-based algorithms are also illustrated. In theory, these algorithms have been proved to have very good fault tolerance. On the other hand, the research in this paper mainly focuses on the theoretical aspects, and the practical applications are not mentioned. There are still some challenges to observe Majorana experimentally. For example, current experimental methods have not yet been able to achieve direct imaging of a single Majorana zero mode, which limits the study of its spatial structure [20]. The concept of Majorana fermions was proposed as early as 1937. In the last two decades, with the development of science and technology, there has been a lot of research on it. From a theoretical point of view, a great deal of Majorana fermions research has so far focused on the field of superconductivity, leading to the neglect of its great potential in topological quantum computing. With the discovery of the great potential of topological quantum computing in the field of fault-tolerant quantum computing, people's interest in Majorana-based quantum computation increased. There are many researches on Majorana-based algorithms and codes, mainly focusing on bosonic surface or colour codes, fermionic surface codes, and small Majorana fermion codes. In terms of the field of finding, or proving, Majorana fermions in experiments has actually stalled over the years. This has also caused great obstacles to scientific theoretical research.

6. Conclusion

To sum up, this study presents an application of Majorana fermions to quantum computing. The paper contains the current state of the art in quantum computing and the role of Majorana fermions in it. This study discussess the principle of quantum computing for Majorana fermions. Moreover, this paper introduces some codes and algorithms that can be implemented by Majorana fermions. In the last two decades, more and more research has been done on Majorana fermions. Despite some setbacks, most people still have faith in the practical application in this area. The further development of Majorana fermions in the future still depends on the simultaneous development of theory and experiment. By analysis of the development of Majorana fermions research in recent years, it is hoped that this article will introduce some basic concepts and developments to those who want to engage in fermion-related research.