1. Introduction

Some people would probably stress that random walks derived from investigations on gambling back in ancient times. However, in fact, people came to see and learn about random walks during 1900s [1]. The very first person who demonstrated the problem of random walks in a letter to Nature was Karl Pearson in the early 20th century. His problem was mainly based on the fields of biology and medicine [2]. He proposed the problem as follows: “A person begins at the origin and moves l yards straightly; he changes his direction when he finishes the first part of his journey as l yards. He keeps on doing the same procedure again and again. What is the probability that after many steps, the distance from the origin to him is bounded by r and r + dr [3].” A year later, Kluyver came up with a perfect answer to the question. After that, Rayleigh successfully dealt with random walks in a three-dimensional space. Chandrasehkar further elaborated Rayleigh’s result for identical movements. Watson composed a document to record the deduction of the more ordinary condition. In 1920s, George submitted his paper in which he tried to compute the probability of a particle beginning its journey at the starting point and getting back to the same position ultimately. The application of random walks was initiated by Taylor. He applied a continuous-time random walk to simulate the impetus of turbulent diffusion. During 1930s and 1940s, Kuhn and Grun imaged the structure of polymer chains, which stimulated other scholars to conduct research on random walks [1].

Nowadays, predecessors have already widely applied random walks in a variety of fields. For instance, continuous-time random walks (CTRW) can be used to calculate the ruin probability in insurance [4]. In order to achieve this goal, one might be able to make a use of the equation for the risk process and define when the company would ruin and therefore understand the probability of being ruined. By computing the average value of Monte Carlo methods, one can approximate the probability that the insurance company would go bankruptcy during a certain amount of time. On the other hand, one has to spend a large amount of time with theories to figure out the same probability in an open interval of time. Nevertheless, the mathematical approach is much more complicated. Therefore, several scholars suggest that it is better to estimate the claim of compensation according to Brownian motion since the claim can be described as a continuous-time random walk.

Moreover, floating random walks facilitate to find solutions of heat equations [5]. The floating random walks claim that how long will you take a step or grid points are not chosen at the beginning. In a non-recurrent case, the length of time taking each movement is different. Consequently, the Monte Carlo method has nothing to do with the outline of the terminal requirements. Additionally, in a traditional approach for collecting samples, the mean value of changes greatly exceeds that in a random walk. As a result, the complexity of calculations falls sharply. Furthermore, random walks in one-dimensional space when the disappearance of a particle is possible at every single movement can be used to interpret the behavior of protein on DNA [6]. It turns out that in the disappearing situation, the distance from the origin to the end has nothing to do with the mean value of the molecule’s movements arriving the terminal position eventually in terms of a quadratic function. As the distances become larger and larger, the relationship approaches a linear function. The reason for such phenomenon is that the missing particle often choose the optimal route initiating from the origin to the destination. Thus, one is able to study the migrations of protein inside complex DNA matters.

The purpose of this paper is to review on the principle and three thought-provoking applications of random walks in terms of multilayer networks, predation and stock market. The organization of the text is described as follows. For the part involving principles, the paper will focus on some basic descriptions of random walk such as concepts and definitions. The next session is related to application. The first application has its connection with computer science. The second biological scenario considering a foraging predator. The last application is aimed at the role of random walks in finance and market efficiency. Afterwards, the paper will discuss limitations and future outlooks of random walks. The conclusion will be drawn at the end of this paper.

2. Basic Descriptions of Random Walks

There are two important concepts to define a random walk. One is the state space. The other is the transition probability. The state space is simply all of the states that are accessible in a given space. The transition probability from one state to another is the probability of switching into another state from the previous state. First of all, one considers a symmetric random walk-in dimension one. A particle starts at the origin and can move either left or right, each with probability of one-half. In this case, the state space is the whole number axis, and the transition probabilities are the same, which are equivalent to one-half. It had already been proved that in a one-dimensional case, the probability of returning to the origin eventually is just 1. Therefore, the state of 0 is recurrent [7]. Similarly, in a two-dimensional case, the state space is a coordinate plane. Since the particle has four directions to go, namely left, right, up or down, the transition probabilities are equal to one fourth. By formulating the sum of returning to the origin at last for the first time and using Stirling approximation, one is able to show that the starting point is again recurrent in dimension two. On the contrary, a random walk-in dimension three differs from that in lower dimension. For beginners, it is better to think about the complexity of reaching the original point since the particle has to ensure that when it is at the origin of the x-axis, it should be at the starting point of the y-axis; when it is at the beginning point of the y-axis, it should be at the origin of the z-axis; and when it is at the origin of the x-axis, it should also be at the starting point of the z-axis. As a result, the origin state is transient. On the other hand, the same result could be shown as the case in dimension one and two.

Another definition of random walks is the procedure made by a series of sum of random variables with the property of independence and with the same probability. Contemporarily, people are making use of random walks to handle sophisticated problems. To be more specific, researchers who apply random walks in a large number of realms often need to derive a much more accurate estimation of the variation of such random walks due to the fact that central limit theorem only offers a rough result. In fact, computing how large the error bound is regarding to random walks is significant to modern scientific research [8]. There is also a book which specializes in discussing random walks in dimension two because the property of such case is well studied by former scholars. The subtle relationship between harmonic analysis and potential theory indicates the importance of random walks in the world of science [9].

3. Application of Random Walks to Multilayer Networks

The size of social networks has grown significantly, and it is now more challenging to gather information about the whole network as a result of the rapid expansion of information networks. Further, as the existing mining technique for complex network communities relies on knowledge of node linkages or features, it is unable to accurately identify those with thick member relationships and strikingly comparable characteristics. Thus, the majority of present algorithms are unsuitable for massive social media platforms. Researchers have therefore developed the local random walk-based community detection algorithm (MRLCD) for multilayer social networks, which identifies the core node depending on the recurrence of multilayer nodes [10]. There are various techniques to find rich “communities” of vertices in multilayer networks, which is one of the currently popular fields in network research. A common approach to describe a community consists of a collection of nodes that over an extended period of time, capture a diffusion-like kinetic activity (often a random walk). According to this perspective, communities can be groups of nodes that obstruct a dynamic operation’s ability to expand over a network. The performance of community-detection techniques that depend on such random walks is directly affected by the analysis of the local patterns of various random walks on multilayer networks [11]. While applying random walks, it is common to want to ensure that each node has an entire relevance score. It is reasonable for us to anticipate that the measurements will take the significance derived from the various level into consideration because the device under consideration comprises a number of actor-actor relationships.

One of the most basic fluctuations that may take place on a network is a random walk, and random walks give a hand to researchers to mimic different varieties of diffusion processes. Given their significance and readability, random walks on networks have garnered a lot of curiosity. They may be explored statistically and have produced major discoveries on a wide range of situations. In particular, random walks are currently implemented to evaluate websites and athletic groups, improve outcomes from searches, examine the effectiveness of online directions, describe cyclic patterns in systems, and reveal mesco-scale aspects like civic groups in coarse -grain networks as well. Random walks may also be used to determine the centrality of players in intricate systems when only regional data are accessible while the network’s overall layout is unclear. Regarding these circumstances, random walk-based centrality ideas should be used in place of centrality classifiers built around shortest routes, such as betweenness and proximity centrality. One expands these methods to multilayer networks in the sections that accompany.

Initially, let us establish a discrete-time random walk as an ordered set of arbitrary nodes that begins at node a in any layer and stops at node b in any layer, with each edge’s ends being the previous and subsequent vertices in the pattern, on a multilayer network with L layers and N nodes per layer. This concept is justified by the fact that everything that travels between the many node copies in the various levels relates to the identical element, regardless of the originating layer or finishing layer. Fig. 1 illustrates a case of a random walk between two nodes in a multilayer network where it is clear that significant influences have been introduced and have an impact on the flow of the connected device due to the existence of inter-layer linkages.

Figure 1. Schematic diagram of a random walk between two nodes a and b in a multilayer network.

Each tensor representing the average initial travel time to node b, given that the random walk begins at node a in layer σ, is

\( {({H_{[b]}})^{aσ}}=\sum _{t=0}^{∞}t{({q_{[b]}})^{aσ}}(h=t)=[{(δ-{T_{[b]}})^{-1}}]_{jβ}^{aσ}{u^{jβ}}\ \ \ (1) \)

Additionally, it has already been shown that the mathematical equation supplied are prepared to be used in the study of actual complicated networks since there is complete consistency in the assumptions made by the method used and the simulation findings [12].

4. Application of Random Walks to Predation

Animal behaviors of search are frequently referred to as random walk to depict circumstances in which the precise position of the objective cannot be predicted in advance and when more complicated search tactics are not supported by one’s cognitive constraints and environmental variables. The idea of random walks has been substantially studied and utilized in a variety of situations, from animal behavior to people cognition, from the pioneering investigations of the botanist Robert Brown regarding the mobility of pollen particles, known as Brownian motion [13]. To stay alive, all animals need to feed. It follows that for some hunter species, there must be enough prey to pursue after and kill. Predators are continuous searching for meals. Thus, victims need to stay aware. While groupings of animals frequently separate and wander to fool an approaching attacker, if ways to fee are not properly organized, single prey can additionally obstruct one another [14].

Determining how complicated animals disperse themselves over time and distance in quest of objects like nourishment, warmth, or partners requires the implementation of crucial tools like random walk simulations. Agent-driven systems make it simple to study these routes and may be applied to determine the optimum search method given a particular effectiveness indicator. The whole spectrum of feasible random walks, success measures, and walker limitations are often not taken into account in present study, and the execution features differ greatly. Thus, it can be tough to assess the outcomes of different investigations. One creates the four motion models (BW, CorRW, ComRW, and CCRW) in the parts that com after, parts 4.1-4.5. This study first outlines the Brownian walk (BW) simulation technique before creating the other three motion models. Lastly, this paper demonstrates that one central model with the rest models can be used to understand the four motion models.

A Brownian walk (BW) is a traditional random walk. The walker selects a stride size and angle of motion from an exponential and uniform distributions, respectively, at each stage of its operation. The outcome is a random walk with no indication for orientation and an average step size equal to the reciprocal of each step size. In biological modeling, correlated random walks (CorRW) feature an extensive background (seen from Fig. 2). A random walker chasing a CorRW selects each stride size from an exponential distribution, much like the BW. Nevertheless, since the angle of each subsequent step is associated, orientation endurance is included to the BW. In models with orientation endurance, several motion orientation distributions have been employed. From wrapped Cauchy distributions through von Mises distributions, famous distributions include wrapped Normal distributions. Two BWs with various average step sizes are combined to form the composite random walk (ComRW). Small movements belong to the intense search mode (ISM), whereas big steps are associated with the extensive search mode (ESM). Each BW belongs to a distinct search mode. The walker alternates between each of these two types of searches. The BW, CorRw, and ComRW are all included in the correlated composite random walk (CCRW). As shown by stepsize patterns with two distinct averages (a ComRW) and orientation consistency (a CorRW) during ESM motion, the CCRW random wanderer moves simultaneously in the ISM and ESM directions. Because orientation endurance only exists in the ESM, it should be noted that the walker has to take at least two steps in succession in the ESM for orientation endurance to happen. Both the angle that the model creature was traveling during the prior (intense) time step and the preceding session of ESM steps are not remembered by the model creature. These hypotheses reduce the model and are typical of physical modeling with RWs.

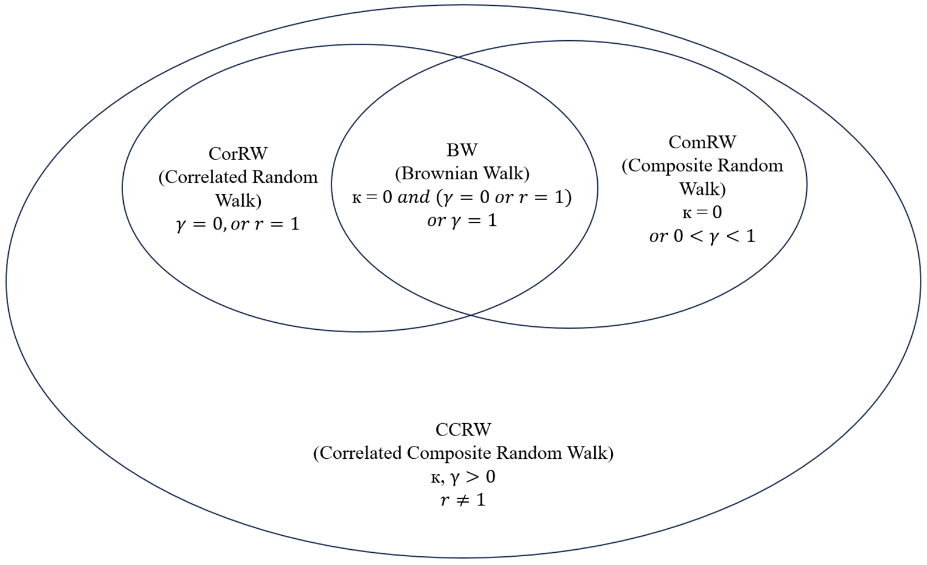
Figure 2. Schematic diagram explaining the three-dimensional random walk space characterized by the variables \( (r, γ,к) \) interacts with all of the motion models.

Finally, the widely held belief that CCRW motion habits ought to always function better than BWs has been validated, however, there are interesting instances when different walks do better. There are many different potential walks that fall belong to the CCRW type, and these walks are ranked based on energetic expense metrics. As a result of increased competition from evolution and a larger likelihood of adopting a virtually ideal random walk, CCRW predators who have little hunting achievement in a single mode have a greater tendency to do so [15].

5. Application of Random Walks to Stock Market

Researchers as well as investors have long been interested in the study on stock market efficiency and the random walk model (RWM) of returns on stocks. Additionally, developing stock markets frequently experience extreme swings. Table. 1 lists some of the results. As a result, there is now considerable study being done in this field in order to comprehend these marketplaces' features and look for clues inefficiencies. If these inefficiencies exist, buyers may be likely to take advantage of them in order to benefit. RWM's existence or exclusion has a significant impact on how knowledge is incorporated into pricing, which has crucial ramifications for the shareholders [16].

One excellent measure of every nation's financial stability is its stock market. As a result, financial experts are constantly quite interested in gauging the capital market in many ways [17]. The topic of the question of if stock markets are efficient is one of the most contentious between economists and these who decide about economic regulation. This topic has been extensively in the empirical research by putting the efficient market hypothesis (EMH) of Fama to the trial. The stock markets tend to be (weak type) effective, according to Fama, who claims that if the fluctuations of the price of shares are characterized by a random walk with movement. If the shares obey a random walk (unit) root procedure, any changes to the worth of the stocks are lasting, and the upcoming value of the stock is impossible to forecast from previous data. Additionally, it predicts that fluctuations in share prices is going to continue to grow as time passes. However, if stock prices track an average reversion (stationary) procedure, any fluctuations to cost levels are only going to be transient and will sooner or later likely to go back to the pattern’s trajectory. Shareholders may predict the potential worth of a company’s shares in this way, and doing so can lead to greater profits than the typical trade.

There is still disagreement among experts on the efficiency of stock markets, as seen by the rising body of actual studies on the random walk experiment in financial markets. It is possible to claim that the variations in the experimental outcomes of unit root analyses may be due to a number of factors. Primarily, a variety of fiscal incidents, e.g., economic recessions, deregulation initiatives, or adjustments to monetary policy, can have an impact on the stock market. Conventional unit root tests that ignore possible structural fractures may result in measurement biases and misunderstanding prejudice which might lead to false analytical judgments (Table 1).

Table 1. Selected unit root tests of Efficient Market Hypothesis.

Moreover, assuming that the economic cycle only contains a few physical breakdowns seems limited. Third, one can happen in inaccurate estimates is that typical unit root examination overlooks the possibility of cross-sectional dependencies among the participants. Consequently, it is still vital to investigate this problem using other statistical approaches and get additional knowledge for precise trading techniques for the purpose to comprehend the movements of share prices and reduce investor uncertainty.

Finally, the findings of the panel unit root tests contradict the null hypothesis, indicating that neither the value of shares nor stock markets are weakly efficient and that instead, prices cannot be explained by a procedure known as random walks. Nevertheless, current panel unit root evaluation methods that take changes in structure and cross-sectional dependence among datasets into account offer proof of the share markets' weak-form performance. This conclusion suggests that the present market values of shares incorporate and portray all previous data since it adopts the random walk nature of the price of stocks [18].

6. Limitations and Future Outlooks

Despite of the mentioned applications of random walks above, there are also several criticisms of random walks. For instance, the fact that there are many participants in the stock exchange and that every individual invests for various periods of time serves as one of the key objections of the Random Walk Theory. Other scholars contend that the Random Walk Theory's basic premise is incorrect and that, throughout a prolonged period, share prices do exhibit characteristics or patterns. They assert that it may be hard to determine the upward or downward trajectory observed in the value of a security since the price is influenced by an incredibly vast collection of elements. Now, one considers a case of a non-random walk. The claim of economic analysis proponents, who hold that price shifts in the future may be forecast by looking at established patterns, trends, and previous market activity, is in opposition to the Random Walk Theory. This viewpoint has the suggestion that merchants with greater knowledge of the markets and investing abilities can do noticeably better than the overall market mean. Each person is free to have any beliefs they select since either side may offer arguments to back up their assertions. Conversely, one single truth, possibly the most important one, contradicts the random walk hypothesis. It is actual that certain investors do continuously better than the financial mean over a lengthy amount of time. The Random Walk Theory states that an investor ought to just be likely to surpass the market mean through accident or good fortune. On the other hand, the chances that identical merchants would continue to be blessed every year for many years are in fact such investors, persons like Paul Tudor Jones, who have been able to consistently produce investing profits that are considerably higher than the norm in the marketplace over an extended period of time.

Nowadays, random walk has been widely used in an incredibly number of areas such as computer engineering, biology and economics discussed in the application sections. Random walk simulations may additionally be employed as a standard by which to contrast more intricate models of time series, especially regression models. The regression technique has a propensity to see R-squared as a gauge of the model's independent variables' capacity for prediction, although this isn't necessarily the situation. In order to forecast the dependent variable, R-squared calculates the difference between the error variance of the model using regression and the average of the model. This measurement, however, has little significance if the mean model is not a suitable reference source. It would appear more appropriate to ask the amount smaller the error variance of the model used for regression is than the error variance of the random walk model since, if the time sequence is nonstationary, a random walk model will frequently have a lot less error variance than the mean model. Despite the fact that a regression model has a high R-squared, it could perform poorer at estimating a time sequence than a random walk approach.

As a result, the random walk model is a crucial tool for our daily use, which is able to give us a hand to analyze and overcome a great series of complicated problems. With the development of technology and knowledge, people are likely to apply random walks in more and more creative and unbelievable ways.

7. Coclusion

To sum up, this study mainly focuses on the principle and some applications of random walk simulation. This paper has already discussed the history and meaning of studying random walks. Then, this study showed the research progress of random walks in terms of uses and results. After that, this paper offered a basic description of random walks by introducing their definition, mathematical statements, and common applications. Additionally, one reviewed three typical and intriguing applications of random walks to multilayer networks, predation, and stock market related to computer science, biology, and economics, respectively. In the first application, it is implied that the mathematical expression based on random walk models can help us handle complex networks. In the second application, various random walk models are used to keep track of a predator’s route. In the last application, however, random walks do not explain the fluctuation of stock prices. Finally, this study proposed limitations and future outlooks of random walks. In fact, it is not appropriate for us to model the prolonged success of an investor in the stock market by using random walk models. On the other hand, as time goes on, due to its essentiality, a random walk simulation might engage in other realms for overcoming obstacles in our life and work. This paper presents the development of random walks and facilitates readers to understand the importance of random walks in the contemporary society.