1. Introduction

The Hall effect was initially observed by Edwin Hall, an American scientist, in the year 1879 [1]. The researcher made an observation that the flow of electric current through a conductor results in the generation of a potential difference that is perpendicular to the direction of the current. This phenomena is commonly referred to as the Hall effect [2]. During the 1980s, Klaus von Klitzing, a physicist from Germany, conducted research on two-dimensional electronic vapors that were of exceptional purity. As a result of his investigations, he made a significant discovery regarding the quantization of conductivity when subjected to intense magnetic fields [3]. His experimental results show that the Hall conductance changes in quantized units (about \( 2.5×{10^{4}}{Ω^{-1}} \) ) [4], and when the quantization of the Hall conductance is due to the electrons being subjected to a strong magnetic field in a two-dimensional lattice, its energy bands are divided into multiple subdivision bands [5]. The Hall conductance of each subdivision band is equal to the Fermi constant multiplied by an integer, that is \( G=i×\frac{{e^{2}}}{h} \) , where G is the Hall conductance, i is an integer, e is the element charge, and h is Planck’s constant [6].

The fractional quantum Hall effect was discovered in 1982 by Francois Engelt, a Nobel laureate, in collaboration with Robert Laughlin and Horst Störmer. The researchers made an observation that in conditions of both extremely low temperatures and strong magnetic fields, a quantum state arises as a result of the quantization of Hall conductance. In this state, electrons exhibit a highly degenerate energy level structure due to the combined effects of quantum vortices and repulsive interactions [7]. The quantization of the quantum Hall conductance of fractions is indicated by the proportionate relationship observed between the number of degenerate levels and the corresponding fraction [8]. In 2005, prominent scientists in the field of physics, including Nobel Prize laureates Douglas Laughlin and Konstantin Novoselov, introduced the notion of topological insulators and made predictions regarding the presence of the quantum anomalous Hall effect (QAHE) [9]. Subsequently, in 2007, a team of researchers from Switzerland conducted a successful experimental verification of the QAHE, utilizing cadmium selenide (CdSe) films to construct the initial QAHE system [10]. Subsequently, the Quantum Anomalous Hall Effect (QAHE) has garnered significant attention within the fields of materials science and condensed matter physics as a prominent area of research. Researchers are actively engaged in the pursuit of novel materials and architectures that can facilitate the manifestation of QAHE at elevated temperatures. This endeavor aims to unlock the potential of QAHE in quantum computing and energy-related applications. The field of quantum anomalous Hall effect (QAHE) study continues to advance and expand through the collaborative endeavors of experimental investigations and theoretical analyses.

2. Overview

2.1. Brief overview of Hall Effect and its conventional and anomalous forms

The generation of a voltage differential in a conductor when an electric current travels through it perpendicular to a magnetic field is known as the Hall voltage phenomenon [11]. This phenomena is referred to as the Hall effect, as it is responsible for the production of the Hall voltage. The Hall effect is a well-known phenomenon that typically occurs in ferromagnetic materials [12]. When an electric current flows through a conductor, and the conductor is subjected to a magnetic field, the magnetic field exerts a force on the charge carriers. As a result, the charge carriers tend to accumulate on one side of the conductor, leading to an increase in charge density on that side and a decrease in charge density on the opposite side. The electric field created by this charge build-up equalizes the force exerted by the magnetic field on the carriers, creating a potential difference on both sides of the conductor, the Hall voltage [13].

The Hall effect in semiconductor materials can manifest in an aberrant manner [14]. In the context of semiconductors, the primary constituents of carriers are electrons and holes [15]. When a current flows through the semiconductor, the magnetic field applies transverse stresses on the electrons and holes, causing them to deviate laterally. Consequently, this leads to the accumulation of positive and negative charges on the sides. This accumulation creates an electric field such that a potential difference is created on the side, the Hall voltage [16]. The Hall effect has a wide range of applications in practical applications, such as measuring currents, magnetic fields, and speeds. By measuring the Hall voltage, physical quantities such as current, magnetic field, or the velocity of carriers can be calculated [17]. Since the Hall effect responds differently to different materials and conditions, the appropriate materials and structures can be selected to achieve the desired measurement as needed.

2.2. Basic principles of QAHE / QHEs and their connection

The Quantum Hall Effect (QHE) is a phenomenon characterized by a distinct discontinuity in resistance when electrons traverse a two-dimensional electronic system perpendicular to an externally applied magnetic field, resulting in what is known as Hall resistance [18]. Simultaneously, the transverse current induces a voltage that exhibits a quantifiable change, typically in integer multiples, so giving rise to the Hall voltage [19]. The transport behavior of electrons in the Quantum Hall Effect (QHE) does not precisely align with the classical understanding of electron degrees of freedom, as it incorporates the influence of quantum mechanics [20].

The observation of the quantum Hall effect shows that the Hall conductance takes the form of an integer multiple of the conductance quantum ( \( \frac{{e^{2}}}{h} \) ) [21], where e is the electron charge and h is Planck’s constant. This discovery is known as the Integer Quantum Hall Effect (IQHE), and its appearance suggests that the quantum Hall effect is related to the fine structure of quantum mechanics [22]. Under the action of a strong magnetic field, the movement of electrons in the material is limited, and the scattering process between electrons is suppressed due to the strong interaction between electrons, resulting in the so-called zero-long-distance coherence, which is an important reason why the quantum Hall effect is not affected by impurity scattering [23]. When exposed to high magnetic fields, two-dimensional electronic devices’ band structures simplify and discretize. This simplification excites or occupies a few energy levels. The Quantum Hall Effect (QHE) electron count closely correlates with energy level occupancy. Position-dependence in the band structure is critical to the generation of conductive quantum states and density distributions [24].

The quantum anomalous Hall effect (QAHE) theory quantizes Hall effects in zero magnetic fields. It differs from magnetic field-induced QHEs in mechanism and characteristics. The notion of Quantum Hall Effects (QHEs) without magnetic fields was proposed in 1988. Due to topological insulator advances, experimental verification required 25 years. Insulators are a new topological state [25]. A discretized version of the anomalous Hall effect has received attention in condensed matter physics. Even without a magnetic field, the quantum anomalous Hall effect creates a topological boundary state in the thin conductor due to its well-organized spin polarization and charge distribution. Therefore, Hall voltage can be generated without a magnetic field [26].

QAHE by nature needs to maintain a zero-drift charge transport state, which means that the flow of current in the material is not scattered and there is no accumulation or drift of charge. This enables stable Hall conductance independent of external conditions [27]. The number of conductances produced at zero magnetic field is an integer multiple of the charge quanta, which means that under certain conditions, the Hall conductance value used to describe conductance is an integer, called the Chern number, which is related to the topological properties of the material [28]. The majority of studies investigating the quantum anomalous Hall effect (QAHE) have been conducted at lower temperatures [29]. This choice is motivated by the fact that electron transport at low temperatures is less prone to impurities, thermal excitation, and scattering, hence facilitating the observation of the QAHE phenomenon.

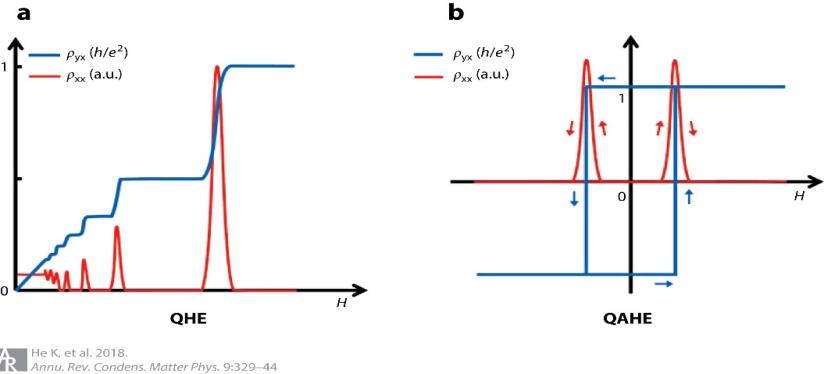
Figure 1. Schematic diagram of (a) QHE and (b) QAHE. The red and blue lines represent the magnetic field (H) dependence of the Hall resistance and the longitudinal resistance, respectively. The curve in Figure B represents the hysteresis caused by ferromagnetism, and the arrows represent the direction of the magnetic field scan [30].

3. Theoretical Foundations and Mechanisms of QAHE

3.1. Origin of topological edge states in QAHE

The origin of the topological edge state can be traced back to the early 1980s, when physicists discovered the quantum Hall effect, which is due to the existence of a special topology in the material, resulting in the movement of electrons forming a non-conductive energy level gap [31]. Subsequent studies have found that there is a close correlation between the bulk energy level structure of this quantum Hall effect and the boundary state energy level structure. Boundary states are quantum states that manifest at the periphery or interface of a material, and their emergence is safeguarded by topological characteristics, hence rendering them resistant to minor disturbances inflicted upon the material. In 1997, physicists discovered the first topological insulators, finding the existence of topological edge states in insulators. These edge states are very different from carrier behavior in traditional metals or insulators and have very specific properties: carrier behavior in traditional metals or insulators is determined by an energy band structure in which carriers can propagate freely inside the material. However, edge states are special electronic states in certain topological insulators or topological superconductors that occur at the boundaries or surfaces of these materials, rather than within the entire volume of the material [32].

3.2. Topological insulators and magnetic impurities in QAHE

Topological insulator is a novel material phase with topological invariance of band-to-band rebound in the electronic band structure. Unlike conventional insulators, it has an insulating state in the body, but at the same time there is a topological edge state on the surface that can conduct electricity. Topological insulators play an important role in the quantum anomalous Hall effect, and its conductance only relies on external magnetic fields under low temperature and strong magnetic field conditions without being affected by material impurities and is zero on the entire sample, but there are topological edge states that show extremely high conductance at the boundary, which is due to the existence of topological invariants to ensure that the edge states form an energy band in the energy gap, and the transmission of electrons in this energy band is scatter-free. Simultaneously, it is worth noting that topological insulators possess topological protection properties that effectively shield them from the impact of non-magnetic impurities on the Quantum Anomalous Hall Effect (QAHE). This protection arises from the presence of an energy gap in the topological edge state, which is a consequence of the topological protection mechanism. Consequently, non-magnetic impurities are unable to disrupt the topological nature of the system or alter the presence and robustness of the topological edge state. As a result, the conductance of the QAHE remains at a constant value of zero [33].

QAHE in topological insulators is also affected by the QHE and the quantum spin Hall effect, which are related to electron spin and spin-orbit coupling in topological insulators. The magnetic impurities present in QAHE have a spin magnetic moment, which can introduce a Stokes dipole in a two-dimensional gas, couple with electrons and obtain spin magnetization, causing the spin flipping of electrons, so that the spin-up and spin-down electrons are converted, thereby affecting their transmission characteristics and causing spin polarization and other effects [34]. By combining topological insulators with magnetic materials, spin-polarization currents can be generated, which are characterized by low energy consumption and high efficiency, and can be used in spin transport, spin logic, and spin storage.

3.3. Topological invariants and Chern numbers in the context of QAHE

In the context of QHE, topological invariants and Chern numbers are important concepts to describe topological properties. Topological invariants are mathematical quantities that can be used to characterize topological properties, and the most commonly used topological invariant in QAHE is the Chern number, which was introduced by physicist Chen Xingshen. The Chern number is a topological invariant that characterizes the topological properties of a two-dimensional electronic system. In the context of a two-dimensional material, it can be conceptualized as a lattice situated on a plane, where each lattice point corresponds to a specific position. The Chern number can be computed by performing an integration of the wave function over this lattice. Specifically, the Chern number is an integral of the Berry curvature over the entire First Brillouin Zone. Among them, Berry curvature describes the evolution of electrons in momentum space, which is related to the phase relationship between the wave functions of electrons, and by integrating Berry curvature, the Chern number can be obtained. It can be concluded that the Chern number with a non-zero value represents the topological non-triviality of the material, that is, there is a topological edge state in the material. At the same time, their non-zero value indicates the robustness of topological insulators under external disturbances, because the existence of their edge states is protected by topological properties, and this robustness is very important for applications in fields such as quantum computing and information storage [35].

3.4. Landau Levels and the quantization of Hall conductivity in the absence of magnetic field

Quantifying Hall conductivity at Landau levels and without magnetic fields is crucial in condensed matter physics. In two-dimensional electronic systems with a vertical magnetic field, electron energy levels are quantized into Landau levels, which are discrete states. These energy levels have a degenerate structure and correspond to a particular number of electrons whose energies depend on the magnetic field strength and electron density [36]. A Landau energy level feature defines the quantum anomalous Hall effect (QAHE). In particular, the energy band’s highest occupied Landau energy level has a non-zero Chern number without a magnetic field. Thus, a non-zero Chern number causes a non-zero Hall conductance, allowing charge separation and transport similar to the Hall effect without a magnetic field. This unique energy level structure is important for QAHE experimental and theoretical studies. The Landau energy level theory limits electron transport in magnetic fields to discrete energy levels called Landau orbitals. These energy levels depend on the external magnetic field and electron mass. As magnetic field strength increases, Landau energy levels are farther apart. This energy quantization theory underpins the quantum Hall effect. Quantization occurs in Hall conductivity without a magnetic field. Quantizing Hall conductivity means that its value is discrete and does not vary continuously without a magnetic field, similar to quantizing Landau energy level. Landau’s energy levels are distinct, hence the material has an energy gap where current can only flow along the boundary. Therefore, Hall conductivity quantization similar to the quantum Hall effect can still be observed in the absence of a magnetic field, which is of great significance for accurately measuring electronic behavior and material properties [37]. By employing theoretical simulation and experimental validation, we have derived a quantitative determination of the Landau energy level and Hall conductivity in the absence of a magnetic field. The theoretical simulation involves the utilization of established models in quantum mechanics and condensed matter physics, such as density functional theory (DFT), the tightly bound model, and the Kohn-Sham equation. These models, along with commonly employed numerical calculation methods, enable the computation of the Hall conductivity at the Landau energy level in the absence of a magnetic field. The experiment uses two-dimensional material samples, such as graphene, topological insulators, etc. to apply different magnetic field strengths, by measuring the conductivity and Hall resistance of the sample and its change with the magnetic field, observing the quantization phenomenon of Hall conductivity at Landau energy level and without magnetic field, and using valley analysis, spectral measurement and other technologies to deeply study and verify the specific mechanism of quantum effects.

3.5. Interaction effects and disorder in QAHE

The single-particle Landau level under an external magnetic field explains the quantum Hall state in the integer and fractional quantum Hall effect. In addition to the external magnetic field in QAHE, electron interaction affects the band structure and topological edge state, causing electron localization, Mott insulation state, and topological phase transition, as well as changing electron dynamic behavior and band structure [38, 39]. In some materials, interactions can cause spin polarization and electron ordering, affecting conductivity. The quantum anomalous Hall effect (QAHE) interaction also affects the topological edge state. This interaction adds inter-electron scattering and reflection processes, changing topological edge state electron transport. Thus, the contact might create, vanish, or reconfigure the topological edge state. An electron Fermi liquid is a common electron-electron correlation in quantum anomalous Hall effect (QAHE) systems. This state has spin-polarized electrons with strong correlations. Systems with significant Coulomb interactions and low electron concentrations show these relationships. QAHE emergence and stabilization depend on the coupling of the EF liquid to topological edge states [40-41]. The presence of disorder within a material, such as inhomogeneity, impurities, and defects, can give rise to a disorder-induced effect. For instance, in a topological insulator, the introduction of a berry phase can be achieved through the application of a magnetic field or spontaneous magnetism. When this phase undergoes a \( π \) change, it results in a non-trivial alteration in the band’s topology. This phenomenon, as observed in previous studies [42], typically disrupts the topological protection within the topological insulator and causes the loss of its topological properties. Therefore, it is imperative to minimize the occurrence of disorder in order to attain a more stable and reliable material for the Quantum Anomalous Hall Effect (QAHE). Localization caused by random magnetic field is a quantum effect in disordered systems, that is, in metals or semiconductors that do not require magnetic fields, electrons may be localized and their spins or orbits will be fixed by disordered magnetic fields, limiting the transmission of electrons and affecting physical properties such as conductivity and magnetic properties of materials. This localization effect is often associated with disorder-induced electron scattering and interference.

3.6. Role of spin-orbit coupling and time-reversal symmetry in QAHE

Spin-orbit coupling is a quantum mechanical phenomenon that describes the interaction between spin and orbital motion and plays an important role in QAHE. The phenomino introduces an interaction between spin and orbital motion, resulting in coupling between the direction of spin transport in the system and the direction of electron motion. This interaction can be regulated by magnetic fields and is related to the spin angular momentum and orbital angular momentum of electrons. In two-dimensional electronic systems, spin-orbit coupling can change the way electrons move, including changing the effective mass and band structure of electrons. This change causes a quantum jump in electrons under an external magnetic field and temperature, resulting in a quantum anomalous Hall effect. Spin-orbit coupling can achieve this effect by influencing the state density and scattering mechanism of electrons [43].

Time reversal symmetry states that physical processes and laws do not alter when time is reversed [44]. In quantum anomalous Hall effect (QAHE), time reversal symmetry ensures that electrons’ retrograde route has the same energy spectrum and structure. The dynamic equations governing electrons under time inversion are constant due to time inversion symmetry. The symmetric Hamiltonians describing the system give the QAHE certain properties. Time reversal symmetry guarantees boundary states in the quantum anomalous Hall effect, which is important to examine. The border state, a non-scattering condition at the perimeter of a two-dimensional electronic system, is important in the quantum anomalous Hall effect. Due to time reversal symmetry, the border state’s energy spectrum remains the same in positive and negative time, ensuring its existence and longevity. The conductive characteristics of the QAHE are also affected by time reversal symmetry. Time inversion symmetry distinguishes normal and anomalous Hall effects. In a time-inverse-symmetrical system, the Hall conductance is zero when the current flows through a two-dimensional electronic gas in one direction. In a time-inversion-altered system, the current goes through an anomalous Hall conductance. The quantum anomalous Hall effect’s topological features and conductance direction depend on time inversion symmetry.

4. Experimental Achievements and Discoveries

4.1. Milestones in the experimental realization of QAHE

The quantum repulsive effect was first observed experimentally in 2007 as a precursor to the quantum anomalous Hall effect, illustrating that spin-orbit coupling can cause topological energy gaps in two-dimensional electron gas. In 2013, a research team from Huazhong University of Science and Technology realized the quantum anomalous Hall effect of spontaneous magnetization for the first time in thin films, using lanthanum copper oxygen (La-Cu-O) thin films, and observed quantum anomalous Hall states with completely internal tricky states in the laboratory. In the same year, the research team of Stanford University successfully realized the spontaneous magnetization quantum anomalous Hall effect by introducing the ferromagnetic material bismuth antimony alloy to interact with the semiconductor periphery on a special ferromagnetic semiconductor quantum well. Then, in 2015, the research team at the University of Texas at Austin observed the quantum anomalous Hall effect in the topological insulator (TI) film, and they successfully achieved QAHE at low temperatures by coupling the TI film with ferromagnetic materials (such as ferromagnetic semiconductors, ferromagnetic metals, etc.) [45]. One year later, a group of researchers from Stanford University in the United States successfully demonstrated the occurrence of the QAHE at the interface between graphene and boron-nitrogen metal. They discovered this effect under highly reduced temperatures by utilizing the heterogeneous structure composed of graphene and boron nitride.

4.2. Observations of topological edge states in QAHE

The topological edge state refers to the special electronic state that exists at the edge or interface of the QAHE material, and its energy level distribution is significantly different from the posture. These edge states form energy level intervals in the band structure and are closely related to the topological properties of the material.

The presence of topological edge states holds significant implications and practical relevance in the context of the QAHE. The material boundary can generate an electron energy level without an energy gap, resulting in a distinct dispersion relationship in the energy spectrum. This implies that electrons can move freely across the boundary without being constrained by an energy gap, leading to high conductivity and low dissipation. Consequently, materials exhibiting the QAHE hold significant promise in the development of electronic devices and circuits. These materials have the potential to achieve low energy consumption, high speed, and high precision electron transport [46].

At the same time, the topological edge state also has very stable characteristics, because its existence is related to the topological invariant of the system, so it has certain protection under small changes in the local structure of the material. This means that even in the presence of defects or impurities, the topological edge state can still maintain its characteristics and transmission capacity, making QAHE materials anti-interference and noise tolerant, providing more reliable performance for practical applications.

4.3. Synthesis of QAHE materials and common materials

Materials with QAHE exhibit unique conductivity and can achieve zero resistance, making them ideal for low-power electronics, qubit construction, magnetic flux measurement, spin materials, and spin transport research. To achieve the QAHE, magnetic materials must be synthesized with high quality and purity. Researchers have developed many synthetic methods to modify magnetic material composition and structure. This includes molecular beam epitaxy, chemical vapor deposition, and solution-based techniques. These methods produce materials with precise architectures and compositions [47]. As mentioned, selecting and integrating magnetic impurities is crucial to QAHE, and it was quickly discovered that studying different magnetic impurities and adjusting parameters like concentration, shape, and distribution, as well as using materials engineering strategies like doping, interface effects, etc., was the key to successfully implementing and optimizing this material. Both the spatial organization, positional distribution, and mode of magnetic impurities inside the crystal lattice affect their creation and properties. Researchers can optimize magnetic impurity-electron interaction using lattice control. Choosing the appropriate crystallization direction and vertical stacking improves QAHE. The Stokes dipole magnetic field caused by magnetic impurities also affects the quantum anomalous Hall effect [48]. With the in-depth understanding of quantum anomalous Hall-effect mechanisms and the further development of material design concepts, some common QAHE materials that have been discovered so far include:

HgMnTe: Mercury-manganese-gallium tellurium is a composite material that combines the special structure of mercury-zinc tellurium and manganese tellurium. It can exhibit the QAHE effect at low temperatures and has a high Fermi level. Cr-doped (chromium-doped) topological insulators: Some topological insulator materials, such as topological insulators (Bi, Sb) 2Te3, can exhibit QAHE phenomenon at low temperatures after chromium (Cr) doping. V-doped (vanadium-doped) topological insulators: Similar to Cr doping, some topological insulator materials doped with vanadium (V) can also exhibit the QAHE effect.

In addition to the topological insulators mentioned above, some other topological insulator materials, such as HgTe quantum wells and Bi2Se3, can also implement QAHE under specific experimental conditions. At the same time, based on first principles and tight binding models, some scientists have also predicted a series of materials that are expected to achieve quantum anomalous Hall effects, such as Sn, CrP2S6, Cs2LiMn3F12, OsCl3, RuI3, PdBr3, V2O3, CrMnI6, chalcogenide-modified Pt2HgSe3, etc. [49-58].

Figure 2. The (a) Hall resistance and (b) longitudinal resistance were measured as magnetic field functions of different gate voltages in Cr-doped (Bi, Sb) 2Te3 films. Accurate quantification of Hall resistance and negligible longitudinal resistance at zero magnetic field was observed in 2Te3 films doped with (c)V and (d) Cr doped (Bi, Sb) [59].

5. Applications and Potential of QAHE

5.1. Quantum computing and information storage based on QAHE

The topological edge state of QAHE material has the characteristics of spin polarization and unique transmission channel, which makes it a powerful choice for constructing high-performance qubits [60]. The topological edge states of QAHE materials can provide long spin-coherent times, reducing error and noise, and enabling more complex quantum computing operations. Simultaneously, the presence of topological edge states in materials exhibiting the QAHE also gives rise to a non-local coupling effect. This effect enables the possibility of interaction between qubits and facilitates quantum gate operations. The interplay among qubits is of utmost importance in the execution of quantum algorithms and quantum information processing. The distinctive characteristics exhibited by materials exhibiting the QAHE offer novel avenues for realizing these operations. Furthermore, it should be noted that the topological edge states shown by materials with QAHE possess a remarkable resilience against noise and interference. This inherent property renders them very dependable for applications like quantum memory devices [61]. QAHE materials can be used to create high-capacity and high-stability quantum storage devices that effectively protect and transmit qubit information. By taking advantage of the special topological properties of QAHE materials, error correction and protection of qubits can also be realized, thereby improving the reliability and stability of quantum computing.

5.2. Energy conversion and spintronic applications of QAHE

QAHE-based energy conversion refers to the use of quantum anomalous Hall effect (QAHE) phenomena to convert one form of energy into another. QAHE is a quantum phenomenon observed at room temperature with low resistance and high efficiency, so it has potential applications in the field of energy conversion.

An important way to convert energy is thermoelectric energy conversion. Through the thermoelectric effect generated by QAHE, it can convert thermal energy directly into electricity. The generation of an electric field by the QAHE can efficiently transfer thermal energy into electricity when there is a temperature gradient in the material [62]. This application holds significant importance within the domains of energy management and heat usage. For instance, it has the potential to enhance the operational efficiency of thermal power generation apparatus and augment the energy usage efficacy of waste heat recovery systems.

Another application is photoelectric energy conversion. QAHE can convert light energy into electricity through the photoelectric effect. When light hits the surface of QAHE materials, the electric field generated by QAHE can convert light energy into electrical energy [63]. This provides a potential direction for the development of solar cells and optoelectronic devices. By using the photoelectric properties of QAHE materials, efficient light energy conversion can be achieved, thereby promoting the utilization of renewable energy and the performance improvement of optoelectronic devices.

5.3. Possible technological advancements enabled by QAHE

QAHE’s research has led to potential technological advances in many technical fields. In the energy sector, the application of QAHE helps to improve energy capture, storage and conversion efficiency, and the use of QAHE materials to recover energy from waste heat can improve energy efficiency and reduce energy waste. QAHE can also be applied to a variety of new energy devices, such as fuel cells and photovoltaic cells, to improve energy conversion efficiency while reducing dependence on traditional energy sources. In the field of information technology, QAHE information storage technology will also provide great potential for memory capacity and speed, and the memory built with QAHE materials can achieve higher density and faster data access, driving the development of big data, artificial intelligence and cloud computing. In addition, the unique properties of QAHE materials also make it possible for new security technologies, such as quantum teleportation and quantum encryption. In addition, in the field of materials science, the unique electronic structure and quantum properties of QAHE materials make them have various excellent physical properties, such as magnetic properties, topological insulation and nonlinear optical properties, which will promote the discovery and design of new materials and open up new functional materials fields. They are used in electronic devices, optoelectronic devices and quantum devices [64-66].

In addition, QAHE technology is expected to play an important role in many fields such as sensor technology, medical diagnostics, safety protection, spintronics, and topological photonics. Manufacturing high-sensitivity sensors from QAHE materials also enables more accurate detection and measurement, providing more reliable solutions for environmental inspection, biomedical and industrial monitoring, and more. Despite the challenges in its application and commercialization, through continuous research and development, we can foresee significant technological advances and innovations in emerging fields brought by QAHE technology to fields such as energy, information and materials science.

6. Conclusion

The examination of the quantum anomalous Hall effect uncovers significant phenomena and potential applications within the realm of condensed matter physics and materials science. Its primary revelation pertains to a novel comprehension of topological insulators and the topological states of matter, thereby highlighting the criticality of topological invariants and topologically protected states. The aforementioned discovery has stimulated additional investigation into topological phenomena and has yielded novel concepts and approaches for the creation of materials. QAHE has a significant impact on condensed matter physics and materials research through improving understanding of fundamental scientific principles, particularly in topological insulators and protective states. The QAHE research field offers innovative concepts and methods for materials design and investigation. It accelerates material research and development. Its potential uses in quantum electronics, quantum computing, and developing electronic devices have made it a popular research topic.

The QAHE has great potential for future research, including the study of topological protected states, the discovery of new materials with QAHE capabilities, and their use in quantum electronics and quantum computing. The issues also include the fabrication of high-quality and stable samples and the development of better QAHE control and regulation systems.