1. Introduction

Aerodynamics is vital in the never-ending quest for improvement of automotive performance and efficiency. The boundary between laminar and turbulent flows is marked by the Reynolds number. This boundary is important in determining how much aerodynamic drag a vehicle experiences.

Over the years, there has been a significant evolution in automotive design. Early cars pay little attention to aerodynamics because they are primarily concerned with functionality. However, the importance of streamlined designs becomes apparent as common knowledge of fluid dynamics expands and the demand for greater fuel efficiency and speed increases. Today, even regular cars are designed with a keen eye toward reducing air resistance, not just for high-performance race cars that place a high value on aerodynamic perfection.

The prominence of the Reynolds number is due to its ability to describe the airflow regime around a car. Depending on the Reynolds number, the flow can either flow laminarly and smoothly past the vehicle or turbulently and chaotically [1]. The complexities of this transition significantly impact a car’s performance metrics, ranging from top speed to fuel consumption.

This article explores the intricate connection between the Reynolds number, automotive design methods, and the resulting performance outcomes. This article aims to provide a holistic perspective on how the Reynolds number can be manipulated to optimize vehicular aerodynamics. This article will explore the next stage of automotive design through this investigation, where the fusion of form and fluid dynamics ushers in a period of unmatched performance and efficiency.

2. Reynolds Number and Aerodynamic Drag on Cars

2.1. Basic Concepts and Definitions

The Reynolds number, as shown in Equation 1 [2], is a dimensionless number used to measure the fluid regime. It bears the name of Osbourne Reynolds, who conducted research on the transition of laminar and turbulent flow in testing pipes. The fluid is classified as being in turbulent, laminar, or transitional flow based on its Reynolds number. The flow pattern is based on Reynolds number. The most frequent flow pattern in real life is turbulent because most real objects, like cars and airplanes, are very large in scale. As a result, the characteristic length will also be very large, resulting in a very high Reynolds number.

\( Re=\frac{ρvL}{μ}\ \ \ (1) \)

where ‘ρ’ stands for flow density, ‘v’ for fluid velocity, ‘L’ for pipe or tunnel length, and ‘μ’ for dynamic viscosity.

2.2. Impact on Fuel Efficiency and Performance

From the perspective of optimizing the car’s fuel economy, drag is an irreplaceable factor in determining the behavior of a road vehicle. The boundary layer will change from a laminar to a turbulent boundary layer if the speed increases or the length of the car’s surface increases. Due to the features of turbulent flow, the fluid mixes and oscillates. It brings faster turbulence to the surface, which significantly increases skin friction. By analyzing experimental data, the pressure drag is proportional to the speed of a car [3]. In practice, skin friction results in drag. So, the smoother the surface of a car is, the better fuel efficiency will be.

3. Comparative Analysis of Different Car Designs

A car’s shape and design modifications are crucial in determining how it interacts with the surrounding air. Understanding how various designs navigate the difficulties and opportunities of fluid dynamics becomes essential when the Reynolds number is used as the guiding metric.

3.1. Shapes and Models

The complexity of the field of vehicular aerodynamics necessitates a delicate blending of art and empirical science. In this dynamic interplay, it is impossible to overstate the importance of the Reynolds number—a crucial parameter illuminating the nature of fluid flow.

Sedans perfectly illustrate the fine line between aerodynamic effectiveness and aesthetic elegance. Their extended chassis and sleek profiles are carefully engineered to handle the challenges presented by varying Reynolds numbers. In addition to being an aesthetic marvel, the tapering rear is characterized by its capacity to preserve laminar flow regimes and reduce the emergence of turbulent eddies that increase drag, particularly as Reynolds numbers increase [4].

A detailed look into racing vehicles’ aerodynamics indicates an active struggle against the emergence of turbulence. Reduced height and increased breadth of the vehicle are intended to alter flow characteristics at a particular Reynolds number. With slanted roofs and curved sides, they purposefully delay flow separation at higher speeds (and consequently high Reynolds numbers), maintaining laminar flow regimes and reducing drag [5].

Due to their large frontal areas and sturdy construction, trucks and sport utility vehicles(SUV) naturally operate in domains with higher Reynolds numbers. They are more vulnerable to turbulent flow regimes as a result. Innovations like aerodynamically optimized wheel arches and grille designs have been made to manage and traverse the difficulties brought by higher Reynolds numbers.

3.2. Design Modifications

Modern vehicle adornments conceal sophisticated aerodynamic strategies beneath their outward appearance, many of which are inextricably linked to controlling flow regimes determined by the Reynolds number. The subtleties of automotive design, are firmly rooted in the empirical field of fluid dynamics. Every contour and curve provide a solution to the problems that are brought by the different Reynolds numbers.

The Spoiler’s function goes beyond its aesthetic value. The onset of turbulence is inevitable at high speeds, where Reynolds numbers soar. Figure 1 shows that the principle of Spoilers is strategically positioned to spoil the turbulence, decreasing lift, reducing associated drag, ensuring that the flow remains attached for longer, and lowering the adequate Reynolds number local to the back of the vehicle [6].

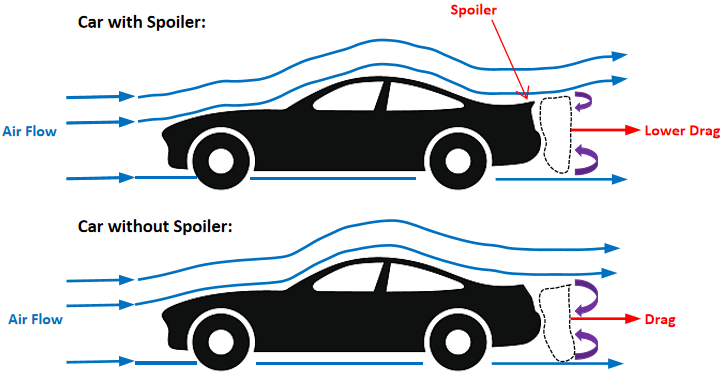
Figure 1. Comparison of cars with or without spoilers.

Diffusers are masters at controlling high Reynolds number flow dynamics. Diffusers work to reduce low-pressure zones that otherwise cause drag.

Vortex Generators are not haphazard additions. They aim to create controlled vortices, especially in areas where flow separation is a concern due to the local Reynolds number. These generators ensure flow adhesion by energizing the boundary layer, which reduces the drag brought on by flow separation at high Reynolds numbers [7].

4. Influence of Surface Roughness

The texture or inconsistencies of a solid surface are referred to as surface roughness. These abnormalities include macroscale structures like protrusions and depressions or microscale characteristics like bumps and grooves. Surface roughness affects the creation and behavior of boundary layers and the fluid’s ability to flow smoothly. The fluid experiences local flow velocity, pressure, and shear stress fluctuations as it passes over a rough surface.

The aerodynamic resistance to fluid contact on an object’s surface is known as surface friction. The boundary layer frequently goes hand in hand with skin friction. When a fluid moves in relation to an object, the boundary layer is produced. As the fluid passes the object, the molecules immediately above the surface interact with the surface more slowly. The molecules above them become slower, forming a thin layer of fluid that touches the surface. From zero at the outermost layer to the free stream value farther away, the velocity varies in this area. The boundary layer may be laminar, turbulent, or a combination of the two if the object is long and there is a transition between the two. There is the greatest amount of flow separation in turbulent flow. As a result of flow separation, eddies and vortices form downstream of the object, causing a larger wake region and an area of low pressure, which increases drag forces.

With rough surfaces, all the characteristics above are amplified. A rougher surface increases the area in contact with the fluid, creating a more turbulent boundary layer with the same Reynolds number. It has also been shown that with increasing roughness, the transcritical drag coefficient rises while the critical Reynolds number lowers[8]. The critical Reynolds number is the number that, when surpassed, generates turbulent flow. Hence, a lower critical Reynolds number means that turbulent flow and turbulent boundary layer occur more often, resulting in more drag. Although surface roughness has little impact on drag, it lowers the critical Reynolds number, which causes an earlier transition to the critical area [9]. Hence, the vehicle will be less fuel efficient and have higher drag with a rougher surface.

5. Ground Effect and Active Aerodynamics

It is well known that ground effect aerodynamics is widely used in the design of racing cars. Ground effect is the most efficient part of aerodynamics in race car design. It can significantly increase downforce without introducing much drag and plays a significant role in reducing lap times.

Active aerodynamics works by utilizing adjustable components on the vehicle to change the external shape and wind resistance. These adjustable parts typically include front lips, rear spoilers, rear wings, etc. By adjusting the position and angle of these parts, the external shape of the vehicle can be changed, thus realizing active control of the vehicle’s aerodynamic performance.

5.1. Importance in Racing and Performance Cars

A set of wind tunnel tests at the University of Southampton helps understand the aerodynamic factors that influence the aerodynamics of racing and performance cars when overtaking. A ground-effect wing underneath a body containing a diffuser and a rear wing has been tested to get typical data on what happens when one race car follows another. The results are compared to baseline data obtained without the presence of the car body. The amount of the downforce loss is found to depend on the height of the airfoil above the ground and to decrease behind the upstream hull. Additionally, it is demonstrated that downforce is lost more quickly near the airfoil’s center than it is near its wingtips. Therefore, a racing car can raise the airfoil to reduce air resistance on a straightaway and drop the airfoil in turn to increase downforce and take the turn at a faster speed [10].

In addition to improving handling, active aerodynamics raises a racing vehicular aerodynamic efficiency. Swift vehicles’ lateral stability in tight turns can be effectively improved by active aerodynamic management. The vehicle’s lateral stability can be ensured by obtaining a favorable transverse moment by varying the angle of attack that are impacted by the right and left split rear wing [11].

5.2. Active Aerodynamic Features and Real-time Manipulations

The Mitsubishi HSR II, a concept car unveiled at the 1989 Tokyo Motor Show, has movable aerodynamic features like a chin spoiler, rear lower flaps, and two pairs of duck wings and rear flaps, for instance. These components are intended to support acceleration, cornering, and braking actions. The vehicle experiences a 0.21 increase in drag and a 0.42 decrease in lift coefficient as a result of active aerodynamic components that enhance braking [12].

Although the active aerodynamic element’s surface area is crucial, the way the element interacts with the rest of the body is also crucial. Additional aerodynamic forces can be obtained from the element itself if it is positioned properly. Cars, however, are only able to accommodate a certain number of these components. If not, the airflow might completely separate from the body, rendering all of the equipment in the wake stream useless.

6. Cooling Systems

The thermal management system or the cooling system, is one of the most neglected but essential factors in a vehicle’s performance. Effective cooling affects many ancillary systems, including turbochargers and battery cooling in electric vehicles, and ensures the best engine performance [13]. The Reynolds number plays a very subtle and complex role in this situation.

Depending on the Reynolds number, fluid flow in cooling ducts and radiator channels can be classified as laminar or turbulent. Convective heat transfer coefficients are typically increased in turbulent flow, which is made possible by a higher Reynolds number. As a result, automobiles with cooling systems built for higher Reynolds numbers are frequently better at dissipating heat.

The Reynolds number also influences the formation of a boundary layer along the cooling fins and the bulk fluid flow. A higher Reynolds number often improves the overall rate of heat transfer because a thinner thermal boundary layer is produced more frequently [14]. Given these dynamics, automotive engineers regularly employ computational fluid dynamics (CFD) simulations to optimize the flow pathways, duct geometries, and even fin designs by modifying the Reynolds numbers.

7. Conclusion

This article has clarified the intricate connection between automotive aerodynamics and the Reynolds number. The Reynolds number emerges as a crucial tool for optimization, from evaluating different car shapes to analyzing particular design modifications like spoilers and diffusers. It has been found that changing the Reynolds number significantly impacts the drag forces. In addition, cooling systems, a crucial but frequently disregarded aspect of vehicle performance, are affected by Reynolds Number. Engineers can create more effective and efficient cooling systems by understanding how the Reynolds number affects heat transfer coefficients and boundary layer dynamics.

In conclusion, this article provides a comprehensive understanding of the function of Reynolds numbers in automotive design.

Authors Contribution

All the authors contributed equally and their names were listed in alphabetical order.