1.Introduction

In the domain of cryptography, the RSA and Elgamal algorithms stand as two timeless classics. The RSA algorithm, an acronym derived from the surnames of its inventors - Rivest, Shamir, and Adleman - is the oldest and most prevalent public-key cryptosystem. Introduced to the public in 1977 [1], the RSA hinges on a user's ability to generate and publish a public key rooted in two large prime numbers, combined with an auxiliary value. Its robust security is anchored in the "factoring problem" - the tangible challenge of decomposing a large number into the product of two prime constituents. To date, this problem remains unsolved by any established method.

On the other hand, the Elgamal algorithm, birthed by Taher Elgamal in 1985, offers an asymmetric key encryption tailored for public-key cryptography. Typically operating within a cyclic group, its common application involves the multiplicative group of integers modulo n. The algorithm's security rests on the discrete logarithm problem [2]. Any interloper seeking to decrypt a message faces the daunting task of resolving a discrete logarithm modular equation featuring exceedingly large numbers - a challenge that has proven arduous. With prevalent programming languages like Python and C++, encrypting information has become more accessible than ever. However, the pressing question remains: given similar algorithmic security levels, which combination of encryption algorithm and programming language offers the swiftest efficiency? This article embarks on a comparative journey to pinpoint the most effective pairing.

2.Mathematical Foundations

RSA algorithm: In the beginning of the RSA logarithm, the first step is to generate the key. Choose two large prime numbers, called them p and q. They should satisfy that they are both very large, and also their difference should be very large as well. Usually, in the algorithm, the prime numbers are chosen based on primality test until they are finally found. p and q ought to be kept secret within the key holder. Then one can compute the first part of the public key, n, such that.

\( n=p*q\ \ \ (1) \)

and it should be released to the public. Then is to generate the Euler’s totient function, called φ(x), for n [3].

The definition for φ(x):

\( n*(1-\frac{1}{p1})*(1-\frac{1}{p2})*…*(1-\frac{1}{pr})\ \ \ (2) \)

where pi is distinct prime factors of x.

This is kept secret as well. Since p and q are both prime numbers, it can be computed in the following way:

\( φ(n)=φ(p*q)=φ(p)*φ(q)=(p-1)*(q-1)\ \ \ (3) \)

The auxiliary value, call it e, is chosen based on the range from 2 to the value of the previous Euler’s totient function, namely:

\( 2 \lt e \lt φ(n)=(p-1)*(q-1)\ \ \ (4) \)

It should also be coprime to that function’s value, that is,

\( gcd{(e, φ(n))}=1\ \ \ (5) \)

The value of e is released as the second part of the public key.

The final stage of generating the key is to determine the modular multiplicative inverse of e modulo φ(n), call it d. So, d satisfy the modular equation.

\( de≡1(modφ(n))\ \ \ (6) \)

Or,

\( d≡{e^{-1}}(modφ(n))\ \ \ (7) \)

The value for d is kept secret. Note that, in practical, the modular multiplicative inverse can be computed by using the extended Euclidean algorithm efficiently.

Now suppose that B wants to send message to A and wants to encrypt it: B must know the public key of A, and also A must use his own private key to decrypt that message. That is, if using the symbol previously, A transmits the public key pair (n, e) to B and keep his private key d secretly. After receiving the pair (n, e), B can send his message, call it M, to A. Assume M is a plain text. The first step is to convert the plaintext into an integer m, called padded plain text, such that.

\( 0≤m \lt n\ \ \ (8) \)

Then the cypher text c is computed using the public key of A, namely n and e, such that.

\( c≡{m^{e}}(modn)\ \ \ (9) \)

Since c is calculated in the modular form, this computation will not be difficult. Then B can transmit his cypher text c to A. Eventually, A can decrypt the message using following way:

\( {c^{d}}≡{(〖{m^{e}})〗^{d}}≡m(modn)\ \ \ (10) \)

And the whole process for RSA algorithm is done.

Elgamal algorithm:

Firstly, the Elgamal algorithm is based on a cyclic group (which called G in the following parts). Cyclic group is generating based on its subgroup. Assume that g is any element in group G. Define the subgroup for g as following:

\( 〈g〉=\lbrace g\text{^}k|k∈Z\rbrace \ \ \ (11) \)

Formally, it is called the cyclic subgroup generated by g. The order of the subgroup g, |g|, is defined as the number of elements in the subgroup by g. The cyclic group is the group which is equal to one of its cyclic subgroups for some element g (called the generator of G). That is,

\( G=⟨g⟩=e,{g^{1}},{g^{2}},…,{g^{n-1}}\ \ \ (12) \)

In the following text, we define the group G has order q and is generated by the generator g [4].

Similar to RSA algorithm, the first step is to generate a public key pair, and also the private key. Suppose also B wants to transmit message to A. Firstly, A should determine the group G and also q and g. The auxiliary value, call it x, is chosen randomly from the set\( \lbrace 1,2,…,q-1\rbrace . \)

Then the value of the x-th exponent over g is computed as a part of the public key, that is

\( h={g^{x}}\ \ \ (13) \)

Then the public key pair from A is (G, q, g, h) and they are transmitted to B. x is retained secretly by A as his private key [5].

The second part is the encryption by B. Also call the message to be M; After converting the plain text M to the padded plain text m, B shall first map his message m to an element m of G using the reversible mapping function. In brief, if m is less than q, then map m to the m-th element in the group; but if m is greater or equal than q, then B should divide m into blocks such that the block size is one bit less than the bit size for q. Then B can map the message blocks into the group. B then choose an integer y similarly as the process for determining x: y is an integer randomly from the set\( \lbrace 1,2,…,q-1\rbrace . \)Formally, y is called the ephemeral key.

B also has to compute the shared secret for sharing with A, such that

\( s={h^{y}}\ \ \ (14) \)

The cipher text pair (c1, c2) is generating as following:

\( {c_{1}}={g^{y}}\ \ \ (15) \)

\( {c_{2}}=m*s\ \ \ (16) \)

After computing them, the pair (c1, c2) is sent to A.

A can then decrypting the message pair following these steps [6,7]:

Firstly, A also compute s, but in a different way, namely using her own private key x:

\( s={{c_{1}}^{x}}\ \ \ (17) \)

This is valid since it is known that

\( {{s(A)=c_{1}}^{x}}={({g^{y}})^{x}}={({g^{x}})^{y}}={h^{y}}=s(B)\ \ \ (18) \)

Secondly, A will compute the inverse for s in the group G.

\( {s^{-1}}={{c_{1}}^{q-x}}\ \ \ (19) \)

This is also valid since it is known that

\( s*c_{1}^{q-x}=({g^{xy}})*({g^{(q-x)*y}})={({g^{q}})^{y}}={e^{y}}=e\ \ \ (20) \)

Finally, B can decrypt the message m as following:

\( m={c_{2}}*{s^{-1}}\ \ \ (21) \)

since we know c2=m*s. Then B can map m back to the plain text M. And the algorithm is done.

3.Implementation

In this article, the programming software are Python Idle Shell 3.11.4 and C++ online in the Lightly project. The logic of the code is very simple; As encryption algorithms rely on mathematics and do not involve complex algorithms, the basic idea of these codes is basically consistent with the mathematical derivation in the second part. Roughly speaking, it is to first use a program to define some basic mathematical quantities (such as extended Euclidean algorithm), and then carry out basic programming in the order of information encryption and decryption, combined with mathematical formulas. In order to prevent the impact of the code itself on program runtime, the overall operation and algorithm of the code are basically consistent [8]. In addition, in order to exclude the influence of other irrelevant variables, the plain text of all information that needs to be encrypted in the program is set to the sentence "My name is Michael" to ensure the reliability of the conclusion to the greatest extent possible [9]. It is worth noting that in this article, there is a deficiency in the two large prime numbers p and q required for the RSA algorithm. Due to the load problem of the laptop CPU, too large prime numbers cannot be run out [10]. Therefore, the prime pair (p, q) selected in this article is (181,281).

4.Empirical Testing and Data Generation

After coding these algorithms, run these codes separately in different software. Each code is repeatedly run 30 times, and the overall running time of these programs is recorded in milliseconds each time.

The first combination is to use Python IDLE to run the RSA algorithm. As illustrating in the table 1, these 30 groups of data show the total running time of the algorithm, in millisecond:

Table 1. Experiment values for RSA algorithm in Python; unit: milliseconds (ms).

These data have a relatively big range, ranging from the minimum value of 254.2 ms to the maximum value of 743.2 ms, as shown in the Table 2. Their standard deviation also corresponds to this conclusion: with a large value of 144.5, the degree of dispersion of data is very high. This means that the fluctuation level for the running time is very high, the time range is relatively uncertain, as visualizing in the Table 2.

Table 2. Relative characteristic data.

Also, the average is slightly less than their median. An assumption can be made that the distribution for this combination is a left skewed distribution. As shown in Figure 1.

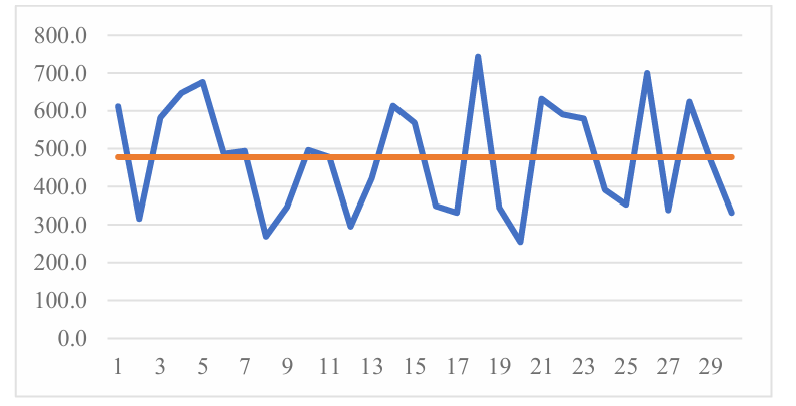
Figure 1. Average value (Photo/Picture credit: Original).

The second combination is to use Python IDLE to run the Elgamal algorithm. As illustrating in the table 3, these 30 groups of data show the total running time of the algorithm, in millisecond:

Table 3. Experiment values for RSA algorithm in Python; unit: milliseconds (ms).

These data values do not vary much, as shown in Table 3, the minimum time is 297.1 ms and the maximum time is 387.4 ms. Another advantage for this combination is their significantly low standard deviation, with only 22.5. This point is reflecting in the line chart in Table 4: all the data are very close to the average with tiny fluctuations.

Table 4. Relative characteristic data.

Also, the average is slightly more than their median. An assumption can be made that the distribution for this combination is a right skewed distribution. As shown in Figure 2.

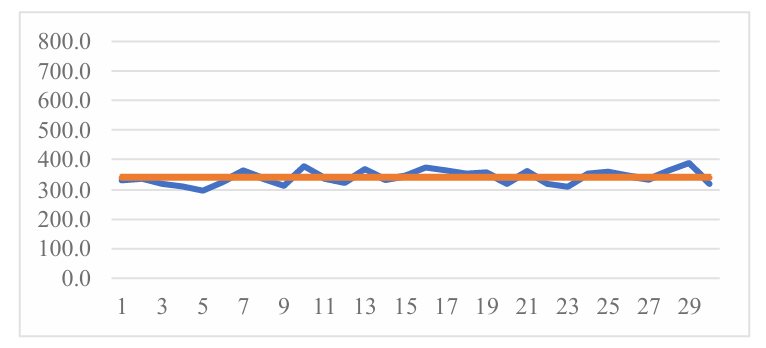
Figure 2. Compare average value (Photo/Picture credit: Original).

The third combination is to use C++ to run the RSA algorithm. As illustrating in the table 5, these 30 groups of data show the total running time of the algorithm, in millisecond:

Table 5. Experiment values for RSA algorithm in C++; unit: milliseconds (ms).

These data are relatively large, meaning that the time required to run the third combination will be longer. In Table 6, it is know that the minimum time is 1395 ms and the maximum time is 2781 ms, with a significance difference of 1386 ms. The standard deviation is also very high, of 281.2, implying a huge fluctuations of the data around their average, as visualizing in Table 6.

Table 6. Relative characteristic data.

Also, the average is slightly more than their median. An assumption can be made that the distribution for this combination is a right skewed distribution. As shown in Figure 3.

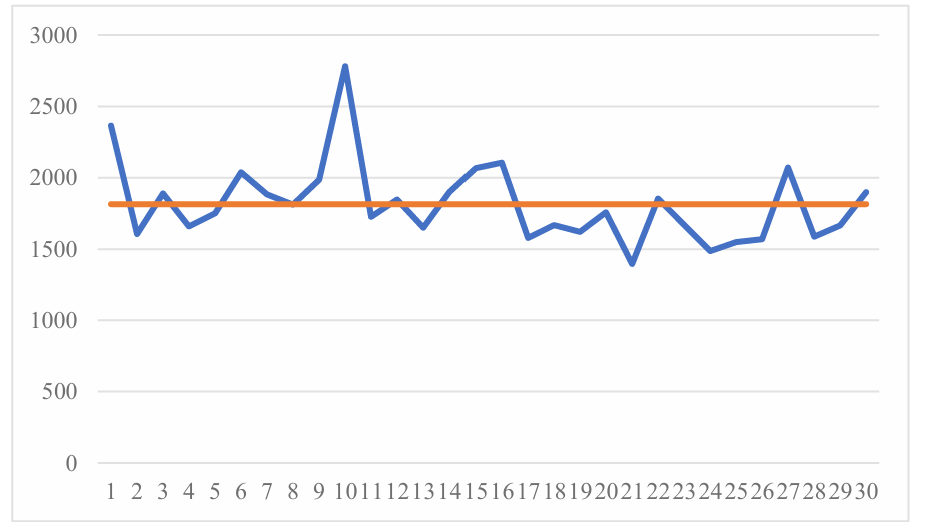
Figure 3. Compare average value (Photo/Picture credit: Original).

5.Data Analysis and Interpretation

The first comparison group is the combination one and the combination two. As shown in Figure 4.

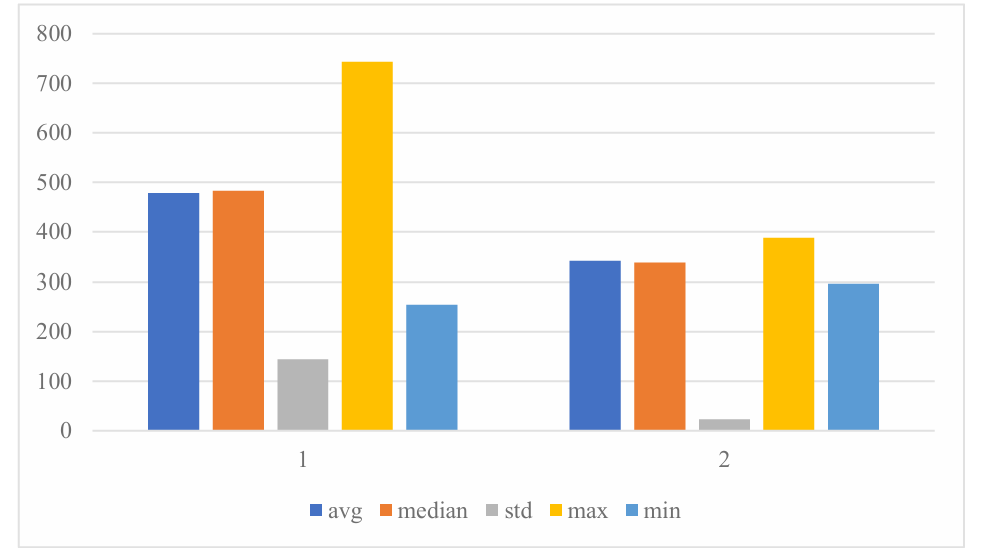
Figure 4. Comparison of combination 1 and combination 2 (Photo/Picture credit: Original).

It is clear that the average time used to run the algorithm for combination two is lower, which is 341.1 compare to 477.9 in combination one. Also, the data range for the second combination is much smaller than the other: the difference in time between their maximum value and their minimum value is 90.3 and 489.0 respectively. Combination1 has a range nearly 5.4 as much as the range for combination 1; correspondingly, the standard deviation for combination 1 and 2 is 144.5 and 22.5 respectively, with combination 1 almost 6.5 times bigger than that in combination 2. All this information shows much greater fluctuation and more time used for combination 1 compare to combination 2. This information is visualizing in Figure 5.

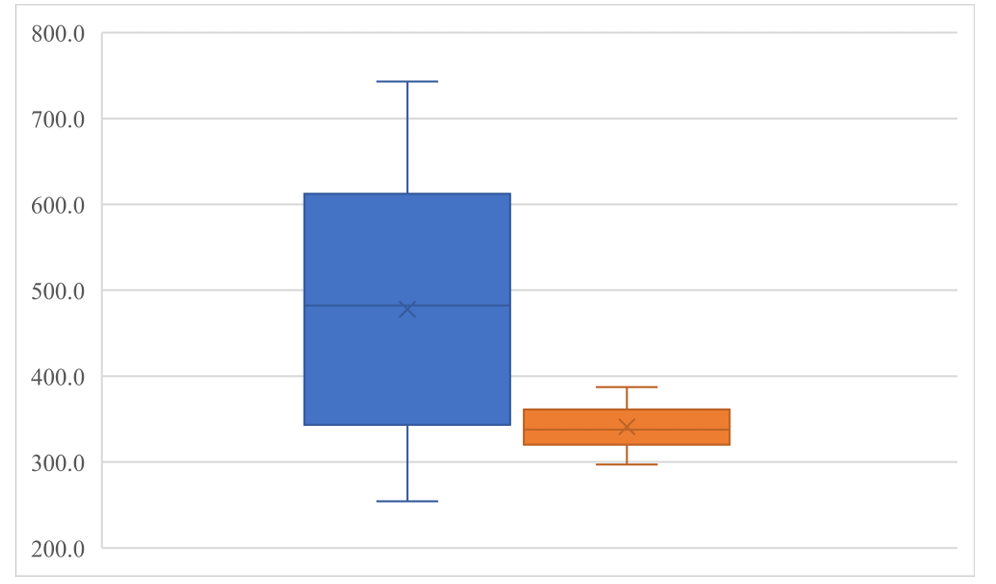
Figure 5. Comparison of combination 1 and combination 3 (Photo/Picture credit: Original).

The second comparison group is the combination one and the combination three. As shown in Figure 6.

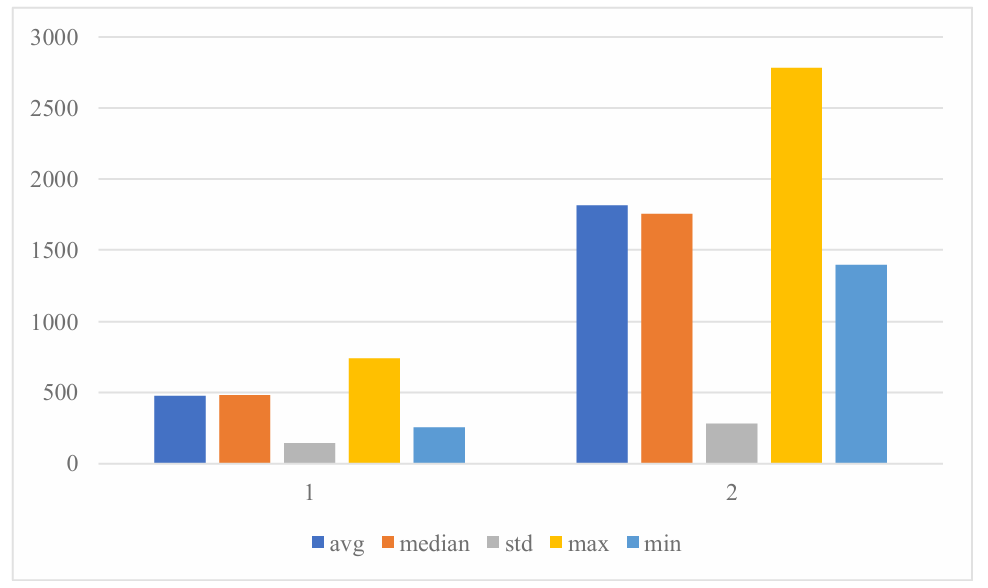
Figure 6. Box and whisker graph for comparing combination 1 and combination 2 (Photo/Picture credit: Original).

The differences between these data are very obvious. Every character value for combination 3 are significantly higher than combination 1. In terms of average, for example, is 477.9 and 1814 respectively, and the average time used for combination 1 is merely 26.3% of that in combination 3. The differences for minimum and maximum are also very huge: 1140.8 for the minimum value and 2037.8 for the maximum value. The standard deviation for combination 3 nearly doubled compare to combination1, meaning that it also has a larger fluctuation for the time cost to run the algorithm. These characters can be vividly seen in Figure 7.

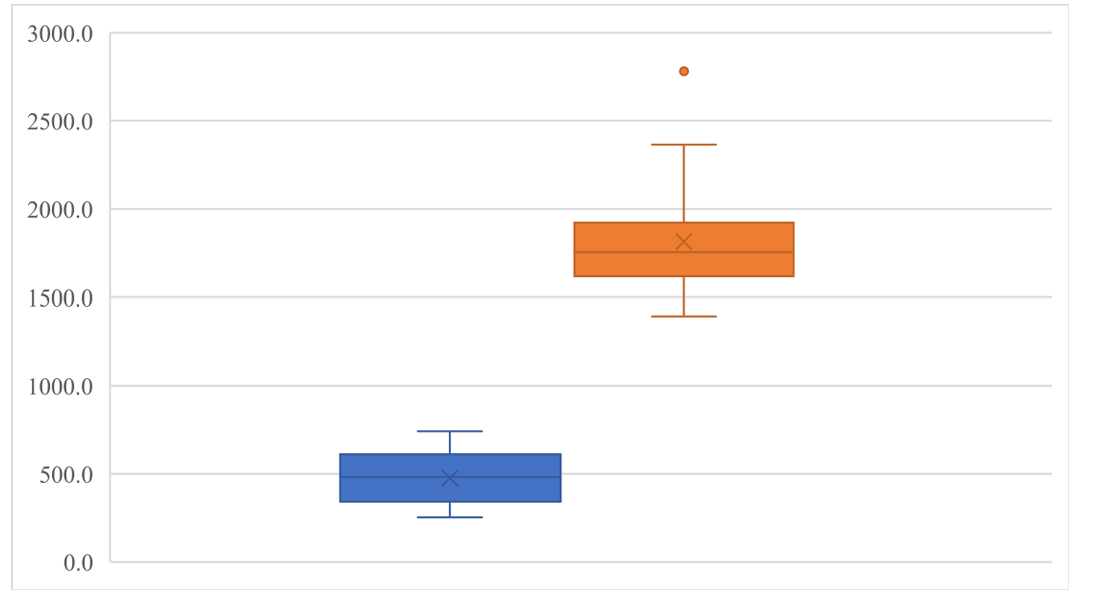
Figure 7. Box and whisker graph for comparing combination 1 and combination 3 (Photo/Picture credit: Original).

6.Conclusions

Upon careful examination of the two comparisons detailed in the fifth section, several conclusions emerge: Firstly, from comparison 1 between combinations 1 and 2, where the variable is the algorithm choice (RSA versus Elgamal) while holding the programming language constant (Python3), it's evident that combination 2 outperforms combination 1. This superiority holds true even when combination 1's runtime was adjusted for specific laptop performance considerations. Combination 2 boasts a shorter average and maximum runtime for the algorithm. Furthermore, a smaller standard deviation indicates more consistent runtimes across trials. Thus, the Elgamal algorithm demonstrates greater efficiency in message encryption and decryption compared to the RSA algorithm. Secondly, drawing from comparison 2 between combinations 1 and 3, where the variable is the programming language (Python3 IDLE versus C++), but the encryption algorithm (RSA) remains constant, combination 1 shows clear advantages over combination 3. The disparity in characteristic values is quite pronounced. Combination 1 consistently registers shorter average and maximum runtimes and a significantly lower standard deviation. This suggests Python3 IDLE outpaces C++ in terms of efficiency for message encryption and decryption tasks. In synthesizing the findings from both comparisons, it's discernible that combination 1 - employing the Elgamal algorithm in Python3 IDLE - offers optimal performance and efficiency in message encryption and decryption. For those seeking straightforward encryption for message dispatch on a laptop, employing Python with the RSA algorithm is recommended. Furthermore, it's plausible to extrapolate that beyond simple message handling, these conclusions may extend to broader scenarios involving extensive professional information encryption, transmission, and decryption. In such contexts, the Elgamal algorithm is likely to deliver superior performance and heightened average efficiency.