1. Introduction

At the dawn of the twentieth century, quantum theory was firmly established by scientists, allowing it to advance rapidly. Quantum tunnelling effect, a unique characteristic and fundamental quantum effect in quantum mechanics, is indispensable in numerous Physics processes. Exploring quantum mechanics, the Schrodinger equation furnishes a physical basis for elucidating the motion law of microscopic particles. This, combined with the theoretical investigation of electron tunnelling and the fact that numerous particles traverse the barrier, has made the electron transport phenomenon more widely known [1]. The probability of a particle passing through a barrier and appearing in the area behind it, regardless of its energy, is what is known as quantum penetration. Even when the barrier’s height is slightly lower than the particle’s energy, there is still a chance that it will reflect off its surface.

Hitherto, people must rely upon quantum mechanics, for classical mechanics is inadequate to explain these phenomena. The core of quantum mechanics is that particles possess wave-particle duality, and quantum tunnelling serves as the foundation for microcosmic particles to possess wave. It can also be used to explain tunnel diodes, cold emission of metal electrons, semiconductor p-n junction, decay of radioactive element a, thermonuclear fusion, etc. It can be applied to many different technologies, such as scanning tunnelling microscopy and programming floating gates, tunnel diodes for flash memory [2]. The Josephson effect, a common utilization of quantum tunnelling, is seen between superconducting or superfluid systems that are weakly coupled, where the current between them can be altered by the relative phase and tunnelling probability. This effect has some practical applications, such as in quantum biology, where electron penetration in enzyme catalysis and biochemical redox reactions is crucial. Quantum tunnels can also be used to measure magnetic fields and voltages with high precision, as well as superconducting qubits for quantum computers. Moreover, proton tunnelling is also associated with spontaneous DNA mutations [3].

The aim of this work is to illustrate the tunnelling effect in a double barrier and discuss the calculation of its transmittance. For this purpose, Section 2 reviews the single barrier module and discusses the double barrier tunnelling effect. The application of the tunnelling effect is introduced in Section 3.

2. Models of Potential Barriers

2.1. Brief review on single potential barrier model

To better understand the double potential barrier, this article will briefly review the tunnelling effect of a one-dimensional single potential barrier. The potential energy function of a single potential barrier shown in Figure 1 is illustrated as [4]

\( V(x)=\begin{cases} \begin{array}{c} {V_{0}}, 0 \lt x \lt L \\ 0, x \lt 0,x \gt L \end{array} \end{cases}.\ \ \ (1) \)

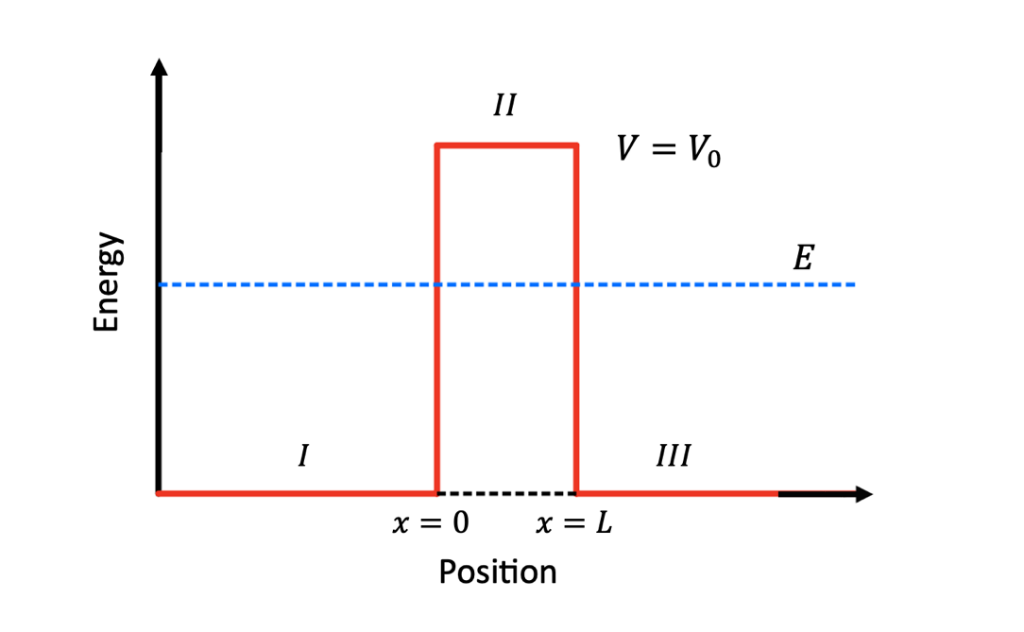
Figure 1. Single potential barrier model. \( E \) is the energy of particle energy, \( V \) is the potential energy of barriers, and \( x \) is the position.

For tunnelling effect this article will focus on \( E \lt {V_{0}} \) . When the particle energy less than the barrier potential energy, the boundaries of the barrier have probability to reflect the particle back. But in quantum mechanics, it also has probability through the barrier, which is impossible in classical physics. Start with the time-independent Schrödinger equation for one-dimensional system [5]

\( -\frac{ℏ}{2m}\frac{{d^{2}}ψ(x)}{d{x^{2}}}+V(x)ψ(x)=Eψ(x) \ \ \ (2) \)

Here, \( ψ(x) \) is the wave function, \( m \) is the mass of the particle, \( V(x) \) is the potential, \( ℏ \) is the reduced Plank constant, and \( E \) is the energy of the particle.

Next, the authors try to find the general solutions in each region [6]

\( \begin{cases} \begin{array}{c} {ψ_{I}}(x)={A_{0}}{e^{+ikx}}+A{e^{-ikx}} \\ {ψ_{I}}(x)={A_{0}}{e^{+ikx}}+A{e^{-ikx}}\ \ \ \ \ \ \\ {ψ_{III}}(x)=D{e^{+ikx}} \end{array} \end{cases}\ \ \ (3) \)

in which \( k=\frac{\sqrt[]{2mE}}{ℏ} \) and \( α=\frac{\sqrt[]{2m({V_{0}}-E)}}{ℏ} \) .To find out the coefficients in Eq. (3), authors use the boundary conditions for both sides to ensure that the wave function \( ψ(x) \) and its first derivative \( \frac{dψ(x)}{dx} \) across the boundaries continuously. At \( x=0 \) , it is found that

\( \begin{cases} \begin{array}{c} {A_{0}}+A=B+C \\ ik{A_{0}}-ikA=-αB+αC \end{array} \end{cases}.\ \ \ (4) \)

Similarly, at \( x=L \) :

\( \begin{cases} \begin{array}{c} D{e^{ikL}}= B{e^{-αL}}+C{e^{+αL}} \\ ikD{e^{ikL}}=-αB{e^{-αL}}+αC{e^{+αL}} \end{array} \end{cases}\ \ \ (5) \)

After solving the boundary conditions, one should find the ratio of the transmitted current to the incident current, which it is can be expressed in term of \( {A_{0}} \) and \( D \) . Namely,

\( T={|\frac{D}{{A_{0}}}|^{2}}=\frac{-16{k^{2}}{α^{2}}}{{[{(α+ik)^{2}}{e^{-αL}}-{(α-ik)^{2}}{e^{αL}}]^{2}}{e^{2ikL}}}\ \ \ (6) \)

Moreover, consider a “thick” barrier where \( αL≫1 \) , Eq. (6) can be replaced by an approximate form

\( T≈\frac{16{α^{2}}{k^{2}}{e^{-2αL}}}{{(α-ik)^{2}}}≈{e^{-2αL}}={e^{-\frac{2}{ℏ}[2m{({V_{0}}-E)^{1/2}}L]}},\ \ \ (7) \)

which is the transmission coefficient of single potential barrier.

2.2. Double Potential Barrier Model

Consider a particle moving from left to right with energy \( E \) , and the potential energy for two symmetrical barriers is \( {V_{0}} \) . Using the same ideal in Sec. 2.1, assuming the particle energy is less than the barriers energy ( \( E \lt {V_{0}} \) ), which is shown in Figure 2.

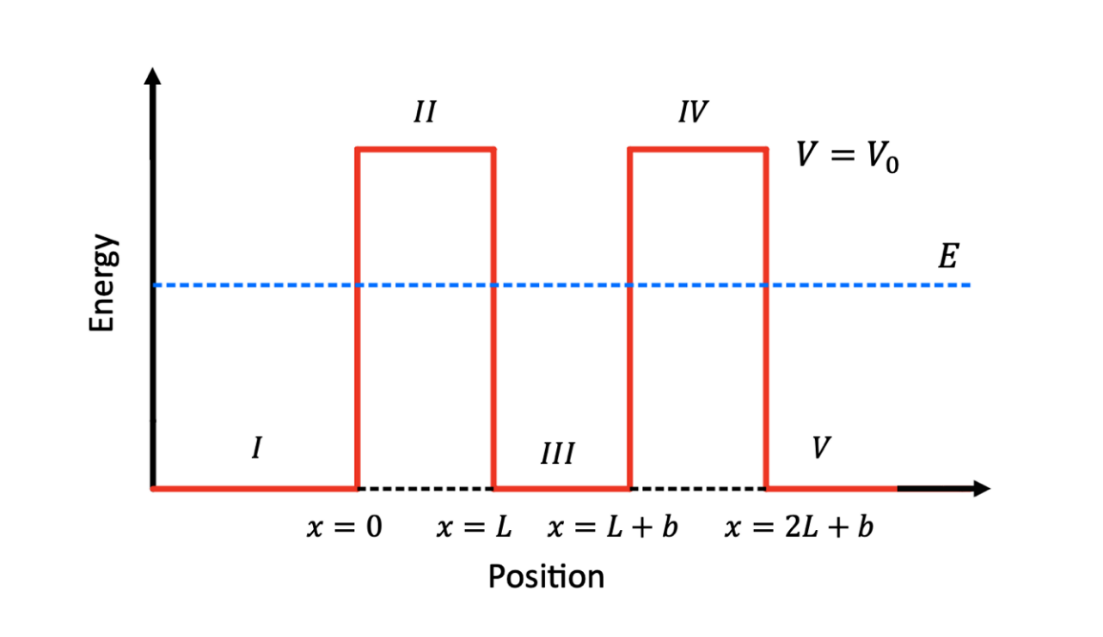
Figure 2. Double potential barrier model. \( E \) is the energy of particle energy, \( V \) is the potential energy of barriers, and \( x \) is the position.

The potential energy function is

\( V(x)=\begin{cases} \begin{array}{c} {V_{0}}, 0 \lt x \lt L, L+b \lt x \lt 2L+b \\ 0, x \lt 0, L \lt x \lt L+b, x \gt 2L+b \end{array} \end{cases}.\ \ \ (8) \)

In this model, there are five regions in total. For region I, II, III and IV, the wave function has both incident and reflected possibility by the barrier boundary. In region V, there will be only the transmitted wave function. The paper aims to find the general solutions in each region, which are

\( Region I: {ψ_{I}}(x)={A_{0}}{e^{+ikx}}+A{e^{-ikx}}\ \ \ (9) \)

\( Region II: {ψ_{II}}(x)=B{e^{-αx}}+C{e^{+αx}}\ \ \ (10) \)

\( Region III: {ψ_{III}}(x)=D{e^{+ikx}}+E{e^{-ikx}}\ \ \ (11) \)

\( Region IV: {ψ_{IV}}(x)=F{e^{-αx}}+G{e^{+αx}}\ \ \ (12) \)

and

\( Region V: {ψ_{V}}(x)=H{e^{ikx}}\ \ \ (13) \)

in which \( k=\frac{\sqrt[]{2mE}}{ℏ} \) , \( α=\frac{\sqrt[]{2m({V_{0}}-E)}}{ℏ} \) .

At the boundary of each potential, the wave function and its first-order derivative must be continuous. From the equality of the wave function as well as its first-order derivatives at the boundary, the authors obtain the following four pairs of equations:

\( x=0: \begin{cases} \begin{array}{c} {A_{0}}+A=B+C \\ ik{A_{0}}-ikA=-αB+αC \end{array} \end{cases}\ \ \ (14) \)

\( x=L: \begin{cases} \begin{array}{c} D{e^{ikL}}+E{e^{-ikL}}=B{e^{-αL}}+C{e^{+αL}} \\ ikD{e^{ikL}}-ikE{e^{-ikL}}=-αB{e^{-αL}}+αC{e^{+αL}} \end{array} \end{cases}\ \ \ (15) \)

\( x=L+b: \begin{cases} \begin{array}{c} F{e^{-α(L+b)}}+G{e^{+α(L+b)}}= D{e^{ik(L+b)}}+E{e^{-ik(L+b)}} \\ -αF{e^{-α(L+b)}}+αG{e^{+α(L+b)}}=ikD{e^{ik(L+b)}}-ikE{e^{-ik(L+b)}} \end{array} \end{cases}\ \ \ (16) \)

and

\( x=2L+b: \begin{cases} \begin{array}{c} {He^{ik(2L+b)}}=F{e^{-α(2L+b)}}+G{e^{+α(2L+b)}} \\ ikD{e^{ik(2L+b)}}=-αF{e^{-α(2L+b)}}+αG{e^{+α(2L+b)}} \end{array} \end{cases}\ \ \ (17) \)

Similarly, after solving the boundary conditions, one can find the ratio of the transmitted current to the incident current, which is expressed as

\( T=\frac{{({k^{2}}+{α^{2}})^{2}}{cosh^{2}}(αL)-2({k^{2}}+{α^{2}})({k^{2}}-{α^{2}})}{{({k^{2}}+{α^{2}})^{2}}{cosh^{2}}(αL)-2({k^{2}}+{α^{2}})({k^{2}}-{α^{2}})+(4{k^{2}}{α^{2}}{cosh^{2}}(αL)-4{k^{2}}{α^{2}}){sin^{2}}(kb)}\ \ \ (18) \)

The Eq. (18) is the transmission coefficient of the particles in double potential barrier.

3. Applications

In this section, the authors delve into the practical implications and real-world applications of the insights gained from our study on quantum tunnelling effect. As documented by Lovas at 1998, the transmission coefficient of \( α \) practical that is conducted by the continuity of wave equation and Schrodinger’s equation can be used to resolve the half-life of alpha practical

\( {T_{\frac{1}{2}}}=\frac{ln2}{nP},\ \ \ (19) \)

Here, \( n \) is the number of times the particle hit the wall of barrier in per unit time and \( P \) is transmission probability [7].

By the calculation conducted by Lui using Mathematica program, the relationship between the half-life and the kinetic energy is unveiled, and it is equivalent to the one found by Geiger and Nuttall in experiment. The relation is shown as follows, which also nicely shows the consistency of theoretical and experimental results

\( ln{T_{\frac{1}{2}}}=A{E^{-\frac{1}{2}}}+B\ \ \ (20) \)

where \( n \) this form A and B are constant related to nucleus of decay. This simple relationship can be applied to compute the half-life of material exhibit extremely brief or prolonged radioactive decay.

Moreover, quantum tunnelling has efficiently application in condensed matter physics. according to the study conducted by Wang, it has found that single-layer graphene has affluent tunnelling characteristics. In tow-dimensional square barrier situation graphene has shown it’ s superb electrical conductivity and the excellent property as semiconductor. Wang studied how is transmission coefficient vary as changes in angle of incidence in different height and width of barrier. When an electron with an incident angel \( φ \) is encountered, the wave functions of the external and internal wave vectors of the potential barrier are as follows:

\( {ψ_{1}}(x,y)=\begin{cases} \begin{array}{c} ({e^{i{k_{x}}x}}+r{e^{-i{k_{x}}x}}){e^{i{k_{y}}y}}, x \lt 0 \\ (a{e^{i{q_{x}}x}}+b{e^{-i{q_{x}}x}}){e^{i{k_{y}}y}}, 0 \lt x \lt d \\ t{e^{i{k_{x}}x+i{k_{y}}y}}, t \gt d \end{array} \end{cases}.\ \ \ (21) \)

and

\( {ψ_{2}}(x,y)=\begin{cases} \begin{array}{c} s({e^{i{k_{x}}x+iΦ}}-r{e^{-i{k_{x}}s-iΦ}}){e^{i{k_{x}}y}}, x \lt 0 \\ s \prime (a{e^{i{q_{x}}x+iθ}}-b{e^{-i{q_{x}}x-iθ}}){e^{i{k_{x}}y}}, 0 \lt x \lt d \\ st{e^{i{k_{x}}x+i{k_{y}}y+iθ}}, t \gt d \end{array} \end{cases}.\ \ \ (22) \)

Here, \( {k_{f}} \) is femi wave vactor, \( {k_{x}} \) and \( {k_{y}} \) is external wave vector component, \( {q_{x}} \) is the \( x \) -component of the wave vector inside the potential barrier, \( θ=arctan{(\frac{{k_{x}}}{{q_{x}}})} \) is relax angle, \( s=sgn(E) \) and \( s \prime =sgn(E-{V_{0}}) \) . Also, based on the continuity conditions at the boundary, the coefficients \( a \) , \( b \) , \( t \) , \( r \) , and transmission probability can be determined.

The result shows that the transmission probability is equally coincide to 1 as long as this incident angel \( φ \) is close to 0. Furthermore, this result is not influenced by the width and height of the potential barrier [8]. According to quantum scattering theory, the probability of tunnelling decays exponentially with the height and width of the potential barrier. When charge carriers in graphene approach speeds close to 1/300th of the speed of light, relativistic effects cannot be ignored. The Dirac equation has previously predicted that relativistic electrons can completely penetrate potential barriers [9], and carriers in graphene are considered massless fermions, thus following the Dirac equation. This type of tunnelling situation is also referred to as Klein tunnelling, which is a significant reason for the excellent electrical conductivity of graphene.

Nuclear quantum tunnelling significantly affects the recombination dynamics of polaronic electron-hole pairs within the crystalline lattice of hematite, a distinct form of iron oxide [10]. In the study conducted by Fan et al, it was observed that due to strong electron-phonon coupling, the charge carrier displaces the equilibrium position of ions, creating a potential well that entraps the carrier itself [11]. In α-Fe₂O₃, optical excitation generates free electrons and small polarons, which interact with lattice deformations, leading to the formation of a potential well that captures the charge carriers. Under low-temperature conditions, the influence of quantum tunnelling enables these small polarons to transition to lower energy states without the need to overcome significant energy barriers.

The exploration extends to the double potential barrier model, considering both symmetrical and unsymmetrical barriers. General solutions for the wave function are derived in each region, and boundary conditions yield a transmission coefficient for the particle passing through the barriers. The practical applications of quantum tunnelling are discussed, ranging from its role in determining the half-life of alpha particles to its significance in condensed matter physics, particularly in materials like single-layer graphene. The study of transmission coefficients in graphene reveals its exceptional electrical conductivity and semiconductor properties.

4. Conclusion

The exploration of quantum tunnelling in the context of single and double potential barriers reveals the profound impact of quantum mechanics on our understanding of particle behavior. The single potential barrier model provides a theoretical framework for elucidating the probabilities associated with particles traversing energy barriers, showcasing the departure from classical mechanics. The derived transmission coefficients unveil the counterintuitive nature of quantum tunnelling, allowing particles to penetrate barriers even when their energy is lower than the barrier height. The extension to the double potential barrier model further emphasizes the versatility and practical applications of quantum tunnelling. This phenomenon, where particles exhibit probabilities of passing through two successive barriers, finds relevance in semiconductor technology and nanotechnology. Quantum mechanics, in contrast to classical physics, enables the explanation of conduction in microscopic devices, expanding the horizons of technological applications. The findings presented in this study not only contribute to a deeper comprehension of quantum phenomena but also underscore the potential for leveraging these principles in cutting-edge technologies. The ability to control and utilize quantum tunnelling opens avenues for innovations in electronic devices and materials science. As the authors continue to delve into the intricacies of quantum mechanics, the insights gained from this study pave the way for future advancements in quantum computing, nanoelectronics, and beyond. In essence, the study of quantum tunnelling serves as a bridge between theoretical principles and practical applications, offering a glimpse into the transformative possibilities that quantum mechanics holds for the future of technology.

Authors Contribution

All the authors contributed equally and their names were listed in alphabetical order.