1. Introduction

Navier-Stokes equation (NSE) was derived based on Euler’s equation with viscosity effect by Claude Navier in 1822. The NSE was extended to a series of continuous derivations on a combination of parameters of stress and strain, incompressible and compressible flow by Poisson, De Saint-Venant and George Stokes. From Newton’s second law, the NSE describes the relations between velocity, density, pressure and temperature of flow motion with a general equation of continuity of mass, conservation of momentum and conservation of energy [1]. The general equation of NSE illustrates the relations of change of velocity, convection of flow, pressure change, and external body force such as gravity, electromagnetic, and viscosity effects. The flow diffusion and energy dissipation are crucial to the analysis of NSE in fluid dynamics [2].

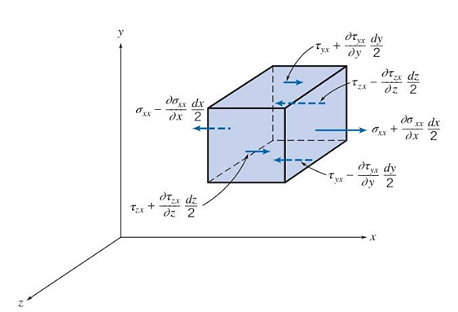
Figure 1. Element of NSE [3]

NSE:

\( ρ[\frac{∂u}{∂t}+(u∙∇)u]=-∇P+ρg+μ{∇^{2}}u\ \ \ (1)\ \ \ \ \ \ \)

Continuity of mass:

\( \frac{∂p}{∂t}+\frac{∂(ρu)}{∂x}+\frac{∂(ρw)}{∂z}=0 \ \ \ (2) \)

Conservation of momentum:

\( \frac{∂(ρu)}{∂t}+\frac{∂(ρu2)}{∂x}+\frac{∂(ρuv)}{∂y}+\frac{∂(ρuw)}{∂z}=-\frac{∂ρ}{∂x}+\frac{1}{Re}[\frac{∂{τ_{xx}}}{∂x}+\frac{∂{τ_{xy}}}{∂y}+\frac{∂{τ_{xz}}}{∂z}] \)

\( \frac{∂(ρv)}{∂t}+\frac{∂(ρuv)}{∂x}+\frac{∂(ρv2)}{∂y}+\frac{∂(ρuw)}{∂z}=-\frac{∂ρ}{∂y}+\frac{1}{Re}[\frac{∂τxy}{∂x}+\frac{∂{τ_{yy}}}{∂y}+\frac{∂{τ_{yz}}}{∂z}] \)

\( \frac{∂(ρw)}{∂t}+\frac{∂(ρuw)}{∂x}+\frac{∂(ρuw)}{∂y}+\frac{∂({ρw^{2}})}{∂z}=-\frac{∂ρ}{∂z}+\frac{1}{Re}[\frac{∂{τ_{xz}}}{∂x}+\frac{∂{τ_{yz}}}{∂y}+\frac{∂{τ_{zz}}}{∂z}]\ \ \ (3) \)

Conservation of energy:

\( \frac{∂(E)}{∂t}+\frac{∂(uE)}{∂x}+\frac{∂(vE)}{∂y}+\frac{∂(wE)}{∂z}= \\ -\frac{∂(up)}{∂x}-\frac{∂(vp)}{∂y}-\frac{∂(wp)}{∂z}-\frac{1}{RePr}[\frac{∂qx}{∂x}+\frac{∂qy}{∂y}+\frac{∂qz}{∂z}] \\ +\frac{1}{Re}[\frac{∂}{∂x}(u{τ_{xx}}+v{τ_{xy}}+w{τ_{xz}})+\frac{∂}{∂y}(u{τ_{xy}}+v{τ_{yy}}+w{τ_{yz}})+\frac{∂}{∂z}(u{τ_{xz}}+v{τ_{yz}}+w{τ_{zz}})]\ \ \ (4) \)

In three dimensions, the NSE has a formula of continuity, conservation of momentum and energy concerning the coordinates of (x,y,z) , velocity u(u,v,w), Renold number Re, pressure P, density ρ, energy E, heat flux q, the strain σ and stress \( τ \) of element in Figure 1, and Prandtl number Pr of viscosity [2].

This paper analyzes the perspectives of previous research on solutions of NSE and their relative applications. limitations such as boundary and initial conditions are applied to the demonstration of the hypothesis and theories of the solution of the 3D NSE from previous research. The solutions of NSE imply the energy dissipate and vorticity properties. Meanwhile this paper focuses on the study of solutions and turbulence models of NSE contributed to the applications on aerodynamics. Machine Learning and Neural Networks are applied to the solution of the NSE to improve the accuracy of prediction of fluid motion. Aerodynamics applications on airfoil, turbulence model, design of propeller and ejection seats are discussed with analysis of solutions of NSE.

Because of the wild use of NSE in fluid dynamics, turbulence study and applications of aerodynamics, solutions of NSE concerning the incompressible/compressible flow with models of boundary and initial conditions are developed in mathematical and numerical methods. The motivation of this paper is focusing on the brief study of solutions of NSE and models, the applications of NSE on aerodynamics are also discussed. With the contribution of Machine learning, accurate and global solutions are expected to be computed for the NSE in the future.

2. Solutions of NSE

Because of the influence of the viscosity of the fluid, the solutions of NSE depend on the structure of the fluid. The NSEs have unique solutions only for the laminar flow, low Renold number given by the Dirac-like initial condition U(x,0) and physical Stokes hypothesis of linear fluids [4]. The nonlinear differential operator, such as Korteweg-de Vries (KdV) equation type, constitutes the momentum and kinetic energy flow. At high Renold numbers, the hybrid models of Renold averaged Navier-Stokes equation (RANS) are applied to turbulent kinetic energy and shear stress prediction [5]. The viscous fluid with sufficiently small viscosity is due to the boundary layer [6]. The limitation of thin layer of fluid near boundary leads to the instability and turbulence structure compared with Euler’s equation [5].

Figure 2. Plot of magnitude of vorticity of NSE at Re = 874 [7]

Three-dimensional incompressible NSE:

\( {u_{t}}-∆u+ (u ∙ ∇)u+ ∇p= 0 \)

\( div u= 0\ \ \ (5) \)

Strong solutions of NSE have local time and global in time existence and uniqueness in small initial data at equilibrium. The cauchy problem of NSE considers the heat conductivity as boundary condition [8]. The Cauchy problem transforms the NSE system to local existence and uniqueness of solutions with bounded domain and initial data [9]. When the initial data is large or with arbitrary energy, the weak solution is used to analyse the energy balance and dissipation with Navier boundary condition which allows for no-slip and slips for compressible and incompressible flow [10].

Leray–Hopf weak solutions for the forced NSE can be expressed in time-averaged form with Sobolev norms [11]. The energy inequality estimates the smooth bounded domain and boundary layer to model the energy dissipation of fluid with small viscosity [12]. The Leray solutions that satisfy the energy inequality in the boundary domain can also be applied to the multifractal set with energy dissipation combined with the multifractal theory of Parisi and Frisch [13].

\( {∂_{t}}{u^{ν}} + {u^{ν}} · ∇{u^{ν}} + ∇{P^{ν}} = ν∆{u^{ν}} + {f^{ν}} div {u^{ν}} = 0 in Ω \\ \ \ \ (6) \)

Fujita-Kato theory of mild solution for equation (6) provides semigroup proof of the NSE with norm of initial data in \( {L^{3}} \) , heat energy and regularization of the initial data [14]. The unique global solution is derived from the small differentiation operator [15].

\( {‖{u_{0}}‖_{{\dot{H}^{\frac{1}{2}}}}}≝{({|{\hat{u}_{0}}(ξ)|^{2}}dξ)^{\frac{1}{2}}} \ \ \ (7) \)

A study on the axially symmetric NSE provides smooth solutions on the small initial data of global regularity conditions. The energy identity and vorticity can be computed following the maximum principle of L∞ norm [16]. By study the vorticity around symmetry axis form burgers vortex exact solution of NSE, the stretched vorticity filed with nonzero radial and azimuthal components can sustain vortex sheet type of solutions around axial direction [17].

Machine learning model is developed to improve the efficient and accuracy of RANS solutions with complex flow regimes, boundary layers and conditions. With the neural network and Direct Numerical Simulation (DNS), the enhanced Lager Eddy Simulation (LES) model of RANS performed accurate prediction of turbulent kinetic energy and shear stress [18].

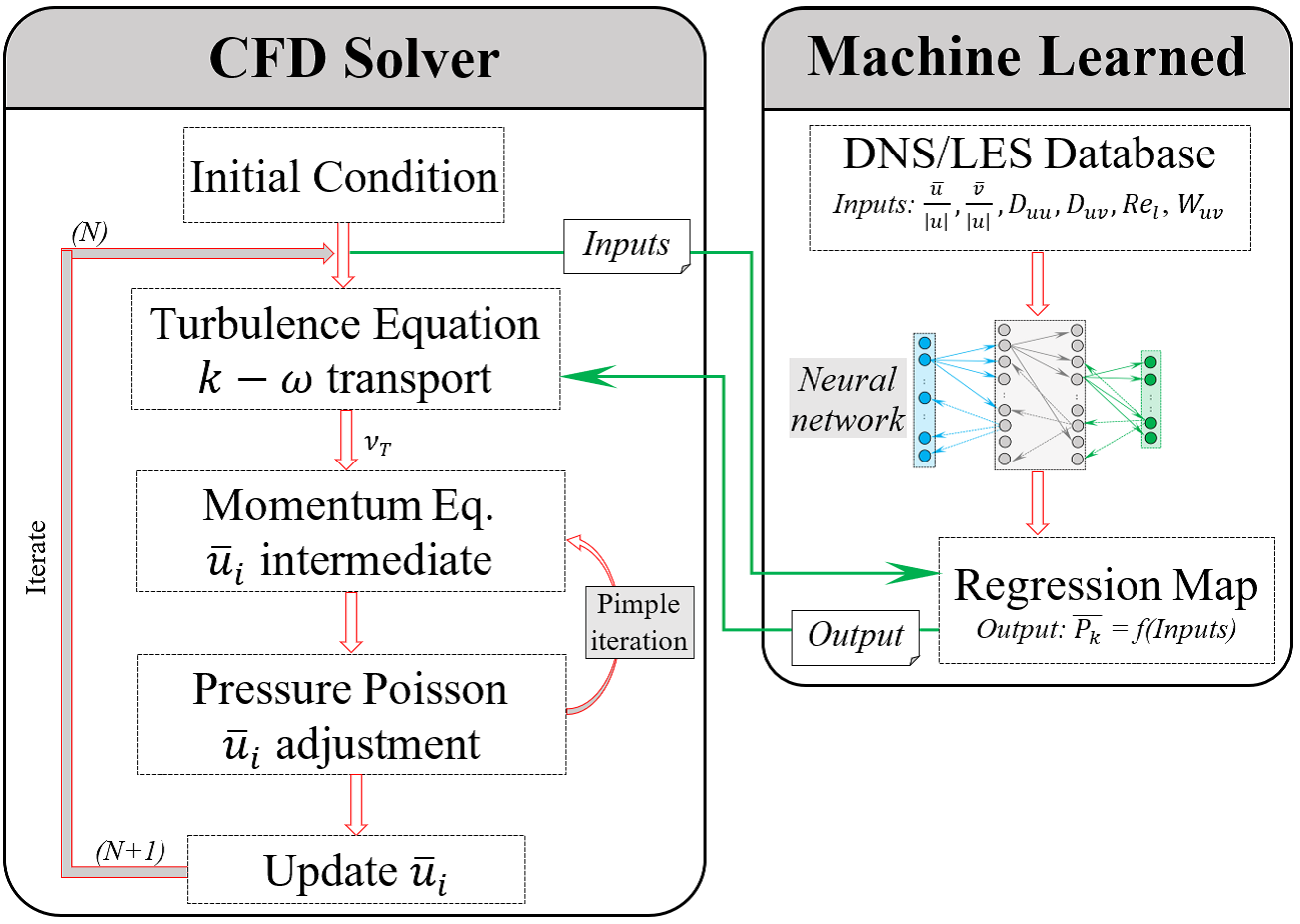
Figure 3. Schematic diagram of RANS solutions process and coupling with machine learned turbulence model [6]

The Physics-informed Neural Networks combines the turbulence model of eddy viscosity and fractional derivative based diffusion models of RANS [19]. The Neutral Networks led fractional RANS solution analyzes the motion form DNS with complex boundary conditions of turbulent Couette, channel, and pipe flow. In the research of hyper reduced-order modeling [20], The Neural Networks quantify the incompressible NSE solutions on the discrete finite dimensions. On the spaces explicated by finite volume method, finite element method, and spatial element methods, the Neural Networks trains the snapshots to update the NSE solutions.

Quantum computing and algorithms are developed rapidly to simulate the fluid dynamics. The NSE solutions update to hydro-dynamics Schrodinger equation such as incompressible Schrodinger flow (ISF), with local quantum-gravity ponderomotive force [21]. When DNS transfer measurement to simulation and quantities, the vorticities in turbulence can be plot in magnitudes.

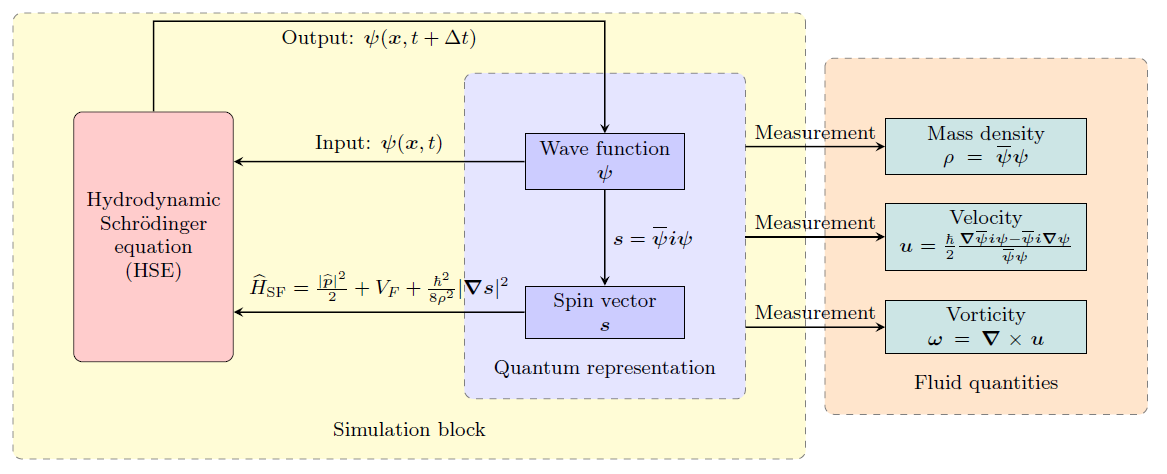
Figure 4. strategy of quantum computing [10]

Figure 5. Isosurface of vortices in the ISF [10]

3. Applications on Aerodynamics

Because of the crucial illustration of fluid motion, the NS equations are applied to the aerodynamics analysis. In the simulation and test of the NACA airfoil with changing Mach number [9], the NS equations are developed to combine with the neural network to present linear projection-based reduction-order model. NACA airfoil test case with computational domain in compressible NS equation system was operated to represent the manifold of velocity field corresponding to the Mach number.

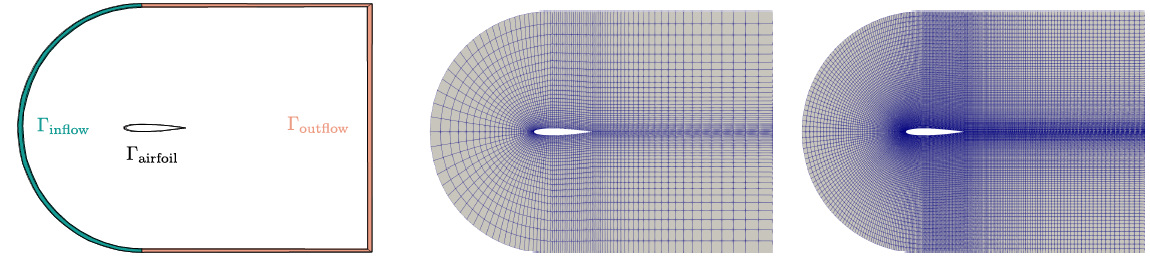
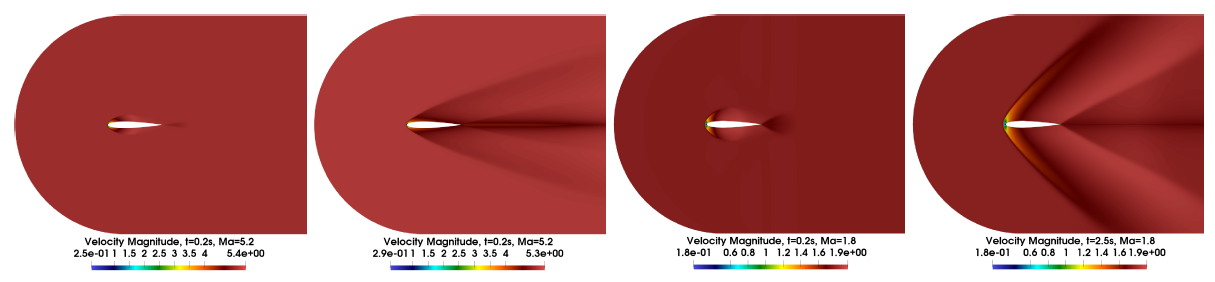
Figure 6. Computational domain and snapshots of the velocity field of NACA airfoil [9]

The model of Ahmed’s body with an eddy model of turbulence was simulated and tested based on the extended NS equations [9]. The study trained the NS system with reduced-order Modelling concerning changing of slant angle. the NSE system presented the manifold of velocity and pressure of Ahmed body from predicted simulation and test.

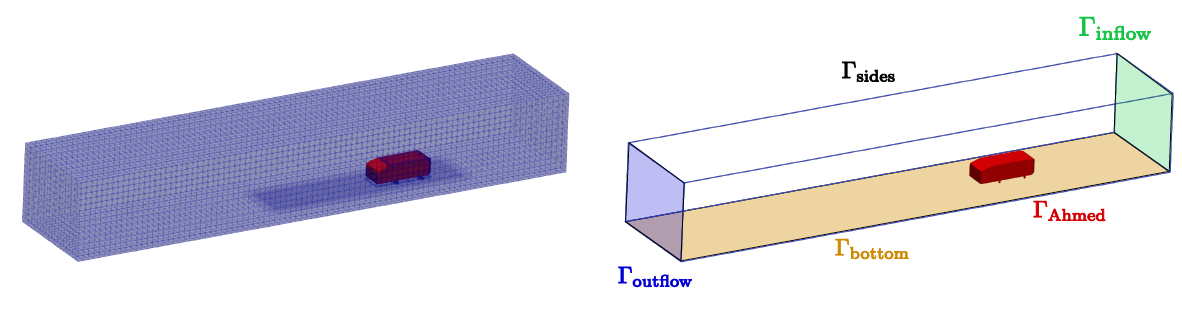
Figure 7. Ahmed body simulation and test [9]

The nonlinearities of NSE give coupled set of equations of coarse-graining approach with interpretation and rigorous analysis, hence, the basis of large-eddy simulation (LES) [18]. The energy dissipation transfer can be analyzed with a scale-decomposition of the velocity into band-passed contribution. The eddy-viscosity model and hypothesis derive the solution of the closure problem for RANS equations [18]. The model of eddy-viscosity forms the strain-stress relationship in turbulence.

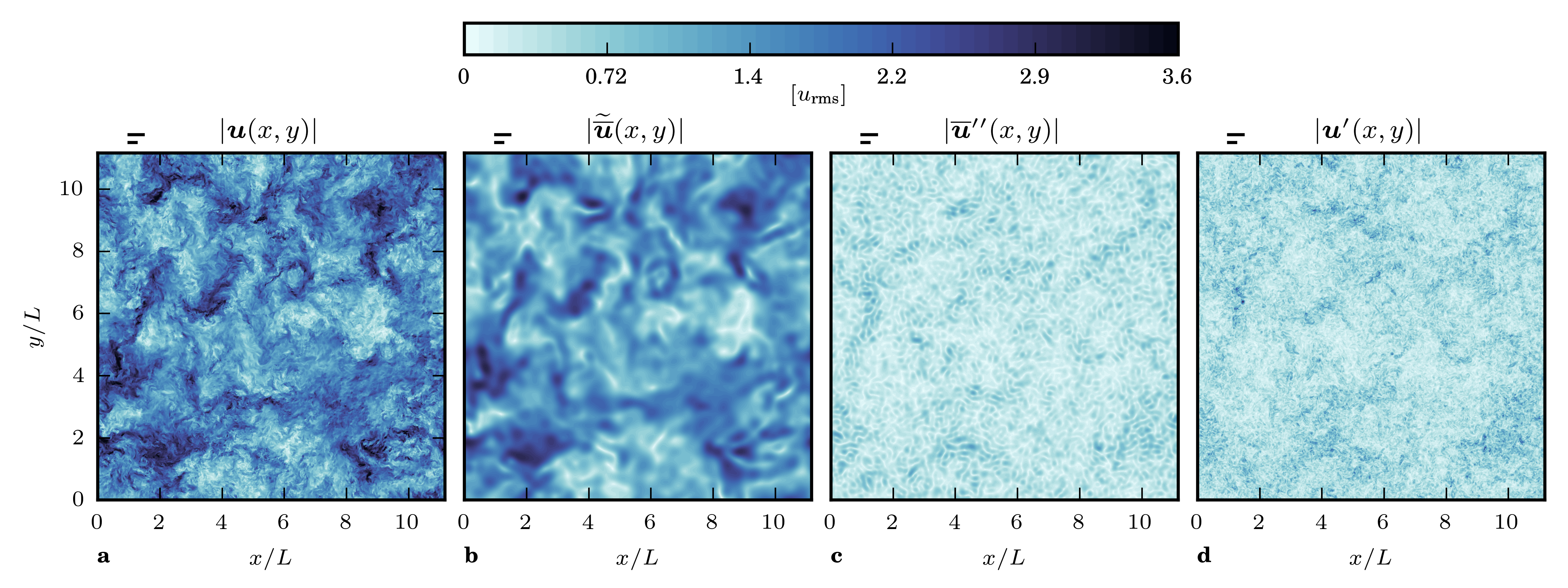
Figure 8. Visualizations of the amplitude of velocity of different scales in turbulence [8]

Aerodynamic Simulation on ejection seat can be performed with NSE with extended parameters such as aerodynamic force coefficient and aerodynamics moment coefficient. NSE system in 3D coordinate represents the continuity, conservation of momentum and energy of the ejection seat corresponding to changing angles and Mach numbers.

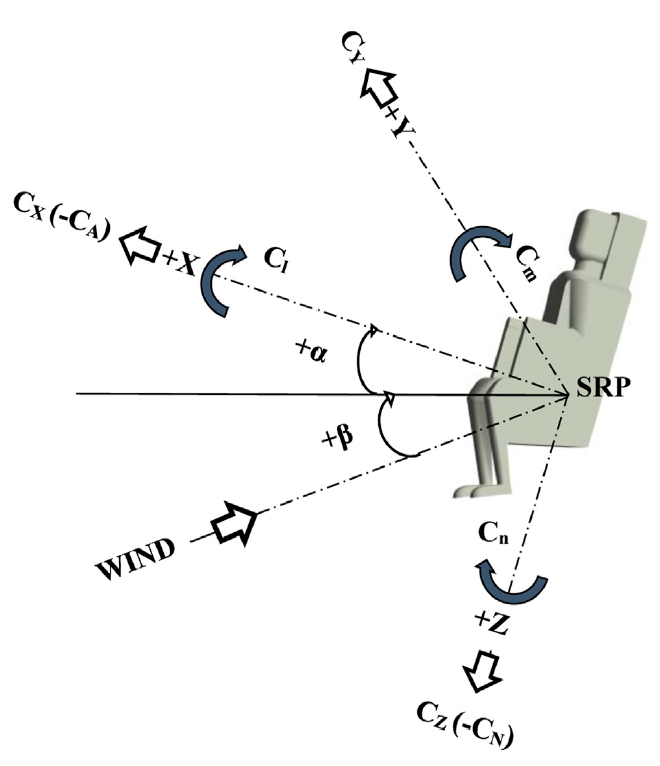
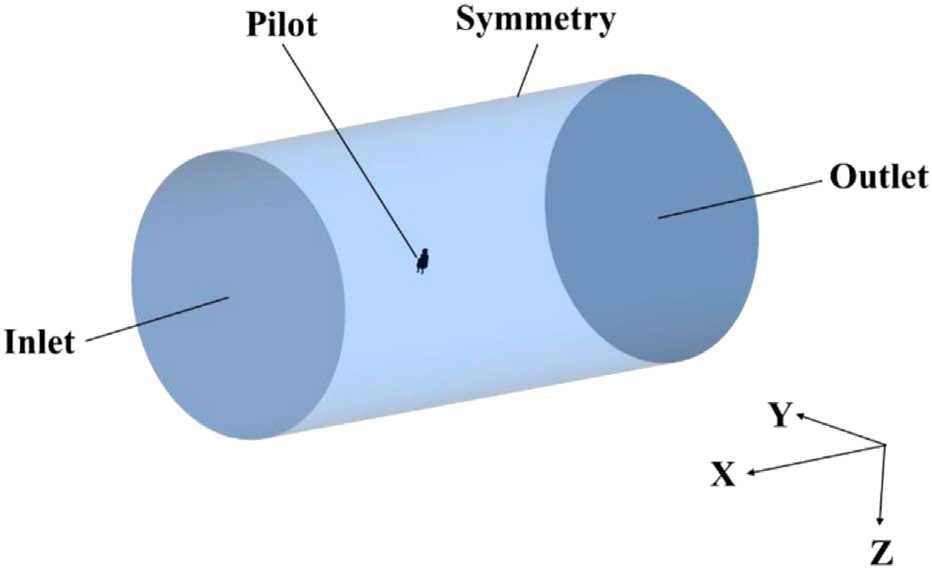
Figure 9. Simulation model of seat [14]

Figure 10. Vorticity contour of the model at α = −15° and Ma = 0.75. [14]

The RANS equation can be applied to the analysis of the turbulent nature of flow with the k-ω SST model and Gamma Re Theta laminar-turbulent transition model. In real engineering applications, the RANS equations are used to describe the turbulent motion of viscous liquid/gas around the propeller flow [21]. The numerical simulation results obtained correspond to the velocity manifold representing the distribution of cavitation. Hence, the RANS system developed the design of the propeller.

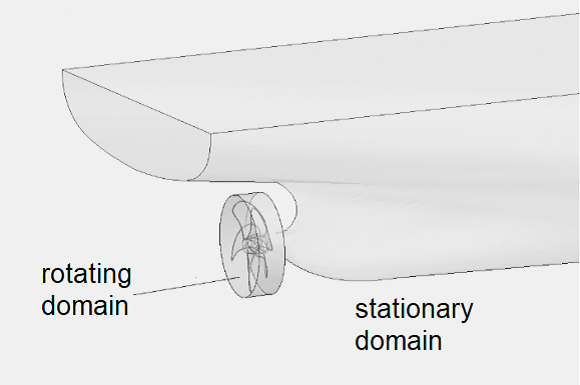
Figure 11. Propeller domain and velocity manifold [15]

4. Conclusion

This paper studies the 3D NSE and solutions corresponding to the Cauchy problem with initial data, boundary conditions of Larey’s solution and advanced mild solutions from research of Fujita & Kota. The axial asymmetry model of NSE and stretched vorticity fields can be analyzed by computing the smooth solutions of NSE with regularity conditions. The ML and Neural Networks are applied to iterate the process of predictive regulation of the NSE system. Applications on aerodynamics are discussed on the NACA airfoil simulation and test, eddy-model of turbulence analysis and design of propeller and ejection seats. This paper can have improvement on the collection of computational and experimental data and research on turbulence models. the computational simulations and experiments contribute to the study of fluid dynamics of NSE since the properties of vorticity discussed in this paper performed a crucial role in the analysis of hypotheses and theories of solutions of NSE. Machine learning provides an efficient method to compute and simulate the NSE concerning the type of turbulent model, hence, the trend of exploration of solutions of NSE concentrates on the complicated combination of NSE with a quantic nature such as ISF discussed in this paper. The properties of energy and vorticity are also the consideration of applications of NSE in fluid dynamics. With the development of Machine learning and Neural Networks, the analysis of models of exact and hybrid solutions such as RANS can perform accurate simulations and regularity of conditions of existence and uniqueness of solutions of NSE.