1 Introduction

A simple pendulum, a typical model of simple harmonic motion (SHM) in which an object oscillates with no energy loss and constant maximum displacement[1] is defined as a system in which a small object with uniform mass is suspended from the end of a light string[2]. My interest in investigating the relationship between the period of a pendulum and the number of strings originated from my notice when studying simple harmonic motion that mass of the string is assumed to be negligible in the derivation of the period of a simple pendulum. I was then curious about what the expression would be if it was non-negligible. In order to make it more significant compared with mass of the bob, I decided to gradually increase the number of strings, which could also assist me in collecting more data and therefore obtaining a general relationship between the period of the pendulum and mass of the string.

In the simplest situation, the expression for the period of a simple pendulum is known as:

\( T=2π\sqrt[]{\frac{L}{g}} \)

where \( L \) is the length of the pendulum and \( g \) is the acceleration due to gravity.

For a simple pendulum, the whole system is treated as a point mass as the mass of the string is ignored. However, in a general situation, an object whose motion represents that of a simple pendulum usually cannot be regarded as a point mass. The mass distribution should be therefore taken into account[3]. Even though the analysis is more complicated, the expression for its period should have the same form of \( T=2π\sqrt[]{⋯} \) as the derivation is similar.

2 Theory

To simplify the whole analysis, I assume each string has equal mass as it is hard to ensure they all have equal lengths. Also given that the wire is not perfectly uniform, this assumption becomes more necessary. I also ignore the radius of the bob as it could be regarded to be insignificant compared with the length of strings.

Figure 1. A simple pendulum, accessed at Britannica.com.[4]

The moment of inertia of the bob and strings about the pivot is respectively:

\( I_{bob}=ml^{2} \)

\( I_{string}=\frac{1}{3}nMl^{2} \)

The moment of inertia of the system about the pivot is therefore:

\( I=I_{string}+I_{bob}=\frac{1}{3}nMl^{2}+ml^{2}=(\frac{1}{3}nM+m)l^{2} \)

where l is the length of strings, m represents mass of the bob, M represents mass of each string and n is the number of strings.

The distance from the center of mass (CM) of the system to the pivot is:

\( r_{CM}=\frac{\sum_{}^{} mr}{\sum_{}^{} m}=\frac{nM∙\frac{l}{2}+ml}{nM+m}=\frac{\frac{1}{2}nM+m}{nM+m}l \)

By definition of torque and according to Newton’s second law in rotational motion,

\( \vec{τ}=\vec{r}×\vec{F}=Iα \)

therefore:

\( τ=-(\frac{l}{2}∙nMg+mgl)sin{θ}=Iα \)

where \( α \) is the angular acceleration of the system.

\( -(\frac{1}{2}nM+m)glsin{θ}=Iα \)

According to Maclaurin’s series[5],

\( sin{θ}=θ-\frac{θ^{3}}{3!}+\frac{θ^{5}}{5!}-\frac{θ^{7}}{7!}+⋯+\frac{(-1)^{n}θ^{2n+1}}{(2n+1)!}+⋯ \)

When \( θ \) is small, terms \( \frac{θ^{3}}{3!}, \frac{θ^{5}}{5!}, \frac{θ^{7}}{7!}, ⋯, \frac{(-1)^{n}θ^{2n+1}}{(2n+1)!} \) could all be ignored. Therefore, \( sin{θ}≈θ \) for small values of \( θ \) .

Returning to the equation above,

\( τ=-(\frac{1}{2}nM+m)glθ=(\frac{1}{3}nM+m)l^{2}α \)

\( -(\frac{1}{2}nM+m)gθ=(\frac{1}{3}nM+m)lα \)

\( α=-\frac{g(\frac{1}{2}nM+m)}{l(\frac{1}{3}nM+m)}θ \)

Since the position function for a particle in simple harmonic motion is:

\( x(t)=Acos{(ωt+φ_{0})} \)

where \( x \) is displacement, \( A \) is the amplitude of the motion, \( ω \) is angular frequency, and \( φ_{0} \) is the initial phase of the motion.

\( v(t)=\frac{dx}{dt}=-Aωsin{(ωt+φ_{0})} \)

\( a(t)=\frac{dv}{dt}=-Aω^{2}cos{(ωt+φ_{0})} \)

It could be clearly seen that \( a=-ω^{2}x \) . In this situation, the system is in rotational motion, therefore \( a \) is replaced by \( α \) , the angular acceleration, and \( x \) is replaced by \( θ \) , the angular displacement. Then the equation becomes \( α=-ω^{2}θ \) .

Returning to the analysis above,

\( α=-\frac{g(\frac{1}{2}nM+m)}{l(\frac{1}{3}nM+m)}θ \)

therefore, the angular velocity is expressed as:

\( ω=\sqrt[]{\frac{g(\frac{1}{2}nM+m)}{l(\frac{1}{3}nM+m)}} \)

\( T=\frac{2π}{ω}=2π\sqrt[]{\frac{l(\frac{1}{3}nM+m)}{g(\frac{1}{2}nM+m)}} \)

where \( T \) is the period of the pendulum.

The relationship between the period of the system and the number of strings is rearranged as follows.

\( T^{2}=4π^{2}\frac{l}{g}(\frac{\frac{1}{3}nM+m}{\frac{1}{2}nM+m})=4π^{2}\frac{l}{g}(1-\frac{nM}{3nM+6m}) \)

3 Hypothesis

As the number of strings \( n \) is my independent variable and the period of the pendulum \( T \) is the dependent variable, I decided to plot \( T^{2} \) against \( 1-\frac{nM}{3nM+6m} \) and I suppose it to be a straight line according to the relationship deduced above.

4 Method

For the set-up of the experiment, I first tried a protractor-nail combination. The protractor could be used to measure the released angle and thus ensure that it is constant and small while the string can be held on the nail. However, the nail was rusty and extremely dangerous. Also considering that it was hard to accurately measure the angle as the pendulum was not perfectly aligned with the \( 90° \) scale on the protractor due to the clip, I finally gave up this apparatus. Instead, I used a stand, a clamp and a G-clamp. The G-clamp is used to fix the stand on the table. A clip was also applied to fix the string-bob system on the clamp. The main drawback of this set-up is that the released angle cannot be measured.

The pendulum bob is a glass ball with a piece of tape so that strings can be tied to it. As for the string, I used thick copper wire whose mass is significant compared to the pendulum bob.

Figure 2. Set-up of the experiment

I changed the number of strings each time and kept the length of strings, mass of the bob and the released angle constant. The strings were about \( 1m \) and the same bob was used throughout the experiment. To make sure the released angle was not changed, I placed a ruler close to the stand on the table, held the system near the ruler, made it aligned with the same scale on the ruler each time, and released it. The released angle was roughly \( 10° \) by estimate. As I observed that the strings would collide with the ruler every time they swung back, I removed the ruler after releasing the system and replaced it after collecting a value of the period.

I first conducted the experiment with only one piece of copper wire and gradually increased the number of pieces to change the number of strings. To achieve this, tape was applied to stick pieces of wire together. Since one period is too short to be accurately measured, I used a stopwatch to measure five periods of the system and repeated the steps three times for each number of strings to calculate average values of periods for simpler measurement and to reduce error.

5 Results

Raw data I obtained is shown in the table below.

Table 1. Raw data of mass

Table 2. Raw data of periods

Total mass of strings, or in other words, mass of six strings, is calculated using total mass minus mass of the bob.

\( m_{six strings}=43.27-21.38=21.89g \)

Mass of each piece of wire is then:

\( m=\frac{21.89}{6}≈3.65g \)

I used a stopwatch to measure my reaction time by counting 2.00s five times.

Table 3. Countings of 2.00s on a stopwatch

\( ∆t=\frac{t_{max}-t_{min}}{2}=\frac{2.09-1.94}{2}=0.075s≈0.08s \)

which is also the absolute uncertainty for 5 periods.

Average values of 5 periods for each number of strings are calculated.

Table 4. Average values of 5 periods

Since the reaction time is relatively constant, absolute uncertainty for each period is calculated by dividing the reaction time by 5, which is:

\( ∆T=\frac{0.075}{5}=0.015s≈0.02s \)

Table 5. Values of 1 period

Since when \( T=1.88s \) , percentage uncertainty in \( T^{2} \) is \( 2×(\frac{0.02}{1.88}×100%)≈2% \) and when \( T=1.78s \) , percentage uncertainty in \( T^{2} \) is \( 2×(\frac{0.02}{1.78}×100%)≈2% \) , percentage uncertainty for all values of \( T^{2} \) is about \( 2% \) .

Values needed to plot the graph along with the uncertainty are included in the table below.

Table 6. Processed data

A graph is drawn based on the processed data.

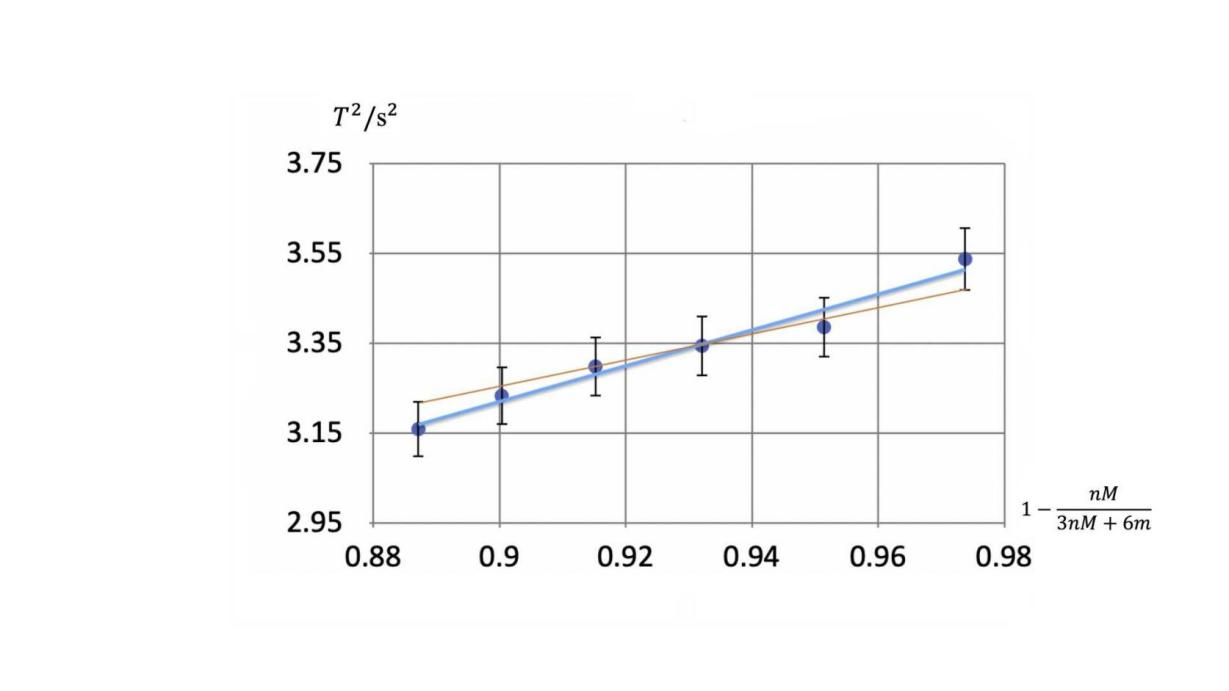
Figure 3. \( T^{2} \) against \( 1-\frac{nM}{3nM+6m} \)

The line of best fit in blue is generated by Numbers and its equation is \( y=3.98x-0.36 \) . The worst acceptable line with the potential minimum gradient in orange is drawn by connecting error bars and it is \( y=2.82x+0.72 \) .

The relationship between \( T^{2} \) and \( 1-\frac{nM}{3nM+6m} \) is therefore given by:

\( y=(4±1)x-(0±1) \)

It is rewritten as:

\( T^{2}=(4±1)(1-\frac{nM}{3nM+6m})-(0±1) \)

In theory, the gradient of the function is \( 4π^{2}\frac{l}{g} \) . In such a way, \( g \) , the gravitational field strength, could be calculated.

\( g=\frac{4π^{2}l}{gradient}=\frac{4π^{2}×1}{4}=9.87m/s^{2} \)

The real value of \( g \) is approximately \( 9.81m/s^{2} \) . Percentage error is:

\( \frac{9.87-9.81}{9.81}×100%=0.61% \)

When \( n=0 \) , which means that there is no string, or in other words, mass of the string is negligible, \( 1-\frac{nM}{3nM+6m}=1 \) , \( T^{2}=4s^{2} \) .

As derived above, \( T^{2}=4π^{2}\frac{l}{g}(\frac{\frac{1}{3}nM+m}{\frac{1}{2}nM+m})=4π^{2}\frac{l}{g}(1-\frac{nM}{3nM+6m}) \) .

Substitute \( n=0 \) into this equation,

\( T^{2}=4π^{2}\frac{l}{g}=\frac{4π^{2}×1.0}{9.81}=4.02s^{2} \)

which is included in the range of \( T^{2} \) when \( n=0 \) according to the expression obtained through my experiment.

6 Evaluation

In the graph of \( T^{2} \) against \( 1-\frac{nM}{3nM+6m} \) , the line of best fit passes through all error bars and the \( R^{2} \) value, a coefficient that “measures how well a statistical model predicts a result”[6], is 0.97, which is fairly close to 1. These results indicate that the experimental result is rather precise. As the values of periods are gained by measuring 5 periods, error is divided by five and is therefore reduced. Also considering that I repeated the experiment with each number of strings three times and calculated average values, data I obtained should be relatively accurate.

However, weaknesses still exist in the experiment. I applied tape to tie strings together, but its mass was not taken into account even though it seemed insignificant compared with total mass of the system. Due to imperfect measurement, the length of strings was not exactly \( 1m \) and there are slight differences between lengths of each string. Based on this, the approach of dividing the mass of six strings to calculate mass of each string is not accurate. Besides, as the number of strings increased, strings became harder to be straightened. This definitely has some impact on my final results.

Figure 4. Strings are not straight.

The percentage uncertainty was calculated by dividing the average reaction time by the average values of period and was approximated to be \( 2% \) for all numbers of strings. In fact, the real percentage uncertainties were between \( 2% \) and \( 2.5% \) exclusively and were different in values to 2 decimal places. The real error bars should be larger in such a case, causing greater ranges of results.

As the experiment progresses, I felt that I became more proficient in using the stopwatch, which means that the reaction time and absolute uncertainties for greater numbers of strings should be lower than predicted. The method of using the same percentage uncertainty for all values of period is therefore not so accurate.

Furthermore, as I held the system besides the stand and released it without measuring the released angle, the result is not accurate enough even though the angle is small by estimate. The ruler method to keep the released angle constant is also imprecise due to slight changes in the position of the ruler each time after it is replaced.

This experiment could be further improved by ensuring each string has approximately equal length and mass before measuring periods for each number of strings, but it is difficult to straighten the wire as it is firm, which means that the phenomenon of curved strings is inevitable. To address the problem of stopwatch usage, I could practice recording time several times before the experiment so that the reaction time would be more consistent. As for the problem of the tape, pieces of wire could be twisted together instead of being stuck so that the usage of tape could be avoided. However, it may complicate steps of the experiment and slightly reduce the length of the system, which may cause further errors in the length of strings. Meanwhile, if they are not evenly twisted together, the position of the center of mass may be changed, thereby generating more inaccuracies.

In addition, I did not take the uncertainty in lengths and masses into consideration as I supposed they are insignificant compared with the reaction time, which is the greatest source of error. However, for better and more precise results, they should not be ignored. To draw a more general conclusion, I could repeat the whole experiment with strings with other values of length or strings made of other material instead of copper.

7 Conclusion

Since data I collected is fairly close to the theoretical relationship between \( T^{2} \) and \( 1-\frac{nM}{3nM+6m} \) , a conclusion could be drawn that the period of a simple pendulum to the power of two is proportional to \( 1-\frac{nM}{3nM+6m} \) . The relationship is expressed as:

\( T^{2}=(4±1)(1-\frac{nM}{3nM+6m})-(0±1) \)

8 General result

For a pendulum system oscillating within small values of angle, and in the situation above, the bob and strings, the expression for the period could be derived using a similar approach.

\( τ=Iα=-mgrsin{θ} \)

where \( r \) is the distance from the center of mass to the pivot and \( m \) is mass of the system (different from \( m \) in the previous situation, which is the mass of the pendulum bob).

\( α=-\frac{mgrsin{θ}}{I} \)

As previously derived, \( sin{θ}≈θ \) for small values of \( θ \) and \( α=-ω^{2}θ \) ,

Therefore,

\( α=-\frac{mgrsin{θ}}{I}=-\frac{mgrθ}{I}=-ω^{2}θ \)

\( ω=\sqrt[]{\frac{mgr}{I}} \)

\( T=\frac{2π}{ω}=2π\sqrt[]{\frac{I}{mgr}} \)

This equation could be verified by substituting \( I=(\frac{1}{3}nM+m)l^{2} \) , \( m=nM+m \) and \( r=\frac{\frac{1}{2}nM+m}{nM+m}l \) . The same expression for the period in the previous situation will be obtained.

This expression for the period is not limited to a simple pendulum in which the oscillating object is approximated as a point mass. Instead, it can be applied in all situations in which an object oscillates about a fixed axis, especially when it cannot be considered as a point mass.

9 Application

The reason why the number of strings changes the period of the pendulum is that additional mass of each additional string changes both the total mass and the position of the center of mass of the system. According to the general result above, changes in those two quantities cause a change in the value of the period.

This principle could be applied in various situations. For instance, Big Ben, or Elizabeth Tower built in 1859 in London, England, is the most accurate chiming clock in the world[7]. To adjust its period, pre-decimal pennies are added onto the pendulum bob. Each penny increases the period of Big Ben by \( 0.4s \) per day[8]. Extra weight in the bob lowers the center of mass of the whole pendulum system and the period is therefore changed.

Table 7. Figures of the pendulum system

Figure 5. Double legged gravity escapement[12].

However, even though figures of mass of the penny and mass of components of the pendulum could be accessed, the change in period cannot be calculated by applying the equation derived above. The reason is that the pendulum system of Big Ben does not freely move under gravity. In fact, the motion of a pendulum in reality is not perpetual due to air resistance and friction among components. Instead, a double legged gravity escapement is used inside Big Ben to convert the energy of falling weight into impulses that retain the motion of the pendulum[11] and to prevent the pendulum from being susceptible to external factors like wind and thereby improving accuracy. Every time the pendulum swings to its highest position, it is pushed by one of the gravity arms. In other words, there is a reaction on it by the gravity arm. In such a case, the situation above cannot be applied.