1. Introduction

The Weil conjectures, proposed by André Weil in 1949, revolutionized algebraic geometry by linking the arithmetic properties of varieties over finite fields with topological concepts through cohomology theories. For a smooth projective variety X over a finite field Fq , Weil conjectured that the zeta function of X , which encodes information about the number of rational points on X over finite extensions of Fq , is a rational function. The conjectures further predict functional properties of this zeta function, analogous to the classical Riemann Hypothesis, and inspired the development of cohomology theories in characteristic zero. These cohomology theories, referred to collectively as “Weil cohomology,” adhere to certain axioms that allow the application of the Lefschetz trace formula, which expresses the count of fixed points of an endomorphism as an alternating sum of traces of the induced maps on cohomology groups. This formulation was pivotal, as it enabled Pierre Deligne’s eventual proof of the Riemann Hypothesis for varieties over finite fields. This thesis provides nothing new but an detailed introduction to the concepts underlying the Weil conjectures and the proof of Lefschetz trace formula, with some refinements in technical proofs.

2. Weil conjectures

In this paper, we shall now primarily consider X as a smooth projective variety, unless stated otherwise. While some definitions or results could be generalized to schemes, we omit these generalizations for simplicity.Also, from now on, we fix an algebraic closure Fq; thus, there exists a unique finite extension with degree r of Fq contained in Fq, namely Fqr.

To begin, we define rational points of the algebraic variety over a perfect field. We follow the definition given by Silverman in his [1, Chapter I].

Definition 1. For a perfect field k with a fixed algebraic closure k^¯, an affine space over k, namely Aⁿ, is defined as the set of n-tuples

.

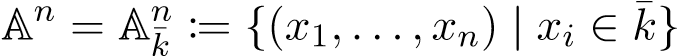The K-rational points of Aⁿ is the set Aⁿ(K) := {(x₁,...,x_n) ∈ Aⁿ | x_i ∈ K} if the field extension k ⊂ K ⊂ k^¯ is an algebraic extension. An affine variety X = V(I) ⊂ Aⁿ is defined over k if the defining ideal I ⊆ k^¯[x₁,...,x_n] is prime and could be generated by polynomials in k[x₁,...,x_n]. The K-rational points of X are then defined by X(K) := X ∩ Aⁿ(K).

In a similar manner, the projective space over k is defined as

,

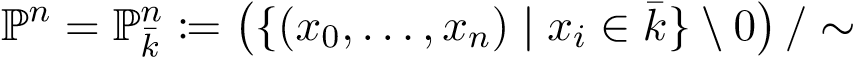where (x₀,...,x_n) ∼ (y₀,...,y_n) if and only if there exists some λ ∈ k^¯× such that y_i = λx_i. The K-rational points of Pⁿ is the set Pⁿ(K) := {[x₀,...,x_n] ∈ Pⁿ | x_i ∈ K}. A projective variety X = V(I) ⊂ Pⁿ is said defined over k if the defining homogeneous ideal I ⊂ k^¯[x₀,...,x_n] is prime and could be generated by homogenous polynomials in k[x₀,...,x_n]. Furthermore, we define the K-rational points of X as the set X(K) := X ∩ Pⁿ(K).

Definition 2 ([2, Section 26]). Let X be an algebraic variety over finite field Fq, denote X(Fqr) as the Fqr-rational points of X. The zeta function of X is a generating function involving the number of these rational points:

.

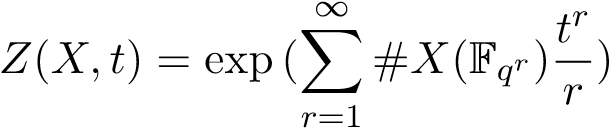Note that Z(X,t) is a formal power series in Q[[t]].

Remark. Since X could be covered by finitely many affine open subsets, we can only describe X(Fqr) in affine case which is more explicit: If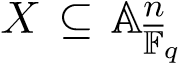 is defined by the ideal (f₁,...,f_d) ⊆

Fq[x₁,...,x_n], then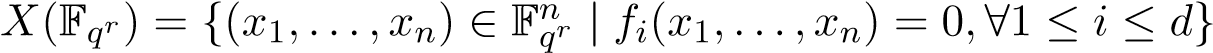

Example 3. Here we give an easy but concrete example to help us have an intuitive feeling about the zeta function. Suppose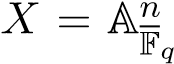, it’s clear from the remark above, that #X(Fqr) is just the number of points in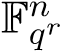. We conclude that

.

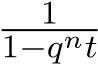In general, for the projective case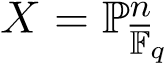, we can obtain

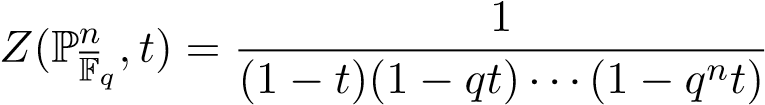
via identifying .

As illustrated in the above example, zeta functions exhibit rationality for affine and projective spaces. More generally, Weil’s conjectures reveal that rationality is a property satisfied by a broad class of varieties.

Theorem 4 (Weil conjectures [3, Section 2.4]). Suppose X is a smooth projective variety over Fq with dim(X) = n, then it has the following properties

(Rationality): Z(X,t) ∈ Q(t), i.e., the zeta function of X is a rational function.

(Functional equation): if E = (∆²) is the self-intersection number of the diagonal ∆ ⊆ X × X, then

.

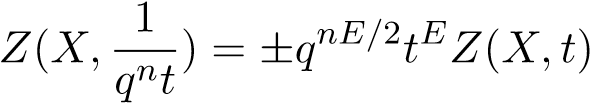Here, E is also known as the Euler-Poincaré characteristic and denoted as χ in some references.

(Analogue of Riemann hypothesis): We can rewrite Z(X,t) as

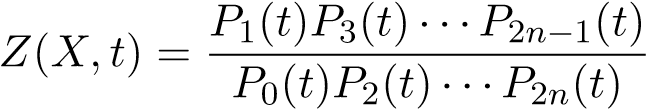
where P₀(t) = 1 − t, P_2n(t) = 1 − qⁿt. Moreover, for all 1 ≤ i ≤ 2n − 1, there exists algebraic integers α_i,j with absolute value q^i/2 such that P_i(t) = ^Q_j(1 − α_i,jt)

(Betti number): Define the ith Betti number of X as bi(X) := deg(Pi(t)). Then we have 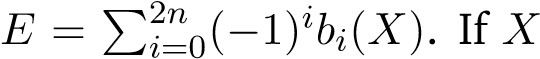is a reduction of a variety Y defined over the ring of integers of a number field K (so its ring of integers denoted as OK) modulo a prime ideal, then bi(X) is equal to ith Betti number of the analytification of Y ×spec(OK) spec(C).

The proof of the Weil conjectures was achieved through a series of developments, ultimately culminating in Pierre Deligne’s proof in 1974. Initially, Weil himself established rationality for specific cases such as curves and abelian varieties [4]. Dwork successfully proved both rationality (general case) and functional equation in 1960 using p-adic analysis method, see [5]. Inspired by algebraic topology and the Lefschetz fixed point theorem, Weil proposed that the conjectures may follow from an appropriate cohomology theory for varieties over finite fields, with coefficients in characteristic-zero field. However, the proof for other two statements was still open until around 1965, Grothendieck and Artin introduced ℓ-adic cohomology (a variant of étale cohomology) based on the initial ideals of Serre, in order to tackle with rationality, functional equation and Betti number. The general property of étale cohomology allowed Grothendieck to give a Lefschetz fixed-point formula for ℓ-adic cohomology. Finally, building on these developments, Deligne gave the proof for the analogue of Riemann hypothesis in 1974 [6]. As we have seen, the effort to prove these conjectures led to the development of new areas in mathematics, including étale cohomology and ℓ-adic cohomology. Although these topics go beyond the scope of this thesis, interested readers may refer to [7] (SGA) by Grothendieck for a comprehensive introduction.

3. Weil cohomology

Although we will not delve into the details of étale cohomology, this section will present a broader perspective on cohomology theories. The Weil cohomology theory is a general concept of cohomology like ℓ-adic one, it’s a certain class of cohomology theories that satisfy some axioms (resembling from singular cohomology over C). One of the most crucial properties of it is the existence of the Lefschetz trace formula (let’s use this name to replace "Lefschetz fixed-point theorem" to emphasize trace). We’ll also see how the rationality followed easily after applying the Lefschetz trace formula. First, let’s state the definition of Weil cohomology, which can be found in [8], [9] or [3] modulo some simplifications.

Definition 5. A Weil cohomology theory is a family of contravariant functors

Hⁱ : {smooth projective variety over k} −→ {K − vector space},i ∈ Z

where k, K are fixed fields such that k is algebraically closed and char(K) = 0. Also, we denote H^∗(X) as the graded K-vector space ^L_i≥0 Hⁱ(X), denote f^∗ as the induced (grad-preserving) morphism given by f. Moreover, there are some given data (For the smooth projective varieties X, Y appear below, assume dim(X) = n, dim(Y ) = m.)

(D1) (Cup product) There exists a map ⌣: Hⁱ(X)×H^j(X) → H^i+j(X) for any i,j makes H^∗(X) a graded-commutative K-algebra, i.e., a ⌣ b = (−1)^ijb ⌣ a if a ∈ Hⁱ(X),b ∈ H^j(X). (By an abuse of the notation, we write ⌣ (a,b) as a ⌣ b.)

(D2) (Trace map) There exists a linear trace map Tr_X : H²ⁿ(X) → K.

(D3) (Cohomology class of cycles) For any closed subvariety Z ⊂ X of codimension c, there is a cohomology class cl(Z) ∈ H^2c(X) given to Z.

Furthermore, these data should satisfy a sequence of axioms

(A1) (Finiteness) Any Hⁱ(X) is finite-dimensional as a K-vector space. In addition, H^j(X) = 0 if j /∈ [0,2n].

(A2) (Poincaré duality) The trace map Tr_X is an isomorphism. For 0 ≤ i ≤ 2n, the composition

Tr_X◦ ⌣: Hⁱ(X) × H²ⁿ⁻ⁱ(X) −→ K,(a,b) 7−→ Tr_X(a ⌣ b)

is K-bilinear and a perfect pairing.

(A3) (Künneth formula) Let p_X,p_Y be the projective map from X × Y to X,Y respectively. The cup product then induces a K-algebra homomorphism

which is required to be an isomorphism.

(A4) (Case of a point) For P = spec(k), then cl(P) = 1 and Tr_P (1) = 1.

(A5) (Compatibility of trace map and cup product) For any a ∈ H²ⁿ(X),b ∈ H^2m(Y ),

Tr_X×_Y (p^∗_Xa ⌣ p^∗_Y b) = Tr_X(a) · Tr_Y (b).

This indicates that the trace map is multiplicative with respect to cup product.

(A6) (Exterior product of cohomology classes) If Z ⊂ X,W ⊂ Y are closed subvarieties, then

cl(Z × W) = p^∗_X(cl(Z)) ⌣ p^∗_Y (cl(W)).

Here, is obtained from cl(Z)⊗ cl(W) via the map defined in (A3).

So, (A6) actually says the class map should be compatible with the Künneth formula.

(A7) (Push-forward of cohomology classes) Let f : X → Y be a morphism between X and Y . If Z ⊂ X is a closed subvariety, then for any class ω ∈ H^2m(Y ) one has

Tr_X(cl(Z) ⌣ f^∗(ω)) = deg(Z/f(Z))Tr_Y (cl(f(Z)) ⌣ ω).

(A8) (Pull-back of cohomology classes) If morphism f : X → Y and closed subvariety W ⊂ Y satisfying :

f−(W) has pure dimension dim(W)+n−m, i.e., all irreducible components Z1,...,Zr of f−1(W) have dimension dim(W) + n − m

Either f is flat in an open neighbourhood of W, or W is generically transverse to f, i.e., f−1(W) is generically reduced.

Also, assume [f⁻¹(W)]¹ = ^Pr_i=1 m_iZ_i as a cycle of codimension m − dim(W), then

r

f^∗(cl(W)) = ^Xm_icl(Z_i).

i=1

Remark. From the definition of Weil cohomology, we know f^∗ acts as a pull-back map on the cohomology group when f is a morphism between smooth projective varieties X,Y with dimension n,m respectively. We can also define a push-forward map for f using Poincaré duality. For ω ∈ Hⁱ(X), we define f_∗ω ∈ H^2m−2n+i(Y ) such that

Tr_Y (f_∗ω ⌣ µ) = Tr_X(ω ⌣ f^∗µ)

for any µ ∈ H²ⁿ⁻ⁱ(Y ). Note this definition is well-defined due to the Poincaré duality. Indeed, as Tr_X(ω ⌣ f^∗(·)) ∈ Hom(H²ⁿ⁻ⁱ(Y ),K), uniqueness of f_∗ω is given by the isomorphism H2m−2n+i(Y ) ∼= Hom(H2n−i(Y ),K).

Those familiar with differential topology may notice several parallels between Weil cohomology and classical de Rham cohomology on compact manifolds. For instance, [ω] ⌣ [µ] = [ω ∧ µ] for [ω] ∈ H_dRⁱ (M),[µ] ∈ H_dR^j (M) for ω,µ on a compact smooth manifold M. The trace map could be interpreted as the integration map: ω 7→ ^R_M ω. It is remarkable that if X is a smooth projective variety over some field k embedded in C, then X(C) could be regarded as a compact complex manifold [11]. Next we give some famous examples of Weil cohomology.

Example 6. The first basic example of Weil cohomology is the singular cohomology over C. Moreover, one may expect an analogy of de Rham theorem, if k = C, then the algebraic de

Rham cohomology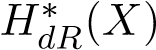 is isomorphic to singular cohomology of analytification of X, we refer this to Grothendieck’s work [12]. In general, if char(X) = 0, the algebraic de Rham cohomology of X is always a Weil cohomology [13]. Later, we’ll define what’s an algebraic de Rham cohomology for smooth affine varieties and see how it fails to be a well-behaved cohomology when char(k) > 0.

Example 7 ([14]). For the case char(k) > 0, one classical Weil cohomology is the ℓ-adic cohomology, where ℓ is a prime different with char(k) and K = Qℓ.

3.1. Lefschetz trace formula

Now, it’s time to present our Lefschetz trace formula, which is a key result in Weil cohomology theory. Roughly speaking, it states that the number of fixed points of an endomorphism on X could be represented as the alternating sum of the traces of induced linear map on cohomology groups.

Theorem 8 (Lefschetz trace formula). Let X be a smooth projective variety of dimension n and let f : X → X be an endomorphism, then for any Weil cohomology H^∗, we have

,

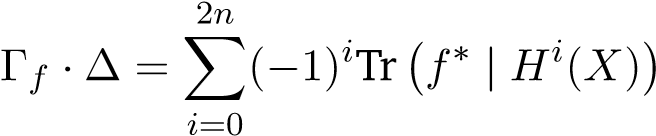where ∆ = {(x,y) ∈ X × X | x = y} denote the diagonal, Γ_f = {(x,f(x)) ∈ X × X | x ∈ X} denote the graph of f.

Remark. Here Γ_f · ∆ represents the intersection number (counted with multiplicities) of the graph and the diagonal. In particular, if they intersect transversely, this number is euqal to |{x ∈ X | f(x) = x}|, the count of fixed points by f.

While the proof of the trace formula is somewhat tedious and involved, it is worthwhile to go through it as it provides a deeper understanding of Weil cohomology. We will divide the proof into several steps. First, establish some useful lemmas derived from the definition of Weil cohomology. These can also be found in de Jong’s note [9].

Lemma 9. Assume X,Y are smooth projective varieties over k with dimension n,m respectively and f : X → Y is an arbitrary morphism. H^∗ is any Weil cohomology over a field K. Then the following properties valid.

The K-algebra homomorphism K → H0(X) given by K-algebra structure is an isomorphism. Hence, if α ∈ H0(X),β ∈ Hi(X), α ⌣ β = α · β by regarding α as an element in K.

cl(X) = 1 ∈ H0(X).

f∗(α ⌣ f∗γ) = f∗α ⌣ γ for any α ∈ Hi(X),γ ∈ Hj(Y ). It’s also called the projection formula.

For any closed subvariety Z ⊂ X, f∗(cl(Z)) = deg(Z/f(Z)) · cl(f(Z)).

For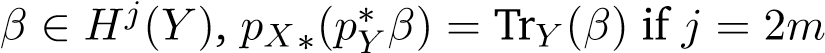, and equal to 0 otherwise.

For α ∈ Hi(X), one has

where p₁,p₂ are the projections from X ×X to the first and the second coordinate, respectively.

Proof. (i). Using (A2) (Poincaré duality) for i = 0, we obtain H⁰(X) ^∼= (H²ⁿ(X))^∗. Since Tr_X is an isomorphism, we get dim_K(H²ⁿ(X)) = dim_K(K) = 1. Hence, the dimension of H⁰(X) is also 1. Moreover, the map K → H⁰(X) is injective since K is a field, hence bijective. (ii). Applying (A8) to the obvious map p : X → spec(k), we obtain cl(X) = p^∗(cl(spec(k))) = 1 as cl(spec(k)) = 1 by (A4).

(iii). First, by the definition of push-forward of f, we know Tr_Y (f_∗(α ⌣ f^∗γ) ⌣ β) = Tr_X((α ⌣ f^∗γ) ⌣ f^∗β) for any β ∈ H^2n−(i+j)(Y ). Using the associativity and the definition of pushforward again, we have

Tr_X((α ⌣ f^∗γ) ⌣ f^∗β) = Tr_X(α ⌣ (f^∗γ ⌣ f^∗β)) = Tr_Y (f_∗α ⌣ (γ ⌣ β)) = Tr_Y ((f_∗α ⌣ γ) ⌣ β).

Therefore, for any β ∈ H^2n−(i+j)(Y ), Tr_Y (f_∗(α ⌣ f^∗γ) ⌣ β) = Tr_Y ((f_∗α ⌣ γ) ⌣ β). We conclude f_∗(α ⌣ f^∗γ) = f_∗α ⌣ γ via (A2).

(iv) The proof is almost the same as (iii) and use (A7) for the middle step.

(v). Note p_X∗(p^∗_Y β) ∈ H^j−2m(X). So, (A1) tells us that p_X∗(p^∗_Y β) = 0 automatically once j ̸= 2m. Indeed, if j < 2m, H^j−2m(X) = 0; if j > 2m, H^j(Y ) = 0 and then β = 0. For the case j = 2m, p_X∗(p^∗_Y β) ∈ H⁰(X) ^∼= K. Therefore, for any α ∈ H²ⁿ(X), one has p_X∗(p^∗_Y β) · Tr_X(α) = Tr_X(p_X∗(p^∗_Y β) ⌣ α) = Tr_X×_Y (p^∗_Y β ⌣ p^∗_Xα) = Tr_Y (β) · Tr_X(α).

The first equality follows by the linearity of trace map and (i); the second one comes from the definition of push-forward of p_X∗; the last one just by (A5). It follows that p_X∗(p^∗_Y β) = Tr_Y (β). (vi). Define φ : X ,→ X × X,x 7→ (x,f(x)) as the embedding of the graph of f. Clearly p₁ ◦ φ = id_X,p₂ ◦ φ = f. Moreover, as φ is an isomorphism between X,Γ_f, deg(X/φ(X)) = 1.

It follows that φ_∗(cl(X)) = cl(Γ_f) by (iv). Therefore,

Note the second equality given by (iii) and the last two just follow from the functoriality of H^∗ and cl(X) = 1.

With these properties of Weil cohomology, we can now proceed with linear algebra manipulations.

Proposition 10 (Lemma 4.10, [3]). Following the setting in Theorem 8. Let {w_j^2n−r}_j=1,...,kr be a basis for H^2n−r(X), ∀r. Thanks to Poincaré duality (A2), we know H^r(X) ^∼= (H^2n−r(X))^∗ via the map ω 7→ Tr_X((·) ⌣ ω). Therefore, there exists a dual basis {v_i^r}_i=1,...,kr for H^r(X) such that Tr_X(w_j^2n−r ⌣ v_i^r) = δ_i,j. Under these assumptions, we have

cl.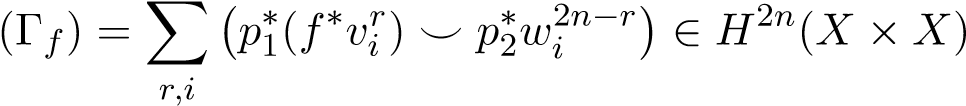

Proof. Using the Künneth formula (A3), it allows us to write cl(Γ_f) in the following way:

cl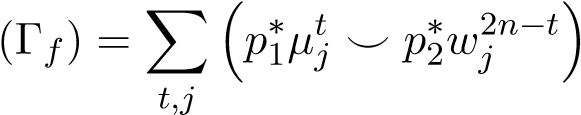

for some unique µ^t_j ∈ H^t(X). Indeed, as cl(Γ_f) ∈ H²ⁿ(X × X), (A3) shows each term of cl(Γ_f) comes from µ ⊗ ω ∈ H^t(X) ⊗ H^2n−t(X),∀t. As we already fix a basis {w_j^2n−t} for H^2n−t(X), each µ^t_j is unique clearly. On the other hand, using Lemma 9 (iii), (vi) and substitute cl(Γ_f), we obtain

for any fixed r and i. One remarkable is that in order to use (iii), we should commute the terms for both sides of the third equality. Now, using Lemma 9 (v), we know

if t ̸= r and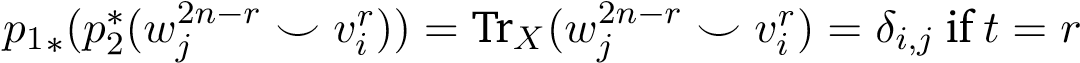. Hence, f^∗v_i^r = ^P_j δ_ij(µ^r_j) = µ^r_i , we’re done.

Before moving to the final proof of the Lefschetz trace formula, we need one last piece from algebraic geometry. We’ll just state and use it without proof.

Lemma 11 (Corollary 4.6, [3]). Let X be a smooth projective variety, if α_i ∈ Aⁿⁱ(X) for i =

1,...,k such that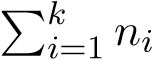= dim(X). Then, the intersection number of α_i

α₁ · ... · α_k = Tr_X(cc(α₁) ⌣ ... ⌣ cc(α_k))

where cc is the cycle class map.

Finally, we conclude the proof of the Lefschetz trace formula with these elements.

Proof. (of Theorem 8) Recall the Proposition 10, for any t, if we replace the basis of H^t(X) by

{w_j^t}_j=1,...,kt, then the corresponding dual basis in H^2n−t(X) should be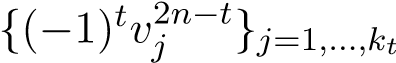 due to the graded-commutativity of H^∗(X). It follows a similar result with Proposition 10, apply it to f = id_X we obtain cl .

Using Lemma 11 and substitute cl(∆), cl(Γ_f) we have

Γ_f · ∆ = Tr_X×X(cl(Γ_f) ⌣ cl(∆))

= TrX×X X (−1)t+t(2n−r)p∗1(f∗vir ⌣ wjt) ⌣ p∗2(wi2n−r ⌣ vj2n−t)

r,t,i,j

= X TrX(f∗vir ⌣ wi2n−r) · TrX(wi2n−r ⌣ vir) = X TrX(f∗vir ⌣ wi2n−r).

r,ir,i

The third equality holds by observing that the terms with t ̸= 2n−r,j ̸= i are vanishing via (A1) and Tr_X(w_j^2n−r ⌣ v_i^r) = δ_i,j. Fix r, assume for some λ_i,s ∈ K, then

,

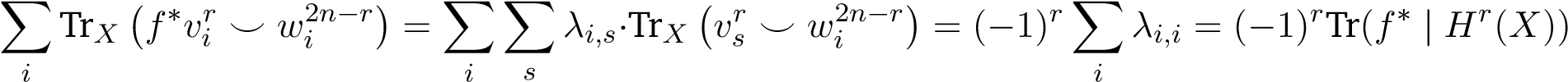where the second equation follows from Tr 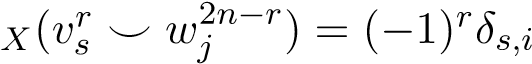. We’re done!

This leads us to an immediate application of the Lefschetz trace formula in proving the rationality aspect of the Weil conjecture.

Theorem 12. Assume φ : X → X is the q-power Frobenius endomorphism of smooth projective variety X with dimension n over Fq, then

.

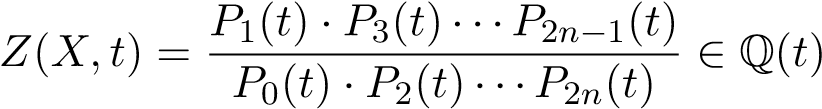where P_i(t) = det(1 − tHⁱ(φ))⁻¹. (Hⁱ(φ) is an abbreviation for (φ^∗ | Hⁱ(X)).)

Proof. Some simple field theories tell us that Fqr could be described as the subfield of Fq that fixed by r many q-power Frobenius automorphism, i.e., Fqr = {x ∈ Fq | x^qr = x}. Therefore,

#X(Fqr) = |{x ∈ X | φ^r(x) = x}| = Γ_φr · ∆,

the second equality is given by the fact that the graph of φ^r intersects transversely with the diagonal, see [3, Prop. 2.4]. Apply Lefschetz trace formula and substitute into the zeta function, one may expect

.

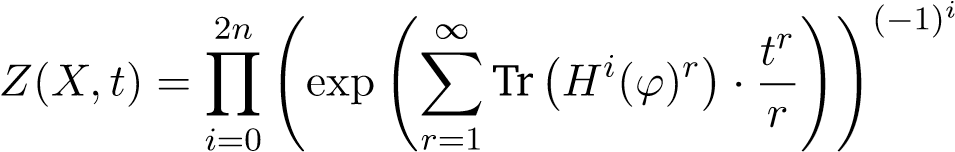To conclude, we need a lemma from linear algebra: Let F be a linear endomorphism over a finite dimensional K-vector space V for some field K, then .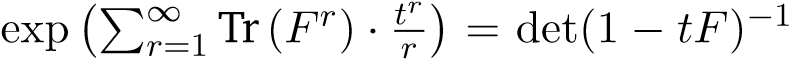

To see this, we induct on dim(V ). The case dim(V ) = 1 is trivial. For the general case, note we can always assume K is algebraically closed since the lemma doesn’t depend on the ground field. Therefore, we can assume F has an eigenvector v ∈ V and then rewrite the matrix of F as a block matrix M₁ ⊕ M₂, where M₁ is the matrix for F|_span(v) and M₂ is the one for F|_V/span(v). By the inductive hypothesis,

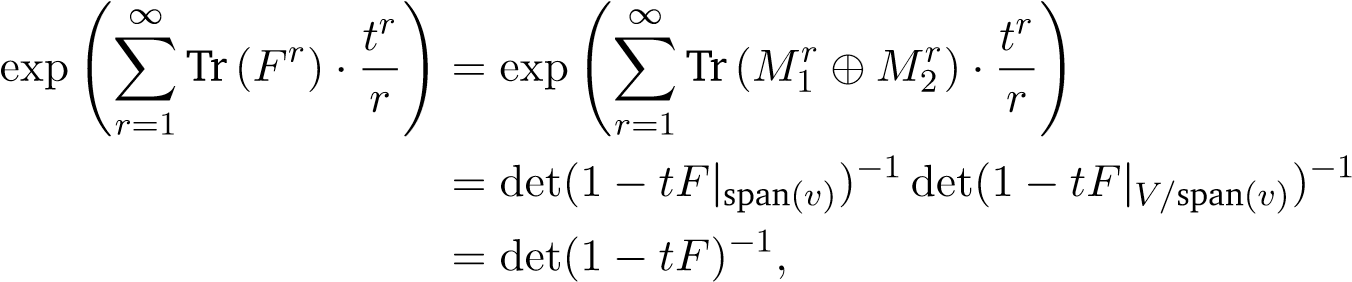
the lemma is proved. Finally, substitute F with Hⁱ(φ), the theorem then follows by our lemma.

4. Conclusion

In this thesis, we explored the Weil conjecture and its profound implications for algebraic geometry, particularly through the application of Weil cohomology theories and the Lefschetz trace formula. By bridging the arithmetic properties of varieties over finite fields with topological concepts, the Weil conjecture has reshaped our understanding of cohomology, zeta functions, and their interconnections. The Lefschetz trace formula, in particular, provides a powerful mechanism for point-counting, revealing the intricate structure of rational points on varieties. This foundational framework not only contributed to Pierre Deligne’s proof of the Riemann Hypothesis for varieties over finite fields but also catalyzed the development of new cohomological techniques that continue to influence research in number theory and algebraic geometry.