1. Introduction
H-matrices have wide applications in numerical analysis, control theory, matrix theory and statistics [1-4]. An important method to study the properties of H-matrices is to consider its subclasses. H-matrices include many well-known subclasses, such as strictly diagonally dominant (SDD) matrices, doubly strictly diagonally dominant (DSDD) matrices, Σ-SDD matrices, γ-SDD matrices, weakly chained diagonally dominant matrices, Nekrasov matrices, Σ-Nekrasov matrices,
Dashnic Zusmanovich (DZ) matrices and eventually SDD matrices.
The class of Dashnic-Zusmanovich type (DZT) matrices were introduced by Zhao et al. in2018 [5]. They proved that DZT matrices belong to the class of H-matrices. Many results about DZT matrices have been obtained. One can refer to [6-9].
This paper introduces a new matrix subclass:
2. Preliminaries
We use
If
Definition 2.1. Let
Definition 2.2.Let
Definition 2.3. Let
Definition 2.4.Let
3. Main results
Definition 3.1. A matrix
We say that A is a
It is easy to see that
Let
Theorem 3.1. Let
Proof. Let
Case 1.
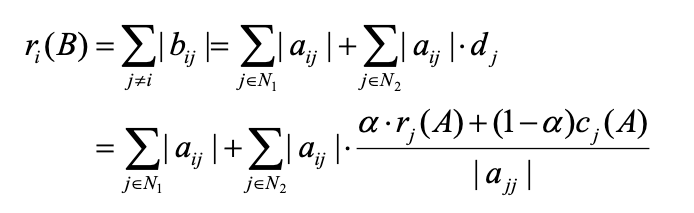
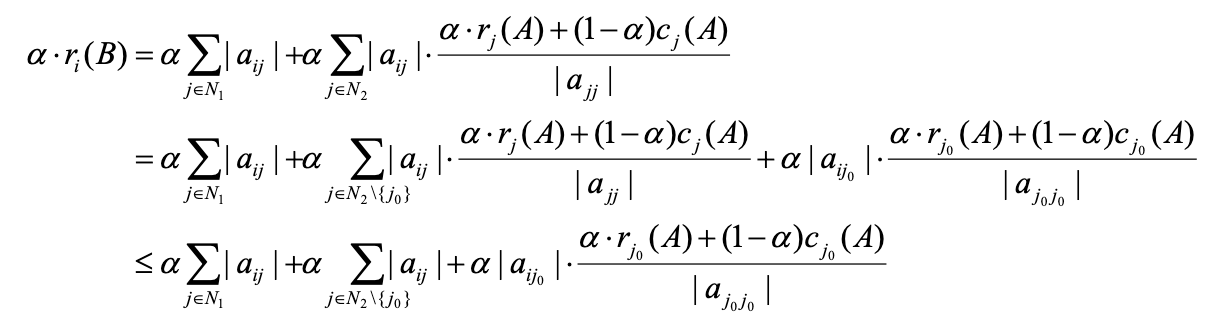
Because
then
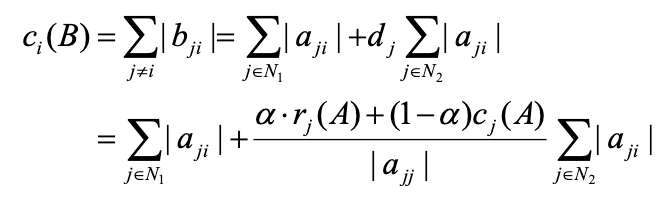
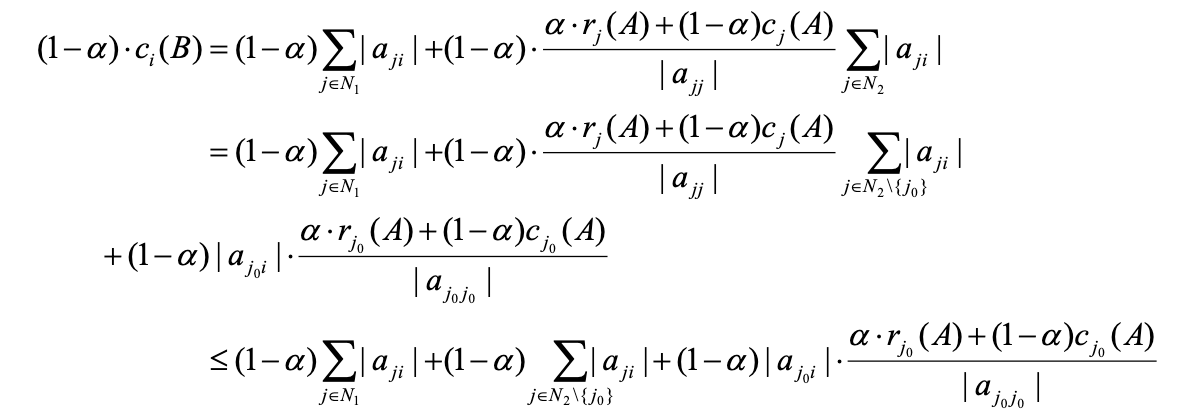
Because
,
then
and because of formula (3.2),
we proved
Case 2.
and
The above formula can be expanded to get
,
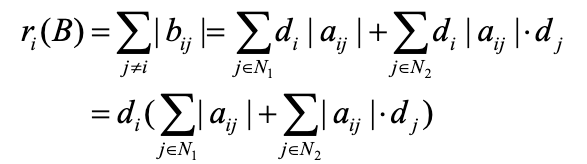
And,

Solving simultaneously, we get
then
Theorem 3.2. A matrix
Proof. If A is a DZT matrix, then A is a 1-DZT matrix. Now we show that if A is an
First of all, by definition, it is obvious that if matrix A belongs to SDD matrix, then A must belong to
By definition, if the hypothesis
Because
For the argument, we also use the reverse order method, assuming that the conclusion
Eliminate the common terms on both sides of the inequality at the same time.
In the same way, because
For the proof of theorem 2, we mainly use the core idea of reverse order. We start with the result we want to prove, analyze what conditions are needed to get that result, and then work our way forward to see how we can obtain these conditions from what we already know. Thus, we prove the relationship between SDD, DZT,
4. Conclusion
This paper successfully introduces a new subclass of matrices, the
References
[1]. J. Liu, Y. Huang, Some properties on Schur complements of H-matrices and diagonally dominant matrices, Linear Algebra Appl. 389 (2004) 365-380.
[2]. J. Liu, J. Li, Z. Huang, X. Kong, Some properties of Schur complements and diagonal-Schur
[3]. R. Smith, Some interlacing properties of the Schur complement of a Hermitian matrix, Linear
[4]. C. Li, Z. Huang, J. Zhao, On Schur complements of Dashnic-Zusmanovich type matrices, Linear Mutilinear Algebra 70 (2022) 4071-4096.
[5]. J. Zhao, Q. Liu, C. Li, et al. Dashnic-Zusmanovich type matrices: a new subclass of nonsingular H-matrices [J]. Linear Algebra and its Applications, 2018, 552: 277–287.
[6]. C. Li, L. Cvetkovic, Y. Wei, et al. An infinity norm bound for the inverse of Dashnic–Zusmanovich type matrices with applications [J]. Linear Algebra and its Applications, 2019, 565: 99–122.
[7]. W. Zeng, J. Liu, H. Mo, Schur complement-based infinity norm bound for the inverse of Dashnic-Zusmanovich type matrices [J]. Mathematics, 2023, 11(10): 2254.
[8]. P. Dai, D. Pan. Subdirect sum of Dashnic-Zusmanovich type matrices [J]. Chinese journal of engineering mathematics, 2022, 39(06): 979–996.
[9]. L. Liu, X. Chen, Y. Li, et al. Subdirect sums of Dashnic-Zusmanovich matrices [J]. Bulletin des Sciences Mathématiques, 2021, 173: 103057.
Cite this article
Delun,L.;Shiyun,W.;Changyue,L.;Airu,S.;Bo,J. (2025). A New Subclass of H-matrices:γ-DZT Matrices. Theoretical and Natural Science,104,1-5.
Data availability
The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.
Disclaimer/Publisher's Note
The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
About volume
Volume title: Proceedings of CONF-MPCS 2025 Symposium: Mastering Optimization: Strategies for Maximum Efficiency
© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and
conditions of the Creative Commons Attribution (CC BY) license. Authors who
publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons
Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this
series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published
version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial
publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and
during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See
Open access policy for details).
References
[1]. J. Liu, Y. Huang, Some properties on Schur complements of H-matrices and diagonally dominant matrices, Linear Algebra Appl. 389 (2004) 365-380.
[2]. J. Liu, J. Li, Z. Huang, X. Kong, Some properties of Schur complements and diagonal-Schur
[3]. R. Smith, Some interlacing properties of the Schur complement of a Hermitian matrix, Linear
[4]. C. Li, Z. Huang, J. Zhao, On Schur complements of Dashnic-Zusmanovich type matrices, Linear Mutilinear Algebra 70 (2022) 4071-4096.
[5]. J. Zhao, Q. Liu, C. Li, et al. Dashnic-Zusmanovich type matrices: a new subclass of nonsingular H-matrices [J]. Linear Algebra and its Applications, 2018, 552: 277–287.
[6]. C. Li, L. Cvetkovic, Y. Wei, et al. An infinity norm bound for the inverse of Dashnic–Zusmanovich type matrices with applications [J]. Linear Algebra and its Applications, 2019, 565: 99–122.
[7]. W. Zeng, J. Liu, H. Mo, Schur complement-based infinity norm bound for the inverse of Dashnic-Zusmanovich type matrices [J]. Mathematics, 2023, 11(10): 2254.
[8]. P. Dai, D. Pan. Subdirect sum of Dashnic-Zusmanovich type matrices [J]. Chinese journal of engineering mathematics, 2022, 39(06): 979–996.
[9]. L. Liu, X. Chen, Y. Li, et al. Subdirect sums of Dashnic-Zusmanovich matrices [J]. Bulletin des Sciences Mathématiques, 2021, 173: 103057.









