1. Introduction

Singular Value Decomposition (SVD) is a fundamental matrix factorisation technique in linear algebra, generalizing eigenvalue decomposition to non-square and non-symmetric matrices. It decomposes any real or complex matrix into one or more matrices whose size is less than the original one A of size m×n into three matrices, providing deeper insights into structural properties such as rank, nullity, and geometric transformations [1]. SVD has wide applications in different areas, such as signal processing, data compression, machine learning, and computer vision. It is particularly valuable for solving least squares problems, reducing dimensionality, and reducing noise on datasets. It also finds applications in principal component analysis (PCA), search algorithms, and image processing. This paper discusses the mathematical foundations of SVD, its geometric interpretation, existence, and uniqueness [2]. The differences between SVD and eigenvalue decomposition and some practical use of it in python are discussed. The real-world use, the applications of SVD, such as image compression and reductions of data dimensionality are also discussed.

As for basic concepts:

1. Symmetric Matrix: A matrix A is called symmetric when it is equal to its transpose.

Example: A =  $$ \left[\begin{array}{ccc}1& 2& 3\\ 2& 4& 5\\ 3& 5& 6\end{array}\right]$$ 

2. Eigenvalue Decomposition: A symmetric n×n matrix ‘A’ having ‘n’ real eigenvalues and an orthonormal basis of eigenvectors can be expressed as:

$$ {\mathrm{A}\mathrm{ }=\mathrm{ }\mathrm{V}\mathrm{\Lambda }\mathrm{V}}^{-1}$$(1)

Here, V is the matrix with columns as eigenvectors, and Λ is the diagonal matrix with eigenvalues as diagonal elements. This is called eigenvalue decomposition [3].

3. Singular Value Decomposition: This is a generalisation of eigenvalue decomposition with the requirement that the matrix is not necessarily symmetric or even square. A matrix 'A' can be represented in the form of a matrix factorization of order m × n [4]. It is a linear algebra method of decomposition of a real or complex matrix into three matrices

Before studying it in detail, an exploration of the components of Singular Value Decomposition (SVD) is presented.

2. Geometric interpretation of SVD

The SVD is geometrically seen as the fact that the image of the unit sphere under any m x n matrix is a hyperellipse [5]. The SVD is applicable to both real and complex matrices. However, in describing the geometric interpretation, it is usually assumed that the matrix is real.

The term "hyperellipse" represents an unfamiliar way of describing m-dimensional ellipses within their generalized format. A hyperellipse in  $$ {\mathbb{ℝ}}^{\mathrm{m}}$$  is formed by stretching the  $$ {\mathbb{ℝ}}^{\mathrm{m}}$$  unit sphere with factors  $$ {\mathrm{\sigma }}_1,\dots ,{\mathrm{\sigma }}_{\mathrm{m}}$$  (maybe zero) in the orthogonal directions  $$ {\mathrm{u}}_1,\dots ,{\mathrm{u}}_{\mathrm{m}}\in {\mathbb{ℝ}}^{\mathrm{m}}$$ . The vectors  $$ {\mathrm{u}}_{\mathrm{i}}$$  are unit-length vectors since $$ {\Vert {\mathrm{u}}_{\mathrm{i}}\Vert }_2=1$$ . The vectors { $$ {\mathrm{\sigma }}_{\mathrm{i}}{\mathrm{u}}_{\mathrm{i}}$$  } function as the principal semiaxes of the hyperellipse, delivering the lengths $$ {\mathrm{\sigma }}_1,\dots ,{\mathrm{\sigma }}_{\mathrm{m}}$$ . When A achieves rank r, then exactly r of the  $$ {\mathrm{\sigma }}_{\mathrm{i}}$$  will become non-zero values, and in this context, when m has a minimum value of n, the maximum allowed number of non-zero  $$ {\mathrm{\sigma }}_{\mathrm{i}}$$  will equal n [6]. The unit sphere refers to the Euclidean sphere standard in n-space while using the 2-norm definition; thus, it is denoted as S. Through the transformation A, the image of S contains the shape of a hyperellipse that is defined.

Let A ∈  $$ {\mathbb{ℝ}}^{\mathrm{m}\times \mathrm{n}}\mathrm{ }$$ and consider A maps an input vector in 𝐴 ∈ $$ {\mathbb{ℝ}}^{\mathrm{n}}$$  to an output vector in  $$ {\mathbb{ℝ}}^{\mathrm{m}}$$ .

Let  $$ \mathrm{V}=\left\{{\mathrm{v}}_1,\cdots ,{\mathrm{v}}_{\mathrm{n}}\right\}$$  be an orthonormal matrix of  $$ {\mathbb{ℝ}}^{\mathrm{n}}$$ 

Let  $$ \mathrm{U}=\left\{{\mathrm{u}}_1,\cdots ,{\mathrm{u}}_{\mathrm{m}}\right\}$$  be an orthonormal matrix of  $$ {\mathbb{ℝ}}^{\mathrm{m}}$$ 

Let  $$ \left\{{\mathrm{\sigma }}_1,\cdots ,{\mathrm{\sigma }}_{\mathrm{m}}\right\}$$  be a set of  $$ \mathrm{m}$$  scalars with  $$ {\mathrm{\sigma }}_{\mathrm{i}}\ge 0,\mathrm{i}=1,\cdots \mathrm{m}$$ 

Then,  $$ {\mathrm{\sigma }}_{\mathrm{i}}{\mathrm{\mu }}_{\mathrm{i}}$$  is the  $$ \mathrm{i}$$  th principal semiaxis with length  $$ {\mathrm{\sigma }}_{\mathrm{i}}$$  in  $$ {\mathbb{ℝ}}^{\mathrm{m}}$$ .

Now, if  $$ \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left(\mathrm{A}\right)=\mathrm{r}$$ , then exactly  $$ \mathrm{r}$$  of  $$ \left\{{\mathrm{\sigma }}_1,\cdots ,{\mathrm{\sigma }}_{\mathrm{m}}\right\}$$  are nonzero and exactly  $$ \mathrm{m}-\mathrm{r}$$  of  $$ {\mathrm{\sigma }}_{\mathrm{i}}$$  's we zero.So, if  $$ \mathrm{m}\ge \mathrm{n}$$ , then  $$ \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left(\mathrm{A}\right)\le \mathrm{n}$$  i.e., at most  $$ \mathrm{n}$$  of  $$ {\mathrm{\sigma }}_{\mathrm{i}}$$  's are nonzero.

For simplicity, let's assume  $$ \mathrm{m}\ge \mathrm{n}$$  and  $$ \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left(\mathrm{A}\right)=\mathrm{n}$$ 

Definition 1: The singular values are the lengths of the  $$ \mathrm{n}$$  principal semiaxes of the hyperellipsoid  $$ \mathrm{A}\mathrm{S}$$ (As shown in Figure 1)

The convention is:  $$ {\mathrm{\sigma }}_1\ge {\mathrm{\sigma }}_2\ge \cdots \ge {\mathrm{\sigma }}_{\mathrm{n}}>0$$ 

Definition 2: The  $$ \mathrm{n}$$  left singular vectors of  $$ \mathrm{A}$$  are the unit vectors  $$ \left\{{\mathrm{u}}_1,\cdots ,{\mathrm{u}}_{\mathrm{n}}\right\}$$  in  $$ {\mathbb{ℝ}}^{\mathrm{m}}$$  along the principal semiaxes of  $$ \mathrm{A}\mathrm{S}$$ . So,  $$ {\mathrm{\sigma }}_{\mathrm{i}}{\mathrm{u}}_{\mathrm{i}}$$  is the  $$ \mathrm{i}$$  the largest principal semiaxis of  $$ \mathrm{A}\mathrm{S}$$ .

Definition 3: The  $$ \mathrm{n}$$  right singular vectors of  $$ \mathrm{A}$$  are the unit vectors  $$ \left\{{\mathrm{v}}_1,\cdots ,{\mathrm{v}}_{\mathrm{n}}\right\}\in \mathrm{S}$$  which are the preimages of the principal semiaxes of  $$ \mathrm{A}\mathrm{S}$$ , i.e.,

 $$ \mathrm{A}{\dot{\mathrm{v}}}_{\mathrm{i}}={\mathrm{\sigma }}_{\mathrm{i}}{\mathrm{u}}_{\mathrm{i}}\mathrm{ }\mathrm{i}=1,\cdots ,\mathrm{n}.$$ 

3. Reduced SVD

Consider  $$ \widehat{\mathrm{U}}={\left[\begin{array}{ccc}{\mathrm{u}}_1& \cdots & {\mathrm{u}}_{\mathrm{n}}\end{array}\right]}_{\mathrm{m}\times \mathrm{n}}$$  and  $$ \stackrel{\mathrm{ˆ}}{\mathrm{\Sigma }}={\left[\begin{array}{ccc}{\mathrm{\sigma }}_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathrm{\sigma }}_{\mathrm{n}}\end{array}\right]}_{\mathrm{n}\times \mathrm{n}}$$ 

Consider  $$ {\left[\mathrm{A}\right]}_{\mathrm{m}\times \mathrm{n}}{\left[\begin{array}{ccc}{\mathrm{v}}_1& \cdots & {\mathrm{v}}_{\mathrm{n}}\end{array}\right]}_{\mathrm{n}\times \mathrm{n}}={\left[\begin{array}{ccc}{\mathrm{u}}_1& \cdots & {\mathrm{u}}_{\mathrm{n}}\end{array}\right]}_{\mathrm{m}\times \mathrm{n}}{\left[\begin{array}{ccc}{\mathrm{\sigma }}_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathrm{\sigma }}_{\mathrm{n}}\end{array}\right]}_{\mathrm{n}\times \mathrm{n}}$$ 

So,

AV =  $$ \widehat{\mathrm{U}}\stackrel{\mathrm{ˆ}}{\mathrm{\Sigma }}$$(2)

Now, since V is an orthogonal matrix then:

A =  $$ \widehat{\mathrm{U}}\stackrel{\mathrm{ˆ}}{\mathrm{\Sigma }}{\mathrm{V}}^{\mathrm{T}}$$(3)

4. Full SVD

It is given that  $$ \stackrel{\mathrm{ˆ}}{\mathrm{U}}\in {\mathbb{ℝ}}^{\mathrm{m}\times \mathrm{n}}$$  in the reduced SVD with  $$ \mathrm{m}\ge \mathrm{n}$$ . This implies that the column vectors of  $$ \stackrel{\mathrm{ˆ}}{\mathrm{U}}$$  do not form an ONB of  $$ {\mathbb{ℝ}}^{\mathrm{m}}$$  unless  $$ \mathrm{m}=\mathrm{n}$$ .

 $$ \Rightarrow $$  Remedy: Adjoin  $$ \mathrm{m}-\mathrm{n}$$  ON vectors to  $$ \stackrel{\mathrm{ˆ}}{\mathrm{U}}$$  to form an orthogonal matrix  $$ \mathrm{U}$$ .

Then  $$ \stackrel{\mathrm{ˆ}}{\mathrm{\Sigma }}$$  must be changed to  $$ \mathrm{\Sigma }\in {\mathbb{ℝ}}^{\mathrm{m}\times \mathrm{n}}$$ 

Hence,

$$ \mathrm{A}=\mathrm{U}\mathrm{\Sigma }{\mathrm{V}}^{\mathrm{\top }}$$(4)

This is the full  $$ \mathrm{S}\mathrm{V}\mathrm{D}$$  of  $$ \mathrm{A}$$ 

For non-full rank matrices, i.e.,  $$ \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left(\mathrm{A}\right)=\mathrm{r}<\mathrm{m}\mathrm{i}\mathrm{n}(\mathrm{m},\mathrm{n})$$ , only  $$ \mathrm{r}$$  positive singular values. So,

 $$ \mathrm{\Sigma }=\left[\begin{array}{ccc}{\mathrm{\sigma }}_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathrm{\sigma }}_{\mathrm{n}}\\ \cdots 0& 0& 0\end{array}\right]$$  , in this case  $$ \mathrm{m}\ge \mathrm{n}$$ 

and  $$ \left[\begin{array}{ccccc}{\mathrm{\sigma }}_1& \cdots & 0& :& 0\\ ⋮& \ddots & ⋮& :& 0\\ 0& \cdots & {\mathrm{\sigma }}_{\mathrm{n}}& :& 0\end{array}\right]$$ , in this case  $$ \mathrm{m}\le \mathrm{n}$$ 

when  $$ \mathrm{m}=\mathrm{n}$$  ,. it’s invertible and nonsingular theoretically.

5. Application of SVD

5.1. Image compression

An image is depicted as a matrix where every element corresponds to pixel values.

SVD is applied to decompose the image matrix A into three matrices U, Σ, and  $$ {\mathrm{V}}^{\mathrm{T}}$$  [7]. This makes the largest individual singular values and associated vectors can represent the original image with fewer data, making the file smaller but also resulting in some information loss(As shown in Figure 2).

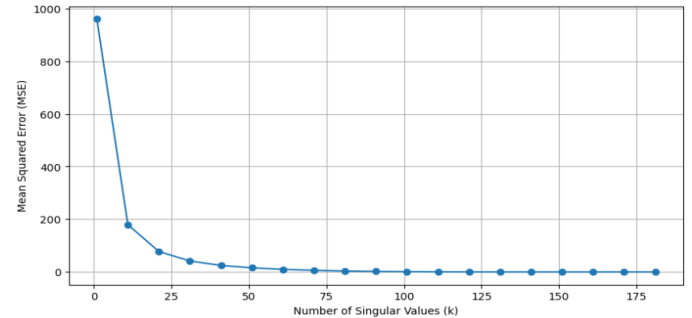
Result: The Figure 3 shows the Mean Squared Error of image restorations against the number of singular values (k) employed in Singular Value Decomposition (SVD). It points to a steep drop in MSE as k is raised from a low value, reflecting considerable improvement in image quality (as shown in Figure 4). The MSE stabilizes as k continues to rise, implying that there are diminishing gains in image quality improvement. Hence, an optimal k value is 175, where image quality meets compression efficiency.

5.2. Data dimensionality reduction

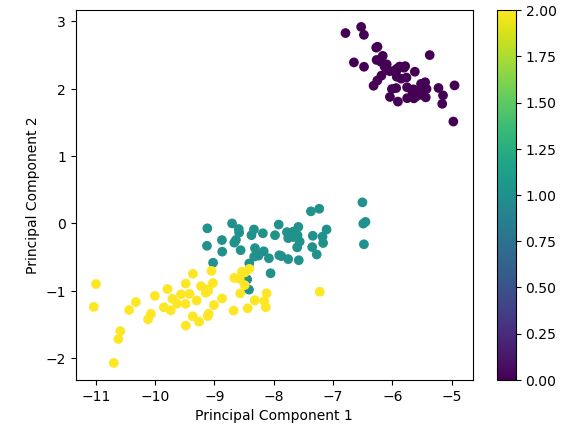
Use SVD to perform dimensionality reduction on a dataset for visualization or further analysis.

SVD compressed the 4D data down into 2D while keeping an important structure.

It works:

1. Exploring high-dimensional data: According to Chiu [8], humans do not have the 3D vision and SVD enables to see that.

2. Use how to improve results for machine learning (SVM, k-NN), and reduce noise.

6. Limitations and conclusion

SVD turns out to be a useful and an universal tool from linear algebra, and can provide a sound, robust tool set to analyze and manipulate matrixes. As a result SVD will allow us to decompose a matrix into orthogonal and diagonal components and to give a geom SD interpretation of linear transformations and characterise linear transformations (rank, nullity, principal directions of variation). The application of eigenvalue decomposition is permitted only to square matrices, and their extensions, whereas SVD can be applied to any matrices (square, nonsquare, symmetric or asymmetric) and is therefore very convenient to use in modern computational mathematics. The Singular Value Decomposition (SVD) exhibits remarkable practicality, finding applications in diverse domains such as image compression, noise reduction, data analysis, and dimensionality reduction. Python-based implementations have demonstrated that SVD can effectively reduce the dimensionality of high-dimensional data while preserving a substantial amount of information, minimizing significant information loss. It is concluded that SVD is central to numerical linear algebra and to data science, and provides an efficient way to obtain solutions to difficult engineering, machine learning, and scientific computing problems. This approach is likely to remain relevant in the world, where there’s big data processing, as it can identify meaningful patterns of the data and is stable in computing. This demonstrates that the advancements will make the use and efficacy of SVD applicable and efficient in new fields.

Singular Value Decomposition (SVD) is a powerful technique to solve matrix problems but is computationally expensive (O(min(mn², m²n)) complexity), noisy and memory constraint for large datasets[9][10]. In addition, it does not work well with nonlinear structures. Several aspects of future research regarding scalable SVD using parallel and randomized methods and robust variants that are resistant to noise remain for future investigate. Other nonlinear extraction approaches (integration with deep learning) can be combined with adaptive rank selection techniques to determine the superior dimensionality reduction. The applications of quantum SVD include large scale computations and could be federated learning and biomedical signal processing. The appropriate of these limitations will enhance SVD’s efficiency and will extend its reach in information technology and data science.